Реализация запроса в дереве отрезков сверху — различия между версиями
Shagal (обсуждение | вклад) |
Shagal (обсуждение | вклад) (→Пример) |
||
| Строка 9: | Строка 9: | ||
==Пример== | ==Пример== | ||
| − | [[Файл: | + | [[Файл:Шагал1538.JPG|right|380px|thumb|Дерево отрезков]] |
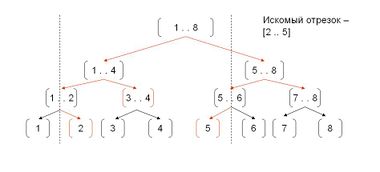
Рассмотрим работу программы на дереве отрезков для элементов [1 .. 8]. | Рассмотрим работу программы на дереве отрезков для элементов [1 .. 8]. | ||
| Строка 24: | Строка 24: | ||
| − | 4)лист 6 не пересекается с отрезком [2 .. 5] => возвращаем нулевое значение, лист 5 целиков внутри [2 .. 5] => возвращаем значение в листе 5. | + | 4)лист 6 не пересекается с отрезком [2 .. 5] => возвращаем нулевое значение, лист 5 целиков внутри [2 .. 5] => возвращаем значение в листе 5. |
| − | |||
==Реализация== | ==Реализация== | ||
Версия 22:49, 16 мая 2011
Содержание
Алгоритм
Будем рассматривать запрос на примере задачи RSQ(запрос суммы)
Если запрашиваемый отрезок не пересекается с рассматриваемым отрезком, возвращаем нейтральный элемент. Если запрашиваемый отразив совпадает с запрашиваемый, возвращаем значение в вершине. Иначе считаем для подотрезков рекурсивно, комбинируем ответ и возвращаем значение.
Пример
Рассмотрим работу программы на дереве отрезков для элементов [1 .. 8]. Пусть запрашиваемая сумма - это отрезок [2 .. 5].
1)Текущий отрезок [1 .. 8], он больше [2 .. 5] => переходим по рекурсивным вызовам на [1 .. 4] и [5 .. 8]
2)[1 .. 4] выходит за границы [2 .. 5], [5 .. 8] выходит за границы [2 .. 5] => переходим по рекурсивным вызовам на [1 .. 2], [3 .. 4] и [5 .. 6], [7 .. 8].
3)[1 .. 2] выходит за границы [2 .. 5] => переходим в листья 1, 2; [3 .. 4] целиком внутри [2 .. 5] => возвращаем значение в [3 .. 4];
[7 .. 8] не пересекается с [2 .. 5] => возвращаем нулевое значение, [5 .. 6] выходит за границы [2 .. 5] => переходим к листьям 5 и 6
4)лист 6 не пересекается с отрезком [2 .. 5] => возвращаем нулевое значение, лист 5 целиков внутри [2 .. 5] => возвращаем значение в листе 5.
Реализация
int sum (int v, int tl, int tr, int l, int r)
{
if ([l,r] не пересекается с [tl, tr])
return 0;
if (l == tl && r == tr)
return t[v];
int tm = (tl + tr) / 2;
return sum (v*2, tl, tm, l, min(r,tm))
+ sum (v*2+1, tm+1, tr, max(l,tm+1), r);
}