Реализация запроса в дереве отрезков сверху — различия между версиями
Shagal (обсуждение | вклад) (→Пример) |
Shagal (обсуждение | вклад) (→Алгоритм) |
||
| Строка 3: | Строка 3: | ||
[[Файл:123.jpg|right|380px|thumb|Пример дерева отрезков для вычисления сумм]] | [[Файл:123.jpg|right|380px|thumb|Пример дерева отрезков для вычисления сумм]] | ||
| − | Пусть есть дерево отрезков и задача найти сумму на отрезке [a .. b], далее искомый. | + | Пусть есть дерево отрезков и задача найти сумму на отрезке <tex>[a .. b]</tex>, далее искомый. |
Запустим рекурсивную процедуру от всего отрезка. | Запустим рекурсивную процедуру от всего отрезка. | ||
| Строка 12: | Строка 12: | ||
Например: | Например: | ||
| − | текущий [1..2], а искомый [3 .. 4]; | + | текущий <tex>[1..2]</tex>, а искомый <tex>[3 .. 4]</tex>; |
*текущий отрезок целиком внутри, то возвращаем значение в вершине. | *текущий отрезок целиком внутри, то возвращаем значение в вершине. | ||
Например: | Например: | ||
| − | текущий [2..3], а искомый [1 .. 4]; | + | текущий <tex>[2..3]</tex>, а искомый <tex>[1 .. 4]</tex>; |
Далее переходим к рекурсивным вызовам | Далее переходим к рекурсивным вызовам | ||
Версия 23:31, 16 мая 2011
Содержание
Алгоритм
Будем рассматривать запрос на примере задачи RSQ(запрос суммы)
Пусть есть дерево отрезков и задача найти сумму на отрезке , далее искомый.
Запустим рекурсивную процедуру от всего отрезка.
Проверять будем два условия :
- если текущий отрезок не пересекается с искомым, то возвращаем нулевое значение.
Например:
текущий , а искомый ;
- текущий отрезок целиком внутри, то возвращаем значение в вершине.
Например:
текущий , а искомый ;
Далее переходим к рекурсивным вызовам результат функции от текущего отрезка и искомого = сумма результатов от детей текущего отрезка и искомого.
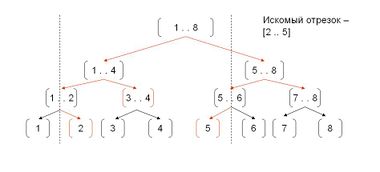
Пример
Рассмотрим работу программы на дереве отрезков для элементов . Пусть запрашиваемая сумма - это отрезок .
- Текущий отрезок , он больше => переходим по рекурсивным вызовам на и
- выходит за границы, выходит за границы => переходим по рекурсивным вызовам на , и , .
- выходит за границы => переходим в листья 1, 2; целиком внутри => возвращаем значение в ;
не пересекается с => возвращаем нулевое значение, выходит за границы => переходим к листьям 5 и 6
- лист 6 не пересекается с отрезком => возвращаем нулевое значение, лист 5 целиков внутри => возвращаем значение в листе 5.
Реализация
int sum (int v, int tl, int tr, int l, int r)
{
if ([l,r] [tl, tr]) =
return 0;
if ([l,r] [tl, tr])
return t[v];
int tm = (tl + tr) / 2;
return sum (v*2, tl, tm, l, min(r,tm))
+ sum (v*2+1, tm+1, tr, max(l,tm+1), r);
}