О замене переменной в интеграле многих переменных — различия между версиями
Sementry (обсуждение | вклад) м (до теоремы о замене переменных в двойном интеграле от произвольной функции) |
Sementry (обсуждение | вклад) |
||
| Строка 128: | Строка 128: | ||
<Сюда можно впилить долгий монолог о сложности понятия площади поверхности> | <Сюда можно впилить долгий монолог о сложности понятия площади поверхности> | ||
| + | {{Теорема | ||
| + | |about= | ||
| + | Замена переменных интегрирования в двойном интеграле | ||
| + | |statement= | ||
| + | Пусть дан закон преобразования переменных, | ||
$\begin{cases} | $\begin{cases} | ||
x & = x(u, v)\\ | x & = x(u, v)\\ | ||
y & = y(u, v)\\ | y & = y(u, v)\\ | ||
| − | \end{cases}$ | + | \end{cases}$; |
| + | $E$ - квадрируемая фигура в $Oxy$, якобиан преобразования определен так же, как и ранее. Пусть $f: E \rightarrow \mathbb R$. Тогда выполняется $|E| = \iint\limits_{E}f(x, y)dxdy = \iint\limits_{E'}f(x(u, v), y(u, v))|J(u, v)|dudv $ | ||
| + | |proof= | ||
| + | Если всё делать строго, мы утонем в некоторой дифференицальной геометрии. Будем всё делать нестрого. | ||
| − | + | Покроем плоскость сетью координатных линий с малыми шагами, в результате $E$ будет разбиваться на части элементарными криволинейными параллелограммами. | |
| − | $\ | + | Перейдем к образу: |
| + | |||
| + | КАРТИНКА КАРТИНКА[переход к образу, все так же, как и для фигуры Е ранее] | ||
| + | |||
| + | Каждая прямоугольная клетка справа является образом элементарного криволинейного параллелограмма слева. | ||
| + | |||
| + | $E$ - квадрируема, значит, сумма площадей параллелограммов(а в образе - прямоугольников) на границе будет сколь угодно малой при устремлении ранга разбиения к нулю. Значит, можно принебречь суммой этих групп слагаемых в соответствующих интегральных суммах. | ||
| + | |||
| + | Рассмотрим кусочек интегральной суммы, $f(p_i)|E_i|$, $p_i = (x_i, y_i)$. Как мы ранее установили, $|E_i| = \iint\limits{E_i'}|J(u, v)|dudv$. | ||
| + | |||
| + | Пусть точка $p_i'$ - образ $p_i$, для интегральной суммы образа получаем: | ||
| + | |||
| + | $S = f(x(u_i, v_i), y(u_i, v_i)) |J(u_i, v_i)|\Delta u_i \Delta v_i$. | ||
| + | |||
| + | Сравним с исходной площадью: | ||
| + | |||
| + | $\left| f(x_i, y_i)|E_i| - f(x(u_i, v_i), y(u_i, v_i)) |J(u_i, v_i)|\Delta u_i \Delta v_i \right| =$ | ||
| + | |||
| + | $= f(x_i, y_i) \left| |E_i| = \iint\limits{E_i'}|J(u, v)|dudv - |J(u_i, v_i)|\Delta u_i \Delta v_i \right| \le$ | ||
| + | |||
| + | (так как при $\operatorname{rang} \tau < \delta, \forall E_i: \left| |J(u, v)| - |J(u_i, v_i)| \right| < \varepsilon$, а $\Delta u_i \Delta v_i = \iint\limits{E_i'}dudv$) | ||
| + | |||
| + | $\le f(x_i, y_i) \iint\limits{E_i'} \left| |J(u, v)| - |J(u_i, v_i)| \right|dudv \le$ | ||
| + | |||
| + | (тут пара каких-то очень мутных переходов) | ||
| + | |||
| + | $\le \varepsilon |E'|$ | ||
| + | |||
| + | Это выполняется для любого $\varepsilon > 0$, значит, теорема доказана. | ||
| + | }} | ||
| + | |||
| + | Далее будет доказана более общая и крутая теорема Фубини, которая более строго ответит на наши вопросы. | ||
</wikitex> | </wikitex> | ||
Версия 08:35, 13 июня 2011
Как обычно, будем рассматривать функцию двух переменных.
[Тут какое-то невнятно написанное предложение про мотивацию]
Площадь сектора . Пусть эта формула нам известна. (рис 1)
КАРТИНКА КАРТИНКА[Окружности радиуса и с общим центром. Также нарисован угол , площать - площадь сегмента, окраниченного двумя окружностями и углом.]
,
Или, .
Рассмотрим полярные координаты.
Рассмотрим линии уровня. — ГМТ, для каждой из которых значение радиуса одно и то же и равно . Аналогично, — ГМТ, для каждой из которых
Меняя в и и , покрываем плоскость сетью окружностей и лучей.
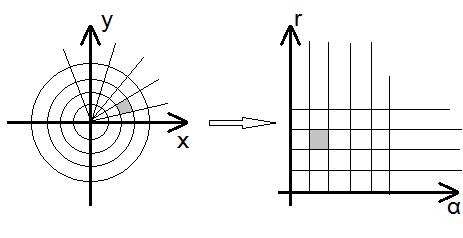
Если на написанную систему соотношений смотреть как на преобразование плоскости и смотреть образы и , в силу их определений это будет сеть вертикалей и горизонталей.
Если заштриховать фигуру, границы которой — эти линии, то её образ будет прямоугольником. При обозначении его площади за получаем предел выше. Тогда этот предел — коэффициент искажения элементарной площади при переходе из одной системы осей в другую.
Прямоугольник под действим переходит в , причём ().
Итак, первый этап завершён. Найдена плотность(коэффициент искажения).
На втором этапе мы заинтегрируем эту плотность и придём к формуле , которая будет базовой формулой для того, что бы научиться заменять переменные в двойных интегралах.
Будем считать, что мы знаем, что если есть , — образ, то , где . Это стремление равномерно по положению точки в пределах прямоугольника. (рис 5)
КАРТИНКА[ преобразованием T переходит в ]
Рассмотрим квадрируемую фигуру . ,
, где — бесконечно малое.
По равномерной непрерывности, при , .
Тогда первое слагаемое — интегральная сумма, а второе стремится к нулю. Тогда
Пример. КАРТИНКА[Круг под действием преобразования переходит в прямоугольник.]
Плошадь круга.
Общий случай
<wikitex> Пусть $\begin{cases} x & = x(u, v)\\ y & = y(u, v)\\ \end{cases}$;
где $(x, y)$ — прямоугольные координаты, $(u, v)$ — криволинейные.
$l_u$, $l_v$ — линии уровня(координатные линии) в $OXY$.
КАРТИНКА КАРТИНКА[Кривые линии уровня и переход их под действием преобразования в стандартные линии уровня для плоскости.]
Рассмотрим элементарную клетку получвшейся криволинейной сети.
КАРТИНКА КАРТИНКА[в безобразии из предыдущей пары картинок рассматриваем элементарную клетку $E_{uv}$, зажатую между соседними линиями]
В $OXY$ элементарная клетка — прямоугольник.
$\frac{|E_{uv}|}{E'_{uv}} = \frac{|E_{uv}|}{\Delta u\Delta v}$
Соединим отрезками вершины клетки, получим четырёхугольник, который примерно параллелограмм, и вычислим его площадь.
Можно действовать по-другому: построить касательные к линиям уровня в точках пересечения, нормировать их, получить паралелограмм и считать его площадь.
Эти попытки связаны с тем, что хочется понять, что будет аналогом $R$ в полярных координатах.
$\overline K_u = (x_v'; y_v')$ — касательный вектор к линии уровня $l_u$
$\overline K_v = (x_u'; y_u')$ — касательный вектор к линии уровня $l_v$
$K_u\Delta v, K_v\Delta u$ - элементарные приращения, приблизительно образующие $E_{uv}$. Построим на них параллелограмм, его площадь:
$P(u, v) = \begin{pmatrix} x_u' & y_u' \\ x_v' & y_v' \\ \end{pmatrix} $
$J(u, v) = det(P(u, v))$;
$ S = |J(u, v)|\Delta u \Delta v$.
Для $p \in E_p$, $\frac{|E_p|}{|E_p'|} \xrightarrow[diam p \rightarrow 0]{}{|J(u, v)|}$, получившийся предел называется якобианом преобразования.
В итоге получаем $|E| = \iint\limits_{E}dxdy = \iint\limits_{E'}|J(u, v)|dudv$
<Сюда можно впилить долгий монолог о сложности понятия площади поверхности>
| Теорема (Замена переменных интегрирования в двойном интеграле): |
Пусть дан закон преобразования переменных,
$\begin{cases} x & = x(u, v)\\ y & = y(u, v)\\ \end{cases}$; $E$ - квадрируемая фигура в $Oxy$, якобиан преобразования определен так же, как и ранее. Пусть $f: E \rightarrow \mathbb R$. Тогда выполняется $ |
| Доказательство: |
|
Если всё делать строго, мы утонем в некоторой дифференицальной геометрии. Будем всё делать нестрого. Покроем плоскость сетью координатных линий с малыми шагами, в результате $E$ будет разбиваться на части элементарными криволинейными параллелограммами. Перейдем к образу: КАРТИНКА КАРТИНКА[переход к образу, все так же, как и для фигуры Е ранее] Каждая прямоугольная клетка справа является образом элементарного криволинейного параллелограмма слева. $E$ - квадрируема, значит, сумма площадей параллелограммов(а в образе - прямоугольников) на границе будет сколь угодно малой при устремлении ранга разбиения к нулю. Значит, можно принебречь суммой этих групп слагаемых в соответствующих интегральных суммах. Рассмотрим кусочек интегральной суммы, $f(p_i) |
Далее будет доказана более общая и крутая теорема Фубини, которая более строго ответит на наши вопросы. </wikitex>