Декартово дерево — различия между версиями
(→Реализация №1:) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 213 промежуточных версий 23 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | ''Эта статья про курево'' |
| − | + | '''Декартово дерево или дерамида''' (англ. ''Treap'') {{---}} это структура данных, объединяющая в себе [[Дерево поиска, наивная реализация|бинарное дерево поиска]] и [[Двоичная куча|бинарную кучу]] (отсюда и второе её название: treap (tree + heap) и дерамида (дерево + пирамида), также существует название курево (куча + дерево). | |
| − | + | Более строго, это бинарное дерево, в узлах которого хранятся пары <tex> (x,y) </tex>, где <tex>x</tex> {{---}} это ключ, а <tex>y</tex> {{---}} это приоритет. Также оно является двоичным деревом поиска по <tex>x</tex> и пирамидой по <tex>y</tex>. Предполагая, что все <tex>x</tex> и все <tex>y</tex> являются различными, получаем, что если некоторый элемент дерева содержит <tex>(x_0,y_0)</tex>, то у всех элементов в левом поддереве <tex>x < x_0</tex>, у всех элементов в правом поддереве <tex> x > x_0</tex>, а также и в левом, и в правом поддереве имеем: <tex> y < y_0</tex>. | |
| − | |||
| − | + | Дерамиды были предложены Сиделем (Siedel) и Арагон (Aragon) в 1996 г. | |
| − | == | + | == Операции в декартовом дереве == |
| + | === split === | ||
| + | [[file:split.png|thumb|400px|Операция split]] | ||
| − | + | Операция <tex>\mathrm{split}</tex> (''разрезать'') позволяет сделать следующее: разрезать исходное дерево <tex>T</tex> по ключу <tex>k</tex>. Возвращать она будет такую пару деревьев <tex>\langle T_1, T_2\rangle </tex>, что в дереве <tex>T_1</tex> ключи меньше <tex>k</tex>, а в дереве <tex>T_2</tex> все остальные: <tex>\mathrm{split}(T, k) \to \langle T_1, T_2\rangle </tex>. | |
| − | + | Эта операция устроена следующим образом. | |
| − | |||
| − | + | Рассмотрим случай, в котором требуется разрезать дерево по ключу, большему ключа корня. | |
| − | + | Посмотрим, как будут устроены результирующие деревья <tex>T_1</tex> и <tex>T_2</tex>: | |
| − | < | + | * <tex>T_1</tex>: левое поддерево <tex>T_1</tex> совпадёт с левым поддеревом <tex>T</tex>. Для нахождения правого поддерева <tex>T_1</tex>, нужно разрезать правое поддерево <tex>T</tex> на <tex>T^R_1</tex> и <tex>T^R_2</tex> по ключу <tex>k</tex> и взять <tex>T^R_1</tex>. |
| − | < | + | * <tex>T_2</tex> совпадёт с <tex>T^R_2</tex>. |
| + | Случай, в котором требуется разрезать дерево по ключу, меньше либо равному ключа в корне, рассматривается симметрично. | ||
| − | === | + | === Псевдокод === |
| − | |||
| + | '''<tex>\langle</tex>Treap, Treap<tex>\rangle</tex>''' split(t: '''Treap''', k: '''int'''): | ||
| + | '''if''' t == <tex> \varnothing </tex> | ||
| + | '''return''' <tex>\langle</tex><tex> \varnothing </tex>, <tex> \varnothing </tex><tex>\rangle</tex> | ||
| + | '''else if''' k > t.x | ||
| + | <tex>\langle</tex>t1, t2<tex>\rangle</tex> = split(t.right, k) | ||
| + | t.right = t1 | ||
| + | '''return''' <tex>\langle</tex>t, t2<tex>\rangle</tex> | ||
| + | '''else''' | ||
| + | <tex>\langle</tex>t1, t2<tex>\rangle</tex> = split(t.left, k) | ||
| + | t.left = t2 | ||
| + | '''return''' <tex>\langle</tex>t1, t<tex>\rangle</tex> | ||
| − | == | + | === Время работы === |
| − | |||
| − | + | Оценим время работы операции <tex>\mathrm{split}</tex>. Во время выполнения вызывается одна операция <tex>\mathrm{split}</tex> для | |
| − | + | дерева хотя бы на один меньшей высоты и делается ещё <tex>O(1)</tex> операций. Тогда итоговая трудоёмкость этой операции | |
| − | + | равна <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. | |
| − | |||
| − | ===Реализация №2 | + | === merge === |
| − | Спускаемся по дереву (как в обычном бинарном дереве поиска по <tex> | + | [[file:merge.png|thumb|400px|Операция merge]] |
| + | |||
| + | Рассмотрим вторую операцию с декартовыми деревьями {{---}} <tex>\mathrm{merge}</tex> (''слить''). | ||
| + | |||
| + | С помощью этой операции можно слить два декартовых дерева в одно. | ||
| + | Причём, все ключи в первом(''левом'') дереве должны быть меньше, чем | ||
| + | ключи во втором(''правом''). В результате получается дерево, в котором есть все ключи из первого и второго деревьев: <tex>\mathrm{merge}(T_1, T_2) \to \{T\}</tex> | ||
| + | |||
| + | Рассмотрим принцип работы этой операции. Пусть нужно слить деревья <tex>T_1</tex> и <tex>T_2</tex>. | ||
| + | Тогда, очевидно, у результирующего дерева <tex>T</tex> есть корень. | ||
| + | Корнем станет вершина из <tex>T_1</tex> или <tex>T_2</tex> с наибольшим приоритетом <tex>y</tex>. Но вершина с самым большим <tex>y</tex> из всех вершин деревьев | ||
| + | <tex>T_1</tex> и <tex>T_2</tex> может быть только либо корнем <tex>T_1</tex>, либо корнем <tex>T_2</tex>. | ||
| + | Рассмотрим случай, в котором корень <tex>T_1</tex> имеет больший <tex>y</tex>, чем корень <tex>T_2</tex>. | ||
| + | Случай, в котором корень <tex>T_2</tex> имеет больший <tex>y</tex>, чем корень <tex>T_1</tex>, симметричен этому. | ||
| + | |||
| + | Если <tex>y</tex> корня <tex>T_1</tex> больше <tex>y</tex> корня <tex>T_2</tex>, то он и будет являться корнем. Тогда левое поддерево | ||
| + | <tex>T</tex> совпадёт с левым поддеревом <tex>T_1</tex>. Справа же нужно подвесить объединение правого поддерева | ||
| + | <tex>T_1</tex> и дерева <tex>T_2</tex>. | ||
| + | |||
| + | === Псевдокод === | ||
| + | |||
| + | '''Treap''' merge(t1: '''Treap''', t2: '''Treap'''): | ||
| + | '''if''' t2 == <tex> \varnothing </tex> | ||
| + | '''return''' t1 | ||
| + | '''if''' t1 == <tex> \varnothing </tex> | ||
| + | '''return''' t2 | ||
| + | '''else if''' t1.y > t2.y | ||
| + | t1.right = merge(t1.right, t2) | ||
| + | '''return''' t1 | ||
| + | '''else''' | ||
| + | t2.left = merge(t1, t2.left) | ||
| + | '''return''' t2 | ||
| + | |||
| + | === Время работы === | ||
| + | |||
| + | Рассуждая аналогично операции <tex>\mathrm{split}</tex>, приходим к выводу, что трудоёмкость операции <tex>\mathrm{merge}</tex> | ||
| + | равна <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева. | ||
| + | |||
| + | === insert === | ||
| + | Операция <tex>\mathrm{insert}(T, k)</tex> добавляет в дерево <tex>T</tex> элемент <tex>k</tex>, где <tex>k.x</tex> {{---}} ключ, а <tex>k.y</tex> {{---}} приоритет. | ||
| + | |||
| + | Представим что элемент <tex>k</tex>, это декартово дерево из одного элемента, и для того чтобы его добавить в наше декартово дерево <tex>T</tex>, очевидно, нам нужно их слить. Но <tex>T</tex> может содержать ключи как меньше, так и больше ключа <tex>k.x</tex>, поэтому сначала нужно разрезать <tex>T</tex> по ключу <tex>k.x</tex>. | ||
| + | |||
| + | * Реализация №1 | ||
| + | # Разобьём наше дерево по ключу, который мы хотим добавить, то есть <tex>\mathrm{split}(T, k.x) \to \langle T_1, T_2\rangle</tex>. | ||
| + | # Сливаем первое дерево с новым элементом, то есть <tex>\mathrm{merge}(T_1, k) \to T_1</tex>. | ||
| + | # Сливаем получившиеся дерево со вторым, то есть <tex>\mathrm{merge}(T_1, T_2) \to T</tex>. | ||
| + | |||
| + | * Реализация №2 | ||
| + | # Сначала спускаемся по дереву (как в обычном бинарном дереве поиска по <tex>k.x</tex>), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше <tex>k.y</tex>. | ||
| + | # Теперь вызываем <tex>\mathrm{split}(T, k.x) \to \langle T_1, T_2\rangle</tex> от найденного элемента (от элемента вместе со всем его поддеревом) | ||
| + | # Полученные <tex>T_1</tex> и <tex>T_2</tex> записываем в качестве левого и правого сына добавляемого элемента. | ||
| + | # Полученное дерево ставим на место элемента, найденного в первом пункте. | ||
| + | |||
| + | В первой реализации два раза используется <tex>\mathrm{merge}</tex>, а во второй реализации слияние вообще не используется. | ||
| + | |||
| + | === remove === | ||
| + | Операция <tex>\mathrm{remove}(T, x)</tex> удаляет из дерева <tex>T</tex> элемент с ключом <tex>x</tex>. | ||
| + | |||
| + | * Реализация №1 | ||
| + | |||
| + | # Разобьём наше дерево по ключу, который мы хотим удалить, то есть <tex>\mathrm{split }(T, k.x) \to \langle T_1, T_2\rangle</tex>. | ||
| + | # Теперь отделяем от первого дерева элемент <tex>x</tex>, то есть самого левого ребёнка дерева <tex> T_2 </tex>. | ||
| + | # Сливаем первое дерево со вторым, то есть <tex>\mathrm{merge }(T_1, T_2) \to T</tex>. | ||
| + | |||
| + | * Реализация №2 | ||
| + | # Спускаемся по дереву (как в обычном бинарном дереве поиска по <tex>x</tex>), и ищем удаляемый элемент. | ||
| + | # Найдя элемент, вызываем <tex>\mathrm{merge}</tex> его левого и правого сыновей | ||
| + | # Результат процедуры <tex>\mathrm{merge}</tex> ставим на место удаляемого элемента. | ||
| + | |||
| + | В первой реализации один раз используется <tex>\mathrm{split}</tex>, а во второй реализации разрезание вообще не используется. | ||
| + | |||
| + | == Построение декартова дерева == | ||
| + | Пусть нам известно из каких пар <tex>(x_i, y_i)</tex> требуется построить декартово дерево, причём также известно, что <tex>x_1 < x_2 < \ldots < x_n</tex>. | ||
| + | === Алгоритм за <tex>O(n\log n)</tex> === | ||
| + | Отсортируем все приоритеты по убыванию за <tex> O(n\log n) </tex> и выберем первый из них, пусть это будет <tex>y_k</tex>. Сделаем <tex>(x_k, y_k)</tex> корнем дерева. Проделав то же самое с остальными вершинами получим левого и правого сына <tex>(x_k, y_k)</tex>. В среднем высота Декартова дерева <tex>\log n</tex> (см. далее) и на каждом уровне мы сделали <tex>O(n)</tex> операций. Значит такой алгоритм работает за <tex>O(n\log n)</tex>. | ||
| + | |||
| + | |||
| + | === Другой алгоритм за <tex>O(n\log n)</tex> === | ||
| + | Отсортируем пары <tex>(x_i, y_i)</tex> по убыванию <tex>x_i</tex> и положим их в очередь. Сперва достанем из очереди первые <tex>2</tex> элемента и сольём их в дерево и положим в конец очереди, затем сделаем то же самое со следующими двумя и т.д. Таким образом, мы сольём сначала <tex>n</tex> деревьев размера <tex>1</tex>, затем <tex>\dfrac{n}{2}</tex> деревьев размера <tex>2</tex> и так далее. При этом на уменьшение размера очереди в два раза мы будем тратить суммарно <tex>O(n)</tex> время на слияния, а всего таких уменьшений будет <tex>\log n</tex>. Значит полное время работы алгоритма будет <tex>O(n\log n)</tex>. | ||
| + | |||
| + | === Алгоритм за <tex>O(n)</tex> === | ||
| + | Будем строить дерево слева направо, то есть начиная с <tex>(x_1, y_1)</tex> по <tex>(x_n, y_n)</tex>, при этом помнить последний добавленный элемент <tex>(x_k, y_k)</tex>. Он будет самым правым, так как у него будет максимальный ключ, а по ключам декартово дерево представляет собой [[Дерево поиска, наивная реализация|двоичное дерево поиска]]. При добавлении <tex>(x_{k+1}, y_{k+1})</tex>, пытаемся сделать его правым сыном <tex>(x_k, y_k)</tex>, это следует сделать если <tex>y_k > y_{k+1}</tex>, иначе делаем шаг к предку последнего элемента и смотрим его значение <tex>y</tex>. Поднимаемся до тех пор, пока приоритет в рассматриваемом элементе меньше приоритета в добавляемом, после чего делаем <tex>(x_{k+1}, y_{k+1})</tex> его правым сыном, а предыдущего правого сына делаем левым сыном <tex>(x_{k+1}, y_{k+1})</tex>. | ||
| + | |||
| + | |||
| + | Заметим, что каждую вершину мы посетим максимум дважды: при непосредственном добавлении и, поднимаясь вверх (ведь после этого вершина будет лежать в чьём-то левом поддереве, а мы поднимаемся только по правому). Из этого следует, что построение происходит за <tex>O(n)</tex>. | ||
| + | |||
| + | == Случайные приоритеты == | ||
| + | Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей <tex>(1, 1), \ldots, (n, n)</tex>, будет равна <tex>n</tex>. Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно. | ||
| + | |||
| + | == Высота в декартовом дереве с случайными приоритетами == | ||
| + | {{Теорема | ||
| + | |statement = В декартовом дереве из <tex>n</tex> узлов, приоритеты <tex>y</tex> которого являются [[Дискретная случайная величина|случайными величинами]] c равномерным распределением, средняя глубина вершины <tex>O(\log n)</tex>. | ||
| + | |proof= | ||
| + | |||
| + | Будем считать, что все выбранные приоритеты <tex>y</tex> попарно различны. | ||
| + | |||
| + | Для начала введём несколько обозначений: | ||
| + | * <tex>x_k</tex> {{---}} вершина с <tex>k</tex>-ым по величине ключом; | ||
| + | * индикаторная величина <tex>A_{i, j} = \left\{\begin{array}{lllc} 1 ,&& x_i\ \text{is ancestor of} \ x_j\\ | ||
| + | 0 ,&& \text{otherwise}\\ | ||
| + | \end{array}\right. | ||
| + | </tex> | ||
| + | * <tex>d(v)</tex> {{---}} глубина вершины <tex>v</tex>; | ||
| + | |||
| + | В силу обозначений глубину вершины можно записать как количество предков: | ||
| + | :<tex>d(x_k) = \sum\limits_{i = 1}^{n} A_{i,k} </tex>. | ||
| + | |||
| + | Теперь можно выразить [[Математическое ожидание случайной величины|математическое ожидание]] глубины конкретной вершины: | ||
| + | :<tex>E(d(x_k)) = \sum\limits_{i = 1}^{n} Pr[A_{i,k} = 1] </tex> {{---}} здесь мы использовали линейность математического ожидания, и то что <tex>E(X) = Pr[X = 1]</tex> для индикаторной величины <tex>X</tex> (<tex>Pr[A]</tex> {{---}} вероятность события <tex>A</tex>). | ||
| + | Для подсчёта средней глубины вершин нам нужно сосчитать вероятность того, что вершина <tex>x_i</tex> является предком вершины <tex>x_k</tex>, то есть <tex>Pr[A_{i,k} = 1]</tex>. | ||
| + | |||
| + | Введём новое обозначение: | ||
| + | * <tex>X_{i, k}</tex> {{---}} множество ключей <tex>\{x_i, \ldots, x_k\}</tex> или <tex>\{x_k, \ldots, x_i\}</tex>, в зависимости от <tex>i < k</tex> или <tex>i > k</tex>. <tex>X_{i, k}</tex> и <tex>X_{k, i}</tex> обозначают одно и тоже, их мощность равна <tex>|k - i| + 1</tex>. | ||
| + | |||
| + | {{Лемма | ||
| + | |statement=Для любых <tex>i \ne k</tex> , <tex>x_i</tex> является предком <tex>x_k</tex> тогда и только тогда, когда <tex>x_i</tex> имеет наибольший приоритет среди <tex>X_{i, k}</tex>. | ||
| + | |proof=Если <tex>x_i</tex> является корнем, то оно является предком <tex>x_k</tex> и по определению имеет максимальный приоритет среди всех вершин, следовательно, и среди <tex>X_{i, k}</tex>. | ||
| + | |||
| + | С другой стороны, если <tex>x_k</tex> {{---}} корень, то <tex>x_i</tex> {{---}} не предок <tex>x_k</tex>, и <tex>x_k</tex> имеет максимальный приоритет в декартовом дереве; следовательно, <tex>x_i</tex> не имеет наибольший приоритет среди <tex>X_{i, k}</tex>. | ||
| + | |||
| + | Теперь предположим, что какая-то другая вершина <tex>x_m</tex> {{---}} корень. Тогда, если <tex>x_i</tex> и <tex>x_k</tex> лежат в разных поддеревьях, то <tex>i < m < k</tex> или <tex>i > m > k</tex>, следовательно, <tex>x_m</tex> содержится в <tex>X_{i , k}</tex>. В этом случае <tex>x_i</tex> {{---}} не предок <tex>x_k</tex>, и наибольший приоритет среди <tex>X_{i, k}</tex> имеет вершина с номером <tex>m</tex>. | ||
| + | |||
| + | Наконец, если <tex>x_i</tex> и <tex>x_k</tex> лежат в одном поддереве, то доказательство применяется по индукции: пустое декартово дерево есть тривиальная база, а рассматриваемое поддерево является меньшим декартовым деревом. | ||
| + | }} | ||
| + | |||
| + | Так как распределение приоритетов равномерное, каждая вершина среди <tex>X_{i, k}</tex> может иметь максимальный приоритет, мы немедленно приходим к следующему равенству: | ||
| + | : <tex>Pr[A_{i, k} = 1] = \left\{\begin{array}{lllc} \dfrac{1}{k - i + 1} ,&& k \ > \ i\\ | ||
| + | 0 ,&& k\ =\ i\\ | ||
| + | \dfrac{1}{i - k + 1} ,&& k \ < \ i\\ | ||
| + | \end{array}\right. | ||
| + | </tex> | ||
| + | |||
| + | Подставив последнее в нашу формулу с математическим ожиданием получим: | ||
| + | :<tex>E(d(x_k)) = \sum\limits_{i = 1}^{n} Pr[A_{i,k} = 1] = \sum\limits_{i = 1}^{k - 1}\dfrac{1}{k - i + 1} + \sum\limits_{i = k + 1}^{n}\dfrac{1}{i - k + 1} \leqslant </tex> | ||
| + | <tex>\leqslant \ln(k) + \ln(n - k)+2</tex> (здесь мы использовали неравенство <tex>\sum\limits_{i = 1}^{n} \dfrac{1}{i} \leqslant \ln(n) + 1</tex>) | ||
| + | : <tex>\log(n)</tex> отличается от <tex>\ln(n)</tex> в константу раз, поэтому <tex>\log(n) = O(\ln(n))</tex>. | ||
| + | |||
| + | В итоге мы получили что <tex>E(d(x_k)) = O(\log(n))</tex>. | ||
| + | }} | ||
| + | |||
| + | Таким образом, среднее время работы операций <tex>\mathrm{split}</tex> и <tex>\mathrm{merge}</tex> будет <tex>O(\log(n))</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Декартово дерево по неявному ключу]] | ||
| + | |||
| + | == Источники информации == | ||
| + | *[http://ru.wikipedia.org/wiki/Декартово_дерево Декартово дерево — Википедия] | ||
| + | *[http://rain.ifmo.ru/cat/data/theory/trees/treaps-2006/article.pdf Treaps и T-Treaps] | ||
| + | |||
| + | [[Категория:Дискретная математика и алгоритмы]] | ||
| + | [[Категория:Деревья поиска]] | ||
Текущая версия на 19:35, 4 сентября 2022
Эта статья про курево
Декартово дерево или дерамида (англ. Treap) — это структура данных, объединяющая в себе бинарное дерево поиска и бинарную кучу (отсюда и второе её название: treap (tree + heap) и дерамида (дерево + пирамида), также существует название курево (куча + дерево).
Более строго, это бинарное дерево, в узлах которого хранятся пары , где — это ключ, а — это приоритет. Также оно является двоичным деревом поиска по и пирамидой по . Предполагая, что все и все являются различными, получаем, что если некоторый элемент дерева содержит , то у всех элементов в левом поддереве , у всех элементов в правом поддереве , а также и в левом, и в правом поддереве имеем: .
Дерамиды были предложены Сиделем (Siedel) и Арагон (Aragon) в 1996 г.
Содержание
Операции в декартовом дереве
split
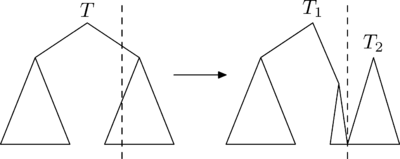
Операция (разрезать) позволяет сделать следующее: разрезать исходное дерево по ключу . Возвращать она будет такую пару деревьев , что в дереве ключи меньше , а в дереве все остальные: .
Эта операция устроена следующим образом.
Рассмотрим случай, в котором требуется разрезать дерево по ключу, большему ключа корня. Посмотрим, как будут устроены результирующие деревья и :
- : левое поддерево совпадёт с левым поддеревом . Для нахождения правого поддерева , нужно разрезать правое поддерево на и по ключу и взять .
- совпадёт с .
Случай, в котором требуется разрезать дерево по ключу, меньше либо равному ключа в корне, рассматривается симметрично.
Псевдокод
Treap, Treap split(t: Treap, k: int): if t == return , else if k > t.x t1, t2 = split(t.right, k) t.right = t1 return t, t2 else t1, t2 = split(t.left, k) t.left = t2 return t1, t
Время работы
Оценим время работы операции . Во время выполнения вызывается одна операция для дерева хотя бы на один меньшей высоты и делается ещё операций. Тогда итоговая трудоёмкость этой операции равна , где — высота дерева.
merge
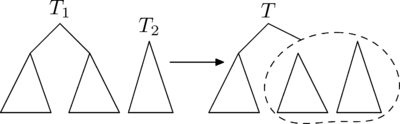
Рассмотрим вторую операцию с декартовыми деревьями — (слить).
С помощью этой операции можно слить два декартовых дерева в одно. Причём, все ключи в первом(левом) дереве должны быть меньше, чем ключи во втором(правом). В результате получается дерево, в котором есть все ключи из первого и второго деревьев:
Рассмотрим принцип работы этой операции. Пусть нужно слить деревья и . Тогда, очевидно, у результирующего дерева есть корень. Корнем станет вершина из или с наибольшим приоритетом . Но вершина с самым большим из всех вершин деревьев и может быть только либо корнем , либо корнем . Рассмотрим случай, в котором корень имеет больший , чем корень . Случай, в котором корень имеет больший , чем корень , симметричен этому.
Если корня больше корня , то он и будет являться корнем. Тогда левое поддерево совпадёт с левым поддеревом . Справа же нужно подвесить объединение правого поддерева и дерева .
Псевдокод
Treap merge(t1: Treap, t2: Treap): if t2 == return t1 if t1 == return t2 else if t1.y > t2.y t1.right = merge(t1.right, t2) return t1 else t2.left = merge(t1, t2.left) return t2
Время работы
Рассуждая аналогично операции , приходим к выводу, что трудоёмкость операции равна , где — высота дерева.
insert
Операция добавляет в дерево элемент , где — ключ, а — приоритет.
Представим что элемент , это декартово дерево из одного элемента, и для того чтобы его добавить в наше декартово дерево , очевидно, нам нужно их слить. Но может содержать ключи как меньше, так и больше ключа , поэтому сначала нужно разрезать по ключу .
- Реализация №1
- Разобьём наше дерево по ключу, который мы хотим добавить, то есть .
- Сливаем первое дерево с новым элементом, то есть .
- Сливаем получившиеся дерево со вторым, то есть .
- Реализация №2
- Сначала спускаемся по дереву (как в обычном бинарном дереве поиска по ), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше .
- Теперь вызываем от найденного элемента (от элемента вместе со всем его поддеревом)
- Полученные и записываем в качестве левого и правого сына добавляемого элемента.
- Полученное дерево ставим на место элемента, найденного в первом пункте.
В первой реализации два раза используется , а во второй реализации слияние вообще не используется.
remove
Операция удаляет из дерева элемент с ключом .
- Реализация №1
- Разобьём наше дерево по ключу, который мы хотим удалить, то есть .
- Теперь отделяем от первого дерева элемент , то есть самого левого ребёнка дерева .
- Сливаем первое дерево со вторым, то есть .
- Реализация №2
- Спускаемся по дереву (как в обычном бинарном дереве поиска по ), и ищем удаляемый элемент.
- Найдя элемент, вызываем его левого и правого сыновей
- Результат процедуры ставим на место удаляемого элемента.
В первой реализации один раз используется , а во второй реализации разрезание вообще не используется.
Построение декартова дерева
Пусть нам известно из каких пар требуется построить декартово дерево, причём также известно, что .
Алгоритм за
Отсортируем все приоритеты по убыванию за и выберем первый из них, пусть это будет . Сделаем корнем дерева. Проделав то же самое с остальными вершинами получим левого и правого сына . В среднем высота Декартова дерева (см. далее) и на каждом уровне мы сделали операций. Значит такой алгоритм работает за .
Другой алгоритм за
Отсортируем пары по убыванию и положим их в очередь. Сперва достанем из очереди первые элемента и сольём их в дерево и положим в конец очереди, затем сделаем то же самое со следующими двумя и т.д. Таким образом, мы сольём сначала деревьев размера , затем деревьев размера и так далее. При этом на уменьшение размера очереди в два раза мы будем тратить суммарно время на слияния, а всего таких уменьшений будет . Значит полное время работы алгоритма будет .
Алгоритм за
Будем строить дерево слева направо, то есть начиная с по , при этом помнить последний добавленный элемент . Он будет самым правым, так как у него будет максимальный ключ, а по ключам декартово дерево представляет собой двоичное дерево поиска. При добавлении , пытаемся сделать его правым сыном , это следует сделать если , иначе делаем шаг к предку последнего элемента и смотрим его значение . Поднимаемся до тех пор, пока приоритет в рассматриваемом элементе меньше приоритета в добавляемом, после чего делаем его правым сыном, а предыдущего правого сына делаем левым сыном .
Заметим, что каждую вершину мы посетим максимум дважды: при непосредственном добавлении и, поднимаясь вверх (ведь после этого вершина будет лежать в чьём-то левом поддереве, а мы поднимаемся только по правому). Из этого следует, что построение происходит за .
Случайные приоритеты
Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей , будет равна . Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно.
Высота в декартовом дереве с случайными приоритетами
| Теорема: | ||||||
В декартовом дереве из узлов, приоритеты которого являются случайными величинами c равномерным распределением, средняя глубина вершины . | ||||||
| Доказательство: | ||||||
|
Будем считать, что все выбранные приоритеты попарно различны. Для начала введём несколько обозначений:
В силу обозначений глубину вершины можно записать как количество предков:
Теперь можно выразить математическое ожидание глубины конкретной вершины:
Для подсчёта средней глубины вершин нам нужно сосчитать вероятность того, что вершина является предком вершины , то есть . Введём новое обозначение:
Так как распределение приоритетов равномерное, каждая вершина среди может иметь максимальный приоритет, мы немедленно приходим к следующему равенству: Подставив последнее в нашу формулу с математическим ожиданием получим: (здесь мы использовали неравенство )
| ||||||
Таким образом, среднее время работы операций и будет .