Проблема четырёх красок

Теорема (Проблема четырех красок):

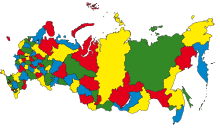
Теорема о четырёх красках — утверждение о том, что всякую карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. Под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются.

Карта России раскрашенная в [math]4[/math] цвета

Общие идеи доказательства

Начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится планарный граф. Тогда следующая теорема эквивалентна теореме выше:

Теорема (Хроматическое число планарного графа):

Хроматическое число планарного графа не превосходит [math]4[/math].

4-раскраска планарного графа

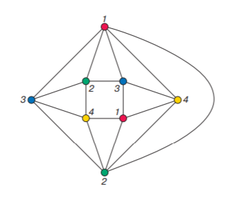
Теперь, если есть грань, образованная нашим планарным графом, не являющаяся треугольником, мы можем добавлять ребра без внедрения новых вершин до тех пор, пока все грани не станут треугольниками. Если полученный граф является раскрашиваемым в не более чем [math]4[/math] цвета, то и исходный граф раскрашиваем так же (так как удаление ребер не увеличивает хроматическое число). Поэтому достаточно доказать теорему для триангулированных графов, и без потери общности мы предполагаем, что граф триангулирован.

Для дальнейших рассуждений нам понадобится следующее утверждение:

Утверждение:

Для триангулированного графа [math]\sum\limits^{D}_{i=1}(6-i)v_{i} = 12[/math], где [math]v_{i}[/math] — количество вершин степени [math]i[/math], а [math]D[/math] — максимальная степень вершины в графе.

[math]\triangleright[/math]

Так как граф триангулирован, то [math]2E=3F[/math], где [math]E[/math] — количество ребер, а [math]F[/math] — количество граней. Из формулы Эйлера [math]V - E + \dfrac{2}{3}E = 2 ~\rightarrow~ 6V - 2E = 6\sum\limits_{i=1}^{D}v_{i} - \sum\limits_{i=1}^{D}iv_{i} = \sum\limits_{i=1}^{D}(6 - i)v_{i} = 12[/math]

[math]\triangleleft[/math]

Из данного утверждения следует, что в графе существует вершина степени не больше [math]5[/math].

Докажем теорему от противного. Пусть у нас существует граф, который требует хотя бы [math]5[/math] цветов для раскраски. Среди всех таких графов существует минимальный, то есть такой граф [math]G[/math], что удаление любой вершины из него делает его [math]4[/math]-раскрашиваемым.

Утверждение:

В [math]G~\nexists [/math] [math]v \in V[/math] : [math]deg(v) \leqslant 4[/math]

[math]\triangleright[/math]

Если в [math]G[/math] есть вершина степени [math]3[/math], то мы можем просто удалить ее из графа, раскрасить полученный граф в [math]4[/math] цвета, вернуть удаленную вершину и покрасить ее в один из цветов, не занятых соседями. Аналогично теореме Хивуда доказывается, что удалив вершину степени [math]4[/math] также всегда можно раскрасить граф в [math]4[/math] цвета.

[math]\triangleleft[/math]

Для вершины степени [math]5[/math] аналогичное утверждение неверно, поэтому нельзя просто удалить ее. Тогда вместо [math]1[/math] вершины будем рассматривать произвольный связный подграф из нескольких вершин (назовем его конфигурацией). Сводимыми назовем такие конфигурации, что если при их удалении граф [math]4[/math]-раскрашиваемый, то его окраска может быть изменена таким образом, что при возвращении конфигурации граф также можно раскрасить в [math]4[/math] цвета. Например, конфигурация состоящая из [math]1[/math] вершины степени не больше [math]4[/math] является сводимой (было доказано выше). Неизбежной конфигурацией назовем такое множество конфигураций, что хотя бы одна из конфигураций этого множества обязана быть в нашем графе.

Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф [math]G[/math] все равно [math]4[/math]-раскрашиваем, доказательство будет завершено. Основным методом для нахождения такой конфигурации является метод разгрузки.

Приведем пример нахождения неизбежной конфигурации:

Утверждение:

В планарном графе есть вершина степени не больше [math]4[/math] или конфигурация, состоящая из [math]2[/math] вершин степени [math]5[/math] или из вершины степени [math]5[/math] и степени [math]6[/math]

[math]\triangleright[/math]

Зададим функцию [math]f(v) = 6-deg(v)[/math] и назовем [math]f(v)[/math] грузом вершины [math]v[/math]. Предположим что наше утверждение неверно. Следовательно, в графе нет вершин степени не больше [math]4[/math]. Тогда положительный груз есть только у вершин степени [math]5[/math] (и он равен единице). У вершин степени [math]6[/math] груз нулевой, а у всех остальных вершин — отрицательный. По первому доказанному выше утверждению мы знаем, что [math]\sum\limits_{v \in V}f(v) = 12 \gt 0[/math]. Значит вершины степени [math]5[/math] должны компенсировать все отрицательные грузы других вершин. Пусть каждая такая вершина отдает по [math]\dfrac{1}{5}[/math] своего груза соседям. Тогда у всех вершин степени [math]5[/math] и [math]6[/math] груз останется равен [math]0[/math], так как вершины степени [math]5[/math] не смежны с вершинами степени [math]5[/math] и [math]6[/math] по предположению. Рассмотрим все остальные вершины. Поскольку мы проводим доказательство для триангулированных графов, то соседи вершины [math]v[/math] образуют цикл и на этом цикле [math]2[/math] вершины степени [math]5[/math] не могут быть рядом. Значит у вершины степени [math]i[/math] не может быть больше чем [math]\bigg\lfloor\dfrac{i}{2}\bigg\rfloor[/math] соседей степени [math]5[/math]. Однако [math](6 - i) + \dfrac{1}{5}\bigg\lfloor\dfrac{i}{2}\bigg\rfloor \lt 0[/math] для [math]i \geqslant 7[/math], следовательно, сумма грузов отрицательна. Получено противоречие.

[math]\triangleleft[/math]

Выше мы получили неизбежную конфигурацию, состоящую из небольшого количество элементов. Подобными действиями К. Аппель и В. Хакен провели [math]487[/math] операций разгрузки и получили неизбежную конфигурацию из [math]1482[/math] конфигураций. Для доказательства раскрашиваемости графов с ними был использован компьютер. Из-за сложности этого доказательства, мы не можем рассмотреть его целиком, поэтому более подробно ознакомиться со всеми операциями разгрузки и изучить полученные компьютером раскраски конфигураций можно в двух оригинальных статьях Аппеля и Хакена .

См. также

• Раскраска графа
• Хроматическое число планарного графа

Источники информации

• Лекция Thomas Fernique
• Four color theorem
• Discharging method