Формула включения-исключения — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показана 61 промежуточная версия 17 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Формула | + | |
| + | == Формула включения-исключения == | ||
| + | {{Определение | ||
| + | |definition='''Формула включения-исключения''' (англ. ''Inclusion-exclusion principle'') {{---}} комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений. | ||
| + | }} | ||
[[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | [[Файл:пересечение двух множеств.svg.png|thumb|right|Случай для двух множеств]] | ||
| − | + | Для случая из двух множеств <tex dpi = "140"> A, B </tex> формула включения-исключения имеет следующий вид: | |
<center> | <center> | ||
| − | <tex> | A \cup B | = | A | + | B | - | A \cap B |</tex> | + | <tex dpi = "140"> | A \cup B | = | A | + | B | - | A \cap B |</tex> |
</center> | </center> | ||
| − | В сумме <tex> | + | В силу того, что в сумме <tex dpi = "140"> | A | + | B |</tex> элементы пересечения <tex dpi = "140"> A \cap B </tex> учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера{{---}}Венна для двух множеств, приведенной на рисунке справа. |
| + | |||
| + | Для случая с большим количеством рассматриваемых множеств <tex dpi = "140"> n </tex> процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы. | ||
| − | + | Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств. | |
{{Теорема | {{Теорема | ||
| − | |statement=Пусть <tex> A = \bigcup \limits_{i=1}^{n}A_i </tex> , тогда по формуле | + | |statement=Пусть <tex dpi = "140"> A = \bigcup \limits_{i=1}^{n}A_i </tex> , тогда по формуле включения-исключения: <center> <tex dpi = "140"> | A | = \sum \limits_{I \in 2^N -1} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> </center> |
| − | Причем <tex> N = \{ 1,2, \ldots ,n \} </tex>. Здесь за <tex> 2^N </tex> обозначим множество всех непустых подмножеств <tex> N </tex>. | + | Причем <tex dpi = "140"> N = \{ 1,2, \ldots ,n \} </tex>. Здесь за <tex dpi = "140"> 2^N - 1 </tex> обозначим множество всех непустых подмножеств <tex dpi = "140"> N </tex>. |
||proof= | ||proof= | ||
| − | Приведем два разноплановых доказательства | + | Приведем два разноплановых доказательства теоремы. |
| − | '''I. Комбинаторное доказательство | + | '''I. Комбинаторное доказательство теоремы.''' |
| − | Рассмотрим некоторый элемент <tex> x \in \bigcup \limits_{i=1}^{n}A_i </tex>. Пусть <tex> x \in \bigcap \limits_{j=1}^{t}A_{i_j} </tex>. Тогда найдем число вхождений элемента <tex> x </tex> в правую часть формулы. | + | Рассмотрим некоторый элемент <tex dpi = "140"> x \in \bigcup \limits_{i=1}^{n}A_i </tex>. Пусть <tex dpi = "140"> x \in \bigcap \limits_{j=1}^{t}A_{i_j} </tex>. Тогда найдем число вхождений элемента <tex dpi = "140"> x </tex> в правую часть формулы. |
| − | <tex>k = (-1) ^ {t + 1} {t \choose t} + (-1) ^ {t} {t \choose {t - 1}} + \ldots + (-1)^2 {t \choose 1 | + | <tex dpi = "140">k = (-1) ^ {t + 1} {t \choose t} + (-1) ^ {t} {t \choose {t - 1}} + \ldots + (-1)^2 {t \choose 1} = -\sum \limits_{j = 1}^{t} (-1)^j {t \choose j} </tex><tex dpi = "140"> = {t \choose 0} - \sum \limits_{j = 0 |
| + | }^{t} (-1)^j {t \choose j} </tex> | ||
| + | Докажем, что <tex dpi = "140"> \sum \limits_{j = 0}^{t} (-1)^j {t \choose j} = 0</tex> | ||
| − | + | В силу того, что <tex dpi = "140"> (1 + (-1)) ^ t = {t \choose 0} 1^t (-1)^0 + {t \choose 1} 1 ^ {t - 1} (-1) ^ 1 + \ldots + {t \choose t} 1^0 (-1)^t = \sum \limits_{j = 0}^{t} (-1)^j {t \choose j}</tex>, имеем <tex dpi = "140"> 0 = (1 + (-1)) ^ t = \sum \limits_{j = 0}^{t} (-1)^j {t \choose j}</tex>, то равенство доказано. | |
| − | + | Таким образом, <tex dpi = "140"> k = {t \choose 0} - \sum \limits_{j = 0}^{t} (-1)^j = 1 - 0 = 1</tex>, то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. | |
| − | + | '''II. Доказательство теоремы по индукции.''' | |
| + | Пусть <tex dpi = "130">~l</tex> {{---}} это количество множеств, мощность пересечения которых мы ищем. Для случая <tex dpi = "130">~l=1</tex> равенство обращается в тривиальное (<tex dpi = "130"> |A| = |A_1| </tex> {{---}} истинно). Для случая <tex dpi = "130"x>~l=2</tex> справедливость теоремы пояснена выше. Таким образом, <tex dpi = "130">~l=2</tex> {{---}} база индукции. | ||
| − | Пусть <tex> A </tex> {{---}} объединение <tex>~n</tex> множеств. Очевидно, что <tex> A = \bigcup \limits_{i=1}^{n}A_i = \left( {\bigcup \limits_{i=1}^{n-1}A_i} \right) \cup A_n </tex>. Пусть <tex> B = \bigcup \limits_{i=1}^{n-1}A_i </tex>; <tex>N' = \{ 1,2, \ldots ,n-1 \} </tex>. | + | Предположим, что для <tex dpi = "130">~l=n-1</tex> равенство верно. Докажем, что равенство истинно для <tex dpi = "130">~l=n</tex> |
| + | |||
| + | |||
| + | Пусть <tex dpi = "130"> A </tex> {{---}} объединение <tex dpi = "130">~n</tex> множеств. Очевидно, что <tex dpi = "130"> A = \bigcup \limits_{i=1}^{n}A_i = \left( {\bigcup \limits_{i=1}^{n-1}A_i} \right) \cup A_n </tex>. Пусть <tex dpi = "130"> B = \bigcup \limits_{i=1}^{n-1}A_i </tex>; <tex dpi = "130">N' = \{ 1,2, \ldots ,n-1 \} </tex>. | ||
Исходя из предположения индукции, имеем, что | Исходя из предположения индукции, имеем, что | ||
| − | <tex> | B | = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> | + | <tex dpi = "130"> | B | = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| </tex> |
| + | |||
| + | |||
| + | Кроме того, так как формула верна для <tex dpi = "130">~l=2</tex> (из базы индукции), то верно равенство <tex dpi = "130"> | A | = | B | + | A_n | - | B \cap A_n | (*)</tex>. | ||
| − | + | Найдем <tex dpi = "130">~| B \cap A_n |</tex>: | |
| − | Очевидно, что <tex> B \cap A_n = \left( \bigcup \limits_{i=1}^{n-1}A_i \right) \cap A_n = \bigcup \limits_{i=1}^{n-1} \left( A_i \cap A_n \right) (**)</tex> | + | Очевидно, что <tex dpi = "130"> B \cap A_n = \left( \bigcup \limits_{i=1}^{n-1}A_i \right) \cap A_n = \bigcup \limits_{i=1}^{n-1} \left( A_i \cap A_n \right) (**)</tex> |
| − | Опираясь на предположение индукции и равенство <tex> (**) </tex> имеем, что <tex> |B \cap A_n| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} \left( A_j \cap A_n \right) \right| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| </tex> | + | Опираясь на предположение индукции и равенство <tex dpi = "130"> (**) </tex> имеем, что <tex dpi = "130"> |B \cap A_n| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} \left( A_j \cap A_n \right) \right| = \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| </tex> |
| − | Подставим полученные значения в <tex>(*)</tex>: | + | Подставим полученные значения в <tex dpi = "130">(*)</tex>: |
| − | <tex> | A | = | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| \right) - \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right)</tex> <tex> =| A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) | + | <tex dpi = "130"> | A | = | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I} A_j \right| \right) - \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right)</tex> <tex dpi = "130"> =| A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) |
</tex> | </tex> | ||
| − | Докажем, что <tex> | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) | + | Докажем, что <tex dpi = "130"> | A_n |+\left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| \right) + \left( \sum \limits_{I \in 2^{N'}} (-1)^{|I|+2} \left| \bigcap \limits_{ j\in I \cup \{ n \} } A_j \right| \right) |
| − | </tex> <tex> = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| </tex> | + | </tex> <tex dpi = "130"> = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| </tex> |
| + | |||
| + | Равенство справедливо, потому что все наборы <tex dpi = "130"> I \in 2^N </tex> можно разбить на две группы : | ||
| + | |||
| + | # <tex dpi = "130"> I \in 2^{N'} </tex> Это означает, что в наборе точно '''не''' будет присутствовать индекс <tex dpi = "130"> n </tex>, а будут все различные варианты индексов остальных множеств, т.е. <tex dpi = "130"> I \in 2^{N'}</tex>. | ||
| + | # <tex dpi = "130">\{n\} \cup I</tex>, где <tex dpi = "130">I \in N'</tex> Аналогично предыдущему, только в наборе будет индекс <tex dpi = "130"> n </tex>. | ||
| + | |||
| + | Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и <tex dpi = "130">|A| = \sum \limits_{I \in 2^N} (-1)^{|I|+1} \left| \bigcap \limits_{ j \in I } A_j \right| </tex> . | ||
| + | Таким образом, для <tex dpi = "130">~l=n</tex> мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. | ||
| + | }} | ||
| + | |||
| + | == Беспорядки == | ||
| + | {{Определение | ||
| + | |id=идентификатор (необязательно), пример: def1. | ||
| + | |definition='''Беспорядок''' (англ. ''Derangement'') — это перестановка чисел от <tex>1</tex> до <tex>n</tex>, в которой ни один элемент не стоит на своём месте. | ||
| + | }} | ||
| + | |||
| + | === Явная формула с использованием принципа включения-исключения === | ||
| + | {{Теорема | ||
| + | |id=идентификатор (необязательно), пример: th1. | ||
| + | |statement= Количество беспорядков порядка <tex>n</tex> равно субфакториалу <ref>[http://ru.wikipedia.org/wiki/%D0%A1%D1%83%D0%B1%D1%84%D0%B0%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D0%B0%D0%BB Википедия {{---}} Субфакториал]</ref> числа <tex>n</tex> (обозначение: <tex>!n</tex>) и вычисляется по формуле: | ||
| + | |||
| + | <tex dpi = "150"> !n = n! - \frac{n!}{1!} + \frac{n!}{2!} - \frac{n!}{3!} + ... + \frac{n!}{n!}(-1)^{n}= \sum_{k=0}^n\frac{n!}{k!}(-1)^{k} </tex> | ||
| + | |proof= | ||
| + | Воспользуемся принципом включения-исключения: обозначим за <tex dpi = "130">A_i</tex> — количество перестановок из <tex dpi = "130">n</tex> элементов, в каждой из которых <tex dpi = "130">i</tex>-ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: | ||
| + | |||
| + | <tex dpi = "140"> \Big |\bigcap_{i=_1}^n \overline{A}_i \Big| = |U|-\sum \limits_{i} |A_i|+\sum \limits_{i < j} |A_i\bigcap A_j|-\sum \limits_{i < j < k} |A_i\bigcap A_j\bigcap A_k|</tex> <tex dpi = "130">+ ... +(-1)^{n}| A_1 \bigcap A_2 \bigcap ... \bigcap A_n | </tex>, где универсум <tex dpi = "130">U</tex> — множество из всех перестановок порядка <tex dpi = "130">n</tex>. | ||
| + | |||
| + | <tex>\overline{A}_i</tex> — количество перестановок, в каждой из которых <tex>i</tex>-ый элемент стоит не на своём <tex>i</tex>-ом месте. | ||
| + | |||
| + | Таким образом <tex dpi = "130">| \bigcap_{i=_1}^n \overline {A}_i |</tex> — количество всех перестановок, в каждой из которых <tex>i</tex>-ый элемент <tex dpi = "130">\neq</tex> <tex dpi = "130">i</tex>,то есть количество искомых беспорядков. | ||
| − | + | <tex dpi = "130">|A_i| = (n - 1)!</tex>, так как <tex dpi = "130">i</tex>-ая позиция занята числом <tex dpi = "130">i</tex>. <tex dpi = "130">\binom{n}{1}</tex> — количество способов выбрать одну <tex dpi = "130">i</tex>-ую позицию <tex dpi = "130"> \Rightarrow \sum \limits_{i = 1}^{n} |A_i| = \binom{n}{1} (n-1)!</tex> | |
| − | + | Рассмотрим <tex dpi = "130"> |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| </tex>, где <tex dpi = "130"> 1\leqslant i_1 < i_2 < ... < i_k \leqslant n </tex>. Так как некоторые <tex dpi = "130">k</tex> позиций <tex dpi = "130">i_1, i_2, ... , i_k </tex> заняты соответствующими числами, то количество способов расставить остальные <tex dpi = "130">n-k</tex> чисел равно <tex dpi = "130">(n-k)!</tex>. То есть <tex dpi = "130"> |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| = (n - k)! </tex> Количество всех способов выбрать <tex dpi = "130">k</tex> позиций <tex dpi = "130">i_1, i_2, ... , i_k </tex> равно <tex dpi = "130">\binom{n}{k} </tex>. Таким образом получаем, что: | |
| − | |||
| − | + | <tex dpi = "130">\sum \limits_{1\leqslant i_1 < i_2 < ... < i_k \leqslant n}^{} |A_{i_1} \bigcap A_{i_2} \bigcap ... \bigcap A_{i_k}| = \binom{n}{k} \cdot(n-k)! </tex> | |
| − | + | ||
| + | Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем: | ||
| + | |||
| + | <tex dpi = "130">| \bigcap_{i=_1}^n \overline{A}_i | = n! + \sum \limits_{k = 1}^{n} (-1)^{k}\binom{n}{k} \cdot (n - k)!.</tex> | ||
| + | |||
| + | Раскрывая <tex dpi = "140">\binom{n}{k}</tex> по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка <tex dpi = "130">n</tex>. | ||
}} | }} | ||
| + | |||
| + | === Рекурретное соотношение для нахождения количества беспорядков === | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement = | ||
| + | Количество беспорядков удовлетворяет рекурсивным соотношениям: | ||
| + | |||
| + | <tex dpi = "140"> d(n)=(n-1)[d(n-1)+d(n-2)] </tex> | ||
| + | |||
| + | и | ||
| + | |||
| + | <tex dpi = "140"> d(n)=n \times d(n-1)+(-1)^{n} </tex>, | ||
| + | |||
| + | где <tex dpi = "140"> d(1)=0 </tex>, а <tex dpi = "140"> d(2)=1 </tex> | ||
| + | |proof = | ||
| + | 1) Докажем второе соотношение: | ||
| + | |||
| + | Так как <tex dpi = "140"> d(n)=!n </tex>, то можно переписать эту формулу, как <tex dpi = "140"> !n=n!(n-1)+(-1)^{n} </tex> | ||
| + | |||
| + | По формуле субфакториала <tex dpi = "140"> !n=n!(\sum \limits_{k = 0}^{n-1} \frac {(-1)^{k}}{k!} + \frac {(-1)^{n}}{n!})=n!\sum \limits_{k = 0}^{n-1} \frac {(-1)^{k}}{k!}+(-1)^{n}=n \times !(n-1)+(-1)^{n}</tex> | ||
| + | |||
| + | 2) Докажем первое соотношение: | ||
| + | |||
| + | У нас есть <tex> n </tex> чисел и столько же мест. Мы должны найти количество способов разместить эти числа так, что ни одно из чисел не оказалось на месте с таким же номером. | ||
| + | |||
| + | Предположим, что первое число оказалось на месте с номером <tex> i </tex>. Это можно сделать <tex> n-1 </tex> способами, так как первое число может оказаться на любом месте, кроме первого. Теперь есть 2 варианта, зависящие от того, окажется ли число с номером <tex> i </tex> на первом месте или нет. | ||
| + | |||
| + | * Число <tex> i </tex> на первом месте. Остается <tex> n-2 </tex> мест и <tex> n-2 </tex> чисел. То есть количество беспорядков от <tex> n-2 </tex> | ||
| + | * Число <tex> i </tex> не может оказаться на первом месте. Это эквивалентно решению задачи с <tex> n-1 </tex> местами и <tex> n-1 </tex> числами (первое число уже заняло место, а остальные еще нет): у каждого числа будет одно запрещенное место (у числа с номером <tex> i </tex> запрещенным будет первое место). Получается количество беспорядков от <tex> n-1 </tex>. | ||
| + | |||
| + | Эти 2 случая не пересекаются и поэтому суммируются. В первом случае число <tex> i </tex> занимает первое место, затем идет распределение остальных чисел, не зависящее от первого и <tex> i </tex>-го чисел. Во втором же случае число с номером <tex> i </tex> попасть на первое место не может, а значит займет какое-то другое место, и распределение остальных чисел уже будет другое. | ||
| + | |||
| + | В итоге получается необходимая формула. | ||
| + | }} | ||
| + | |||
| + | == Задача о перестановках == | ||
| + | |||
| + | Сколько есть перестановок чисел от <tex> 0 </tex> до <tex> 9 </tex> таких, что первый элемент больше <tex> 1 </tex>, а последний меньше <tex> 8 </tex>? | ||
| + | |||
| + | Посчитаем количество "плохих" перестановок, то есть таких, у которых первый элемент <tex> \leqslant 1 </tex> (множество таких перестановок обозначим <tex> X </tex>) и/или последний <tex> \leqslant 8 </tex> (множество таких перестановок обозначим <tex> Y </tex>). | ||
| + | |||
| + | Тогда количество "плохих" перестановок по формуле включений-исключений равно: | ||
| + | |||
| + | <tex> |X|+|Y|-|X \cap Y| </tex> | ||
| + | |||
| + | Проведя несложные комбинаторные вычисления, получим: | ||
| + | |||
| + | <tex> 2 \times 9!+2 \times 9! - 2 \times 2 \times 8! </tex> | ||
| + | |||
| + | Отнимая это число от общего числа перестановок <tex> 10! </tex>, получим ответ. | ||
| + | |||
| + | == Задача о нахождении числа взаимно простых четвёрок == | ||
| + | |||
| + | Дано <tex> n </tex> чисел: <tex> a_1, a_2,..., a_n </tex>. Необходимо посчитать количество способов выбрать из них четыре числа так, что они будут взаимно простыми, то есть их НОД равен единице. | ||
| + | |||
| + | Посчитаем число "плохих" четвёрок, то есть таких, в которых все числа делятся на число <tex> d > 1 </tex>. | ||
| + | |||
| + | Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на <tex> d </tex> (но, возможно, делящихся и на больший делитель). | ||
| + | |||
| + | <tex> answer=\sum \limits_{d>1} (-1)^{deg(d)-1} \times f(d) </tex>, | ||
| + | |||
| + | где <tex> deg(d) </tex> — это количество простых в факторизации числа <tex> d </tex>, <tex> f(d) </tex> — количество четвёрок, делящихся на <tex> d </tex>. | ||
| + | |||
| + | Чтобы посчитать функцию <tex> f(d) </tex>, надо просто посчитать количество чисел, кратных <tex> d </tex>, и с помощью биномиальных коэффициентов посчитать число способов выбрать из них четвёрку. | ||
| + | |||
| + | Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Производящая функция]] | ||
| + | * [[Лемма Бёрнсайда и Теорема Пойа]] | ||
| + | |||
| + | ==Примечания== | ||
| + | |||
| + | <references /> | ||
| + | == Источники информации == | ||
| + | * [[wikipedia:ru:Беспорядок_(перестановка)|Википедия — Беспорядок]] | ||
| + | * [http://en.wikipedia.org/wiki/Derangement Wikipedia — Derangement] | ||
| + | * Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, Изд. 4-е, исправленное - МЦНМО, 2013 ISBN 978-5-4439-0052-0 | ||
| + | * Р. Стенли, Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108. | ||
| + | |||
| + | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Комбинаторика]] | [[Категория: Комбинаторика]] | ||
Текущая версия на 19:33, 4 сентября 2022
Формула включения-исключения
| Определение: |
| Формула включения-исключения (англ. Inclusion-exclusion principle) — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений. |
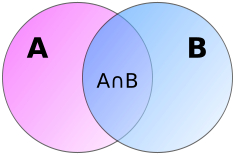
Для случая из двух множеств формула включения-исключения имеет следующий вид:
В силу того, что в сумме элементы пересечения учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.
Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.
Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.
| Теорема: |
Пусть , тогда по формуле включения-исключения: |
| Доказательство: |
|
Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент . Пусть . Тогда найдем число вхождений элемента в правую часть формулы.
Докажем, что В силу того, что , имеем , то равенство доказано. Таким образом, , то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное ( — истинно). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для
Равенство справедливо, потому что все наборы можно разбить на две группы :
Как видно из равенства, первое и третье слагаемое "отвечают" за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана. |
Беспорядки
| Определение: |
| Беспорядок (англ. Derangement) — это перестановка чисел от до , в которой ни один элемент не стоит на своём месте. |
Явная формула с использованием принципа включения-исключения
| Теорема: |
Количество беспорядков порядка равно субфакториалу [1] числа (обозначение: ) и вычисляется по формуле:
|
| Доказательство: |
|
Воспользуемся принципом включения-исключения: обозначим за — количество перестановок из элементов, в каждой из которых -ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: , где универсум — множество из всех перестановок порядка . — количество перестановок, в каждой из которых -ый элемент стоит не на своём -ом месте. Таким образом — количество всех перестановок, в каждой из которых -ый элемент ,то есть количество искомых беспорядков. , так как -ая позиция занята числом . — количество способов выбрать одну -ую позицию Рассмотрим , где . Так как некоторые позиций заняты соответствующими числами, то количество способов расставить остальные чисел равно . То есть Количество всех способов выбрать позиций равно . Таким образом получаем, что:
Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем: Раскрывая по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка . |
Рекурретное соотношение для нахождения количества беспорядков
| Утверждение: |
Количество беспорядков удовлетворяет рекурсивным соотношениям:
и , где , а |
|
1) Докажем второе соотношение: Так как , то можно переписать эту формулу, как По формуле субфакториала 2) Докажем первое соотношение: У нас есть чисел и столько же мест. Мы должны найти количество способов разместить эти числа так, что ни одно из чисел не оказалось на месте с таким же номером. Предположим, что первое число оказалось на месте с номером . Это можно сделать способами, так как первое число может оказаться на любом месте, кроме первого. Теперь есть 2 варианта, зависящие от того, окажется ли число с номером на первом месте или нет.
Эти 2 случая не пересекаются и поэтому суммируются. В первом случае число занимает первое место, затем идет распределение остальных чисел, не зависящее от первого и -го чисел. Во втором же случае число с номером попасть на первое место не может, а значит займет какое-то другое место, и распределение остальных чисел уже будет другое. В итоге получается необходимая формула. |
Задача о перестановках
Сколько есть перестановок чисел от до таких, что первый элемент больше , а последний меньше ?
Посчитаем количество "плохих" перестановок, то есть таких, у которых первый элемент (множество таких перестановок обозначим ) и/или последний (множество таких перестановок обозначим ).
Тогда количество "плохих" перестановок по формуле включений-исключений равно:
Проведя несложные комбинаторные вычисления, получим:
Отнимая это число от общего числа перестановок , получим ответ.
Задача о нахождении числа взаимно простых четвёрок
Дано чисел: . Необходимо посчитать количество способов выбрать из них четыре числа так, что они будут взаимно простыми, то есть их НОД равен единице.
Посчитаем число "плохих" четвёрок, то есть таких, в которых все числа делятся на число .
Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на (но, возможно, делящихся и на больший делитель).
,
где — это количество простых в факторизации числа , — количество четвёрок, делящихся на .
Чтобы посчитать функцию , надо просто посчитать количество чисел, кратных , и с помощью биномиальных коэффициентов посчитать число способов выбрать из них четвёрку.
Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.
См. также
Примечания
Источники информации
- Википедия — Беспорядок
- Wikipedia — Derangement
- Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, Изд. 4-е, исправленное - МЦНМО, 2013 ISBN 978-5-4439-0052-0
- Р. Стенли, Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108.