Симуляция одним распределением другого — различия между версиями
Borisov (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 46 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | ||
==Распределение== | ==Распределение== | ||
| − | [[Файл: | + | {{Определение |
| − | + | |definition = | |
| + | Пусть <tex>\xi</tex> является случайной величиной, а <tex>A</tex> {{---}} ее множеством значений. Функция <tex>P: 2^A \rightarrow \mathbb R,</tex> определенная как <tex>P(B) = P(\xi \in B),</tex> называется '''распределением случайной величины''' (англ. ''probability distribution''), то есть представляет собой набор вероятностей, с которыми случайная величина принимает те или иные значения. }} | ||
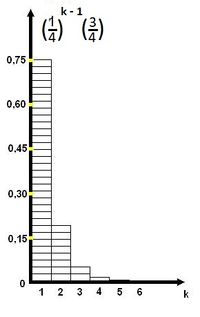
| + | [[Файл:РаспределениеUPD.jpeg|200px|thumb|right|Геометрическое распределение с <tex>p = \dfrac {3} {4}</tex>]] | ||
| + | |||
| + | Закон распределения дискретной случайной величины <tex>\xi</tex> задается таблицей: | ||
| + | |||
| + | <tex>\xi: \begin{pmatrix} | ||
| + | x_1 & x_2 & \ldots & x_n \\ | ||
| + | p_1 & p_2 & \ldots & p_n\end{pmatrix}, </tex> | ||
| + | |||
| + | где <tex>x_1 < x_2 < \ldots < x_n</tex> {{---}} всевозможные значения величины <tex>\xi,</tex> а <tex>p_i(i = 1, \ldots, | ||
| + | n)</tex> {{---}} их вероятности, то есть <tex>p_i = P(\xi = x_i).</tex> | ||
| + | |||
| + | При этом должно выполняться равенство: <tex>p_1 + p_2 + \ldots + p_n = 1.</tex> | ||
| + | |||
| + | Это равенство означает, что при испытании одно из значений заведомо реализуется. Таблица показывает, как суммарная вероятность <tex>100\%</tex> распределяется по возможным значениям случайной величины. | ||
| + | |||
| + | Для непрерывных случайных величин задание закона распределения в виде такой таблицы невозможно, поэтому его задают двумя другими способами: | ||
| + | |||
| + | :#С помощью [[Дискретная_случайная_величина#.D0.A4.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D1.8F_.D1.80.D0.B0.D1.81.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F|функции распределения]] <tex>F (x);</tex> | ||
| + | :#С помощью [[Дискретная_случайная_величина#.D0.A4.D1.83.D0.BD.D0.BA.D1.86.D0.B8.D1.8F_.D0.BF.D0.BB.D0.BE.D1.82.D0.BD.D0.BE.D1.81.D1.82.D0.B8_.D1.80.D0.B0.D1.81.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F_.D0.B2.D0.B5.D1.80.D0.BE.D1.8F.D1.82.D0.BD.D0.BE.D1.81.D1.82.D0.B5.D0.B9|плотности вероятности]] <tex>f (x).</tex> | ||
==Примеры распределений== | ==Примеры распределений== | ||
| − | + | ===Биномиальное распределение (закон Бернулли)=== | |
| − | + | {{Определение | |
| − | + | |definition= | |
| + | Дискретная случайная величина <tex>\xi</tex> называется '''биномиальной''' (англ. ''binomial random variable'') с параметрами <tex>(n, p),</tex> если она принимает значения от <tex>0</tex> до <tex>n</tex> и вероятности вычисляются по формуле <tex>p_i = P(\xi = i) = \dbinom{n}{k} p^k q^{n - k},</tex> где <tex>i = 1, \ldots, n;</tex> <tex>q = 1 - p,</tex> <tex>p \in (0, 1).</tex>}} | ||
| + | |||
| + | ===Нормальное распределение (распределение Гаусса)=== | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Непрерывную случайную величину <tex>\xi</tex> называют '''нормальной''' (англ. ''normal deviate'') с параметрами <tex>(a, \sigma)</tex> и пишут <tex>\xi = N (a, \sigma),</tex> если ее плотность вероятности дается формулой | ||
| + | <tex>f(x) = \dfrac {1} {\sigma \sqrt{2\pi}} {\large e^{-\frac {(x - a)^2} {2\sigma^2}}}.</tex>}} | ||
| + | |||
| + | ===Равномерное распределение=== | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Непрерывная случайная величина <tex>\xi</tex> называется '''равномерно распределенной''' (англ. ''uniformly distributed random variable'') на <tex>[a, b],</tex> если ее плотность вероятности дается формулой | ||
| + | <tex> | ||
| + | f(x)= | ||
| + | \begin{cases} | ||
| + | \dfrac {1} {b - a}, & \mbox{if } x \in [a, b] \\ | ||
| + | 0, & \mbox{otherwise.} | ||
| + | \end{cases}</tex>}} | ||
==Симуляция распределений== | ==Симуляция распределений== | ||
Для того, чтобы создать необходимое распределение вероятностей, достаточно иметь последовательность независимых случайных величин типа "честной монеты". | Для того, чтобы создать необходимое распределение вероятностей, достаточно иметь последовательность независимых случайных величин типа "честной монеты". | ||
| + | |||
Например, для создания схемы с двумя исходами $A_1$ и $A_2$: | Например, для создания схемы с двумя исходами $A_1$ и $A_2$: | ||
| − | + | $P(A_1)=\dfrac{3}{4}$ $,$ $P(A_2)=\dfrac{1}{4}$ | |
| − | можно из датчика случайных двоичных | + | можно из датчика случайных двоичных величин получить два результата "честной монеты" $\delta_1$ и $\delta_2$ и, например, при $\delta_1 = \delta_2 = 1$ выработать исход $A_2$, а в остальных случаях $A_1$. |
| + | |||
Аналогично для схемы с четырьмя исходами | Аналогично для схемы с четырьмя исходами | ||
| − | + | $P(A_1)=\dfrac{3}{16}$ $,$ $P(A_2)=\dfrac{1}{16}$ $,$ $P(A_3)=\dfrac{8}{16}$ $,$ $P(A_4)=\dfrac{4}{16}$ | |
| − | можно получить четыре | + | можно получить четыре результата "честной монеты" $\delta_1$ $,$ $\delta_2$ $,$ $\delta_3$ $,$ $\delta_4$ и любым способом сопоставить трём из 16 возможных наборов исход $A_1$, одному $-$ $A_2$, восьми $-$ $A_3$, четырём $-$ $A_4$. |
| + | |||
Если же вероятности исходов не кратны $2^{-k}$, можно применить два различных варианта действий. | Если же вероятности исходов не кратны $2^{-k}$, можно применить два различных варианта действий. | ||
:#Можно приблизить вероятности двоичными дробями (с любой точностью), далее работать с полученными приближёнными значениями | :#Можно приблизить вероятности двоичными дробями (с любой точностью), далее работать с полученными приближёнными значениями | ||
| − | :#Пусть все вероятности $n_i$ $-$ дроби со знаменателем $r$. Найдём $k$, для которого $r < 2^k$. Предложим схему с $k$ | + | :#Пусть все вероятности $n_i$ $-$ дроби со знаменателем $r$. Найдём $k$, для которого $r < 2^k$. Предложим схему с $k$ результатами "честной монеты", в которой $r$ наборов используются для выработки случайного исхода, а остальные $2^{k}-r$ наборов объявляются "неудачными" и требуют повторного эксперимента (пока не встретится удачный). Чем выше доля полезных исходов равная $r2^{-k}$, тем схема будет эффективнее. |
| − | Количество | + | |
| − | + | Количество результатов "честной монеты" $\lambda$, которые необходимы для формирования случайного исхода, $-$ это случайная величина. Её математическое ожидание: | |
| − | Можно сделать схему более экономной, | + | |
| + | $E\lambda = \dfrac{1}{2}\cdot1+\dfrac{1}{4}\cdot2+\dfrac{1}{8}\cdot3+\dfrac{1}{16}\cdot3+\dfrac{1}{16}\cdot4 = 1\dfrac{7}{8}.$ | ||
| + | |||
| + | Можно сделать схему более экономной, если использовать датчик, равномерно формирующий число из диапазона $[0, 1]$. Образуем по данному набору вероятностей $p_i$ накопленные суммы $s_i$, такие, что $s_0 = 0; s_i = s_{i-1} + p_i,$ для $i > 0$. Случайный исход будет вырабатываться так: по полученному из датчика случайному числу $\gamma$ находится такой индекс $i$, для которого $s_{i-1} < \gamma \leqslant s_i$. Найденное значение индекса $i$ и определяет исход $A_i$. Индекс $i$ можно определять непосредственно просмотром $s_i$ подряд. | ||
| + | |||
| + | Рассмотрим приведенный выше пример с четырьмя исходам. В данном случае суммы $s_0, \ldots, s_4$ будут принимать значения <tex>0,</tex> <tex>\dfrac{3}{16},</tex> <tex>\dfrac{4}{16},</tex> <tex>\dfrac{12}{16}</tex> и <tex>1</tex> соответственно. Значению $\gamma = 0,5$ будет соответствовать $i = 3$, то есть оно будет определять исход события $A_3.$ Таким же образом, $\gamma = 0,985$ определяет исход события $A_4.$ | ||
| + | |||
| + | Если $k$ велико, можно применять специальные приёмы ускоренного поиска, например, деление множества индексов примерно пополам. | ||
| + | |||
| + | ==Общий случай== | ||
| + | {|class = "wikitable" style="text-align:center;" | ||
| + | | рис. <tex>1</tex> || рис. <tex>2</tex> || рис. <tex>3</tex> | ||
| + | |- | ||
| + | |width = "280px"| [[Файл:Sim pic1.JPG|270px]] ||width = "280px"|[[Файл:Sim pic2.JPG|270px]] ||width = "280px"|[[Файл:Sim pic3.JPG|270px]] | ||
| + | |} | ||
| + | |||
| + | Допустим у нас есть распределение <tex>p.</tex> Нам нужно получить распределение <tex>q</tex>. | ||
| + | |||
| + | Для начала рассмотрим случай, когда все <tex>p_i = \dfrac{1}{k},</tex> а в распределении <tex>q </tex> количество элементарных исходов равно <tex>2</tex> <tex>(</tex>рис. <tex>1).</tex> | ||
| − | + | Проводим эксперимент: если попадаем в область пересекающуюся с <tex> q_1 </tex> и <tex> q_2,</tex> то увеличиваем ее и повторяем эксперимент. На рис. <tex>1</tex> красным обозначено распределение <tex> q. </tex> Вероятность того, что на этом шаге эксперимент не закончится {{---}} <tex>\dfrac{1}{k}.</tex> Математическое ожидание количества экспериментов {{---}} <tex> \dfrac{k}{k-1}, | |
| + | max(\dfrac{k}{k-1}) = 2</tex> <tex>(</tex>при <tex>k = 2).</tex> | ||
| − | |||
| − | + | Теперь рассмотрим случай, когда все элементарные исходы <tex>p_i</tex> по-прежнему равновероятны <tex>(p_i = \dfrac{1}{k}),</tex>а количество элементарных исходов распределения <tex>q</tex> равно <tex>n (\sum\limits_{j=1}^{n}q_j = 1)</tex> <tex>(</tex>рис. <tex>2).</tex> Повторим эксперимент <tex> t </tex> раз. | |
| − | |||
| − | |||
| − | |||
| − | + | <tex> k^t \geqslant 2n, t \geqslant \log\limits_{k}2n </tex> | |
| − | + | Отрезок разбился на <tex> k^t </tex> отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов <tex> \approx 2t </tex> | |
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | + | <tex>p_i, \sum\limits_{i}p_i = 1,</tex> <tex>q_j, \sum\limits_{j}q_j = 1</tex> | |
| − | </ | ||
| − | + | Берем <tex>p_i</tex>, и пусть оно максимальной длины <tex>(</tex>рис. <tex>3).</tex> Проводим <tex>t</tex> экспериментов. <tex>{p_i}^t < \dfrac{1}{2n}, </tex> все остальные еще меньше. Суммарная длина отрезков не больше <tex>\dfrac{1}{2}.</tex> Нужно <tex> t \geqslant \log\limits_{p}\dfrac{1}{2n} .</tex> | |
| − | |||
| − | + | Таким образом, из любого исходного распределения мы можем получить нужное нам распределение. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==См. также== | ==См. также== | ||
*[[Условная вероятность]] | *[[Условная вероятность]] | ||
| Строка 76: | Строка 108: | ||
*[[Дисперсия случайной величины]] | *[[Дисперсия случайной величины]] | ||
| − | == | + | ==Источники информации== |
| − | *Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. - М., Физматлит, 1984. | + | *Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. {{---}} М., Физматлит, 1984, {{---}} стр. 71. |
| − | *[http://sheen.me/books/spec/apia.djvu Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн - Алгоритмы. Построение и анализ | + | *[http://sheen.me/books/spec/apia.djvu Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн {{---}} Алгоритмы. Построение и анализ {{---}} М. : ООО "И. Д. Вильямс", 2013. {{---}} 1328 с. {{---}} стр. 1254.] |
| − | *Романовский И.В. | + | *Романовский И. В. {{---}} Элементы теории вероятностей и математической статистики (теория и задачи): учебное пособие. {{---}} Омск, издатель ИП Скорнякова Е.В., 2012. {{---}} 189 с. {{---}} стр. 34. |
| + | |||
| + | |||
| + | [[Категория:Дискретная математика и алгоритмы]] | ||
| + | |||
| + | [[Категория: Теория вероятности ]] | ||
Текущая версия на 19:07, 4 сентября 2022
Содержание
Распределение
| Определение: |
| Пусть является случайной величиной, а — ее множеством значений. Функция определенная как называется распределением случайной величины (англ. probability distribution), то есть представляет собой набор вероятностей, с которыми случайная величина принимает те или иные значения. |
Закон распределения дискретной случайной величины задается таблицей:
где — всевозможные значения величины а — их вероятности, то есть
При этом должно выполняться равенство:
Это равенство означает, что при испытании одно из значений заведомо реализуется. Таблица показывает, как суммарная вероятность распределяется по возможным значениям случайной величины.
Для непрерывных случайных величин задание закона распределения в виде такой таблицы невозможно, поэтому его задают двумя другими способами:
- С помощью функции распределения
- С помощью плотности вероятности
Примеры распределений
Биномиальное распределение (закон Бернулли)
| Определение: |
| Дискретная случайная величина называется биномиальной (англ. binomial random variable) с параметрами если она принимает значения от до и вероятности вычисляются по формуле где |
Нормальное распределение (распределение Гаусса)
| Определение: |
| Непрерывную случайную величину называют нормальной (англ. normal deviate) с параметрами и пишут если ее плотность вероятности дается формулой |
Равномерное распределение
| Определение: |
| Непрерывная случайная величина называется равномерно распределенной (англ. uniformly distributed random variable) на если ее плотность вероятности дается формулой |
Симуляция распределений
Для того, чтобы создать необходимое распределение вероятностей, достаточно иметь последовательность независимых случайных величин типа "честной монеты".
Например, для создания схемы с двумя исходами $A_1$ и $A_2$: $P(A_1)=\dfrac{3}{4}$ $,$ $P(A_2)=\dfrac{1}{4}$ можно из датчика случайных двоичных величин получить два результата "честной монеты" $\delta_1$ и $\delta_2$ и, например, при $\delta_1 = \delta_2 = 1$ выработать исход $A_2$, а в остальных случаях $A_1$.
Аналогично для схемы с четырьмя исходами $P(A_1)=\dfrac{3}{16}$ $,$ $P(A_2)=\dfrac{1}{16}$ $,$ $P(A_3)=\dfrac{8}{16}$ $,$ $P(A_4)=\dfrac{4}{16}$ можно получить четыре результата "честной монеты" $\delta_1$ $,$ $\delta_2$ $,$ $\delta_3$ $,$ $\delta_4$ и любым способом сопоставить трём из 16 возможных наборов исход $A_1$, одному $-$ $A_2$, восьми $-$ $A_3$, четырём $-$ $A_4$.
Если же вероятности исходов не кратны $2^{-k}$, можно применить два различных варианта действий.
- Можно приблизить вероятности двоичными дробями (с любой точностью), далее работать с полученными приближёнными значениями
- Пусть все вероятности $n_i$ $-$ дроби со знаменателем $r$. Найдём $k$, для которого $r < 2^k$. Предложим схему с $k$ результатами "честной монеты", в которой $r$ наборов используются для выработки случайного исхода, а остальные $2^{k}-r$ наборов объявляются "неудачными" и требуют повторного эксперимента (пока не встретится удачный). Чем выше доля полезных исходов равная $r2^{-k}$, тем схема будет эффективнее.
Количество результатов "честной монеты" $\lambda$, которые необходимы для формирования случайного исхода, $-$ это случайная величина. Её математическое ожидание:
$E\lambda = \dfrac{1}{2}\cdot1+\dfrac{1}{4}\cdot2+\dfrac{1}{8}\cdot3+\dfrac{1}{16}\cdot3+\dfrac{1}{16}\cdot4 = 1\dfrac{7}{8}.$
Можно сделать схему более экономной, если использовать датчик, равномерно формирующий число из диапазона $[0, 1]$. Образуем по данному набору вероятностей $p_i$ накопленные суммы $s_i$, такие, что $s_0 = 0; s_i = s_{i-1} + p_i,$ для $i > 0$. Случайный исход будет вырабатываться так: по полученному из датчика случайному числу $\gamma$ находится такой индекс $i$, для которого $s_{i-1} < \gamma \leqslant s_i$. Найденное значение индекса $i$ и определяет исход $A_i$. Индекс $i$ можно определять непосредственно просмотром $s_i$ подряд.
Рассмотрим приведенный выше пример с четырьмя исходам. В данном случае суммы $s_0, \ldots, s_4$ будут принимать значения и соответственно. Значению $\gamma = 0,5$ будет соответствовать $i = 3$, то есть оно будет определять исход события $A_3.$ Таким же образом, $\gamma = 0,985$ определяет исход события $A_4.$
Если $k$ велико, можно применять специальные приёмы ускоренного поиска, например, деление множества индексов примерно пополам.
Общий случай
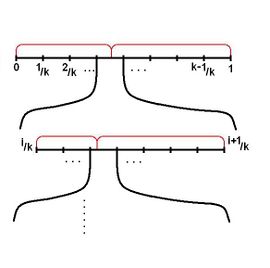
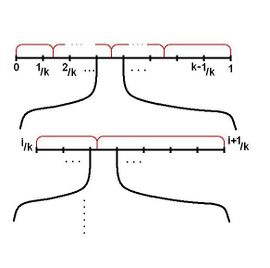
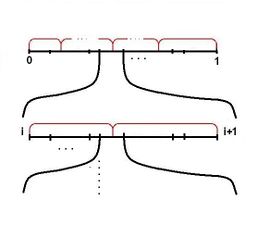
| рис. | рис. | рис. |
 |
 |
|
Допустим у нас есть распределение Нам нужно получить распределение .
Для начала рассмотрим случай, когда все а в распределении количество элементарных исходов равно рис.
Проводим эксперимент: если попадаем в область пересекающуюся с и то увеличиваем ее и повторяем эксперимент. На рис. красным обозначено распределение Вероятность того, что на этом шаге эксперимент не закончится — Математическое ожидание количества экспериментов — при
Теперь рассмотрим случай, когда все элементарные исходы по-прежнему равновероятны а количество элементарных исходов распределения равно рис. Повторим эксперимент раз.
Отрезок разбился на отрезков. Стык будет не более, чем в половине отрезков. Математическое ожидание количества экспериментов
Берем , и пусть оно максимальной длины рис. Проводим экспериментов. все остальные еще меньше. Суммарная длина отрезков не больше Нужно
Таким образом, из любого исходного распределения мы можем получить нужное нам распределение.
См. также
Источники информации
- Боровков А.А. Математическая статистика: оценка параметров, проверка гипотез. — М., Физматлит, 1984, — стр. 71.
- Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн — Алгоритмы. Построение и анализ — М. : ООО "И. Д. Вильямс", 2013. — 1328 с. — стр. 1254.
- Романовский И. В. — Элементы теории вероятностей и математической статистики (теория и задачи): учебное пособие. — Омск, издатель ИП Скорнякова Е.В., 2012. — 189 с. — стр. 34.