Алгоритм Краскала — различия между версиями
(→Реализация) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 123 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | <b>Алгоритм Краскала</b> — алгоритм поиска минимального остовного дерева (minimum spanning tree, MST) во взвешенном неориентированном связном графе. | + | <b>Алгоритм Краскала</b> (англ. ''Kruskal's algorithm'') — алгоритм поиска [[Лемма о безопасном ребре#Необходимые определения | минимального остовного дерева]] (англ. ''minimum spanning tree'', ''MST'') во взвешенном [[Основные определения теории графов#Неориентированные графы | неориентированном связном графе]]. |
==Идея== | ==Идея== | ||
| − | Будем последовательно строить подграф <tex>F</tex> графа <tex>G</tex> ("растущий лес"), | + | Будем последовательно строить подграф <tex>F</tex> графа <tex>G</tex> ("растущий лес"), пытаясь на каждом шаге достроить <tex>F</tex> до некоторого MST. Начнем с того, что включим в <tex>F</tex> все вершины графа <tex>G</tex>. Теперь будем обходить множество <tex>E(G)</tex> в порядке неубывания весов ребер. Если очередное ребро <tex>e</tex> соединяет вершины одной компоненты связности <tex>F</tex>, то добавление его в остов приведет к возникновению цикла в этой компоненте связности. В таком случае, очевидно, <tex>e</tex> не может быть включено в <tex>F</tex>. Иначе <tex>e</tex> соединяет разные компоненты связности <tex>F</tex>, тогда существует <tex> \langle S, T \rangle </tex> [[Лемма о безопасном ребре#Необходимые определения|разрез]] такой, что одна из компонент связности составляет одну его часть, а оставшаяся часть графа — вторую. Тогда <tex>e</tex> — минимальное ребро, пересекающее этот разрез. Значит, из [[Лемма о безопасном ребре#Лемма о безопасном ребре|леммы о безопасном ребре]] следует, что <tex>e</tex> является безопасным, поэтому добавим это ребро в <tex>F</tex>. На последнем шаге ребро соединит две оставшиеся компоненты связности, полученный подграф будет минимальным остовным деревом графа <tex>G</tex>. |
| − | + | Для проверки возможности добавления ребра используется [[СНМ (реализация с помощью леса корневых деревьев) | система непересекающихся множеств]]. | |
==Реализация== | ==Реализация== | ||
| − | < | + | <font color=green>// <tex>G</tex> {{---}} исходный граф</font> |
| − | < | + | <font color=green>// <tex>F</tex> {{---}} минимальный остов</font> |
| − | + | '''function''' <tex>\mathtt{kruskalFindMST}():</tex> | |
| − | + | <tex> \mathtt{F} \leftarrow V(G)</tex> | |
| − | + | <tex>\mathtt{sort}(E(G))\</tex> | |
| − | + | '''for''' <tex>vu \in E(G)</tex> | |
| + | '''if''' <tex>v</tex> и <tex>u</tex> в разных компонентах связности <tex>F</tex> | ||
| + | <tex> \mathtt{F}\ =\ \mathtt{F} \bigcup vu\</tex> | ||
| + | '''return''' <tex> \mathtt{F} </tex> | ||
| + | ==Задача о максимальном ребре минимального веса== | ||
| + | Легко показать, что максимальное ребро в MST минимально. Обратное в общем случае неверно. Но MST из-за сортировки строится за <tex>O(E \log E)</tex>. Однако из-за того, что необходимо минимизировать только максимальное ребро, а не сумму всех рёбер, можно предъявить алгоритм, решающий задачу за линейное время. | ||
| + | С помощью [[Поиск_k-ой_порядковой_статистики_за_линейное_время | алгоритма поиска k-ой порядковой статистики]] найдем ребро-медиану за <tex>O(E)</tex> и разделим множество ребер на два равных по мощности так, чтобы ребра в первом не превосходили по весу ребер во втором. Проверим образуют ли ребра из первого подмножества остов графа, запустив [[Использование_обхода_в_глубину_для_проверки_связности|обход в глубину]]. | ||
| + | * Если да, то рекурсивно запустим алгоритм от него. | ||
| + | * В противном случае сконденсируем получившиеся несвязные компоненты в супервершины и рассмотрим граф с этими вершинами и ребрами из второго подмножества. | ||
| + | На последнем шаге останутся две компоненты связности и одно ребро в первом подмножестве — это максимальное ребро минимального веса. | ||
| − | + | На каждом шаге ребер становится в два раза меньше, а все операции выполняются за время пропорциональное количеству ребер на текущем шаге, тогда время работы алгоритма <tex>O(E+\frac{E}{2}+\frac{E}{4}+...+1)=O(E)</tex>. | |
| + | |||
| + | ==Пример== | ||
| + | {| class = "wikitable" | ||
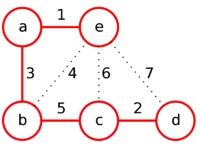
| + | | Рёбра ''(в порядке их просмотра)'' || ae || cd || ab || be || bc || ec || ed | ||
| + | |- | ||
| + | | Веса рёбер ||<tex>1</tex> || <tex>2</tex> || <tex>3</tex> || <tex>4</tex> || <tex>5</tex> || <tex>6</tex> || <tex>7</tex> | ||
| + | |} | ||
| + | |||
| + | {| class = "wikitable" | ||
| + | ! Изображение !! Описание | ||
| + | |- | ||
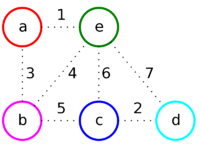
| + | |[[Файл:Mst_kruskal_1.png|200px]] | ||
| + | |style="padding-left: 1em" |Первое ребро, которое будет рассмотрено — '''ae''', так как его вес минимальный.<br/> | ||
| + | Добавим его к ответу, так как его концы соединяют вершины из разных множеств ('''a''' — красное и '''e''' — зелёное).<br/> | ||
| + | Объединим красное и зелёное множество в одно (красное), так как теперь они соединены ребром. | ||
| + | |- | ||
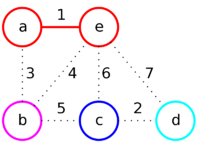
| + | |[[Файл:Mst_kruskal_2.png|200px]] | ||
| + | |style="padding-left: 1em" |Рассмотрим следующие ребро — '''cd'''.<br/> | ||
| + | Добавим его к ответу, так как его концы соединяют вершины из разных множеств ('''c''' — синее и '''d''' — голубое).<br/> | ||
| + | Объединим синее и голубое множество в одно (синее), так как теперь они соединены ребром. | ||
| + | |- | ||
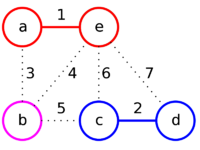
| + | |[[Файл:Mst_kruskal_3.png|200px]] | ||
| + | |style="padding-left: 1em" |Дальше рассмотрим ребро '''ab'''.<br/> | ||
| + | Добавим его к ответу, так как его концы соединяют вершины из разных множеств ('''a''' — красное и '''b''' — розовое).<br/> | ||
| + | Объединим красное и розовое множество в одно (красное), так как теперь они соединены ребром. | ||
| + | |- | ||
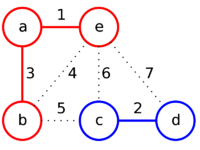
| + | |[[Файл:Mst_kruskal_4.png|200px]] | ||
| + | |style="padding-left: 1em" |Рассмотрим следующие ребро — '''be'''.<br/> | ||
| + | Оно соединяет вершины из одного множества, поэтому перейдём к следующему ребру '''bc'''<br/> | ||
| + | Добавим его к ответу, так как его концы соединяют вершины из разных множеств ('''b''' — красное и '''c''' — синее).<br/> | ||
| + | Объединим красное и синее множество в одно (красное), так как теперь они соединены ребром. | ||
| + | |- | ||
| + | |[[Файл:Mst_kruskal_5.png|200px]] | ||
| + | |style="padding-left: 1em" |Рёбра '''ec''' и '''ed''' соединяют вершины из одного множества,<br/> | ||
| + | поэтому после их просмотра они не будут добавлены в ответ<br/> | ||
| + | Всё рёбра были рассмотрены, поэтому алгоритм завершает работу.<br/> | ||
| + | Полученный граф — минимальное остовное дерево | ||
| + | |} | ||
==Асимптотика== | ==Асимптотика== | ||
Сортировка <tex>E</tex> займет <tex>O(E\log E)</tex>.<br> | Сортировка <tex>E</tex> займет <tex>O(E\log E)</tex>.<br> | ||
| − | Работа с | + | Работа с СНМ займет <tex>O(E\alpha(V))</tex>, где <tex>\alpha</tex> — обратная функция Аккермана, которая не превосходит <tex>4</tex> во всех практических приложениях и которую можно принять за константу.<br> |
| − | Алгоритм работает за <tex>O(E(\log E+\alpha(V))) = O(E\log E | + | Алгоритм работает за <tex>O(E(\log E+\alpha(V))) = O(E\log E)</tex>. |
| − | |||
| − | |||
| − | |||
==См. также== | ==См. также== | ||
* [[Алгоритм Прима]] | * [[Алгоритм Прима]] | ||
| + | * [[Алгоритм Борувки]] | ||
| + | |||
| + | ==Источники информации== | ||
| + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.) | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%90%D0%BA%D0%BA%D0%B5%D1%80%D0%BC%D0%B0%D0%BD%D0%B0 Википедия — Функция Аккермана] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%9A%D1%80%D1%83%D1%81%D0%BA%D0%B0%D0%BB%D0%B0 Википедия — Алгоритм Крускала] | ||
| + | * [http://en.wikipedia.org/wiki/Kruskal's_algorithm Wikipedia — Kruskal's algorithm] | ||
| + | * [http://e-maxx.ru/algo/mst_kruskal MAXimal :: algo :: Минимальное остовное дерево. Алгоритм Крускала] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
| − | [[Категория: Остовные деревья ]] | + | [[Категория: Остовные деревья]] |
| + | [[Категория: Построение остовных деревьев]] | ||
Текущая версия на 19:18, 4 сентября 2022
Алгоритм Краскала (англ. Kruskal's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.
Содержание
Идея
Будем последовательно строить подграф графа ("растущий лес"), пытаясь на каждом шаге достроить до некоторого MST. Начнем с того, что включим в все вершины графа . Теперь будем обходить множество в порядке неубывания весов ребер. Если очередное ребро соединяет вершины одной компоненты связности , то добавление его в остов приведет к возникновению цикла в этой компоненте связности. В таком случае, очевидно, не может быть включено в . Иначе соединяет разные компоненты связности , тогда существует разрез такой, что одна из компонент связности составляет одну его часть, а оставшаяся часть графа — вторую. Тогда — минимальное ребро, пересекающее этот разрез. Значит, из леммы о безопасном ребре следует, что является безопасным, поэтому добавим это ребро в . На последнем шаге ребро соединит две оставшиеся компоненты связности, полученный подграф будет минимальным остовным деревом графа . Для проверки возможности добавления ребра используется система непересекающихся множеств.
Реализация
// — исходный граф // — минимальный остов function for if и в разных компонентах связности return
Задача о максимальном ребре минимального веса
Легко показать, что максимальное ребро в MST минимально. Обратное в общем случае неверно. Но MST из-за сортировки строится за . Однако из-за того, что необходимо минимизировать только максимальное ребро, а не сумму всех рёбер, можно предъявить алгоритм, решающий задачу за линейное время.
С помощью алгоритма поиска k-ой порядковой статистики найдем ребро-медиану за и разделим множество ребер на два равных по мощности так, чтобы ребра в первом не превосходили по весу ребер во втором. Проверим образуют ли ребра из первого подмножества остов графа, запустив обход в глубину.
- Если да, то рекурсивно запустим алгоритм от него.
- В противном случае сконденсируем получившиеся несвязные компоненты в супервершины и рассмотрим граф с этими вершинами и ребрами из второго подмножества.
На последнем шаге останутся две компоненты связности и одно ребро в первом подмножестве — это максимальное ребро минимального веса.
На каждом шаге ребер становится в два раза меньше, а все операции выполняются за время пропорциональное количеству ребер на текущем шаге, тогда время работы алгоритма .
Пример
| Рёбра (в порядке их просмотра) | ae | cd | ab | be | bc | ec | ed |
| Веса рёбер |
Асимптотика
Сортировка займет .
Работа с СНМ займет , где — обратная функция Аккермана, которая не превосходит во всех практических приложениях и которую можно принять за константу.
Алгоритм работает за .
См. также
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
- Википедия — Функция Аккермана
- Википедия — Алгоритм Крускала
- Wikipedia — Kruskal's algorithm
- MAXimal :: algo :: Минимальное остовное дерево. Алгоритм Крускала