Лемма о разрастании для КС-грамматик — различия между версиями
Leugenea (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показана 21 промежуточная версия 9 участников) | |||
| Строка 1: | Строка 1: | ||
| + | __FORCETOC__ | ||
| + | == Лемма о разрастании для КС-грамматик == | ||
| + | |||
{{Лемма | {{Лемма | ||
| − | |id | + | |id=lemma |
|about=о разрастании КС-грамматик | |about=о разрастании КС-грамматик | ||
|statement= | |statement= | ||
| Строка 8: | Строка 11: | ||
Выберем <tex>n=2^{m+1}</tex>. Построим дерево разбора произвольного слова <tex>\omega</tex> длиной больше, чем <tex>n</tex>. Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка <tex>L</tex> записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова <tex>\omega</tex> не меньше <tex>m+1</tex>. | Выберем <tex>n=2^{m+1}</tex>. Построим дерево разбора произвольного слова <tex>\omega</tex> длиной больше, чем <tex>n</tex>. Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка <tex>L</tex> записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова <tex>\omega</tex> не меньше <tex>m+1</tex>. | ||
| − | Количество нетерминалов в нем не меньше, чем <tex>m+1</tex>, следовательно, найдется такой нетерминал <tex>B</tex>, который встречается на этом пути дважды. Значит, в дереве разбора найдется нетерминал <tex>B</tex>, в поддереве которого содержится нетерминал <tex>B</tex>. Выберем нетерминал <tex>A</tex>, | + | Выберем путь от корня дерева к листу максимальной длины. Количество нетерминалов в нем не меньше, чем <tex>m+1</tex>, следовательно, найдется такой нетерминал <tex>B</tex>, который встречается на этом пути дважды. Значит, в дереве разбора найдется нетерминал <tex>B</tex>, в поддереве которого содержится нетерминал <tex>B</tex>. Выберем такой нетерминал <tex>A</tex>, чтобы в его поддереве содержался такой же нетерминал и длина пути от него до корня была максимальна среди всех нетерминалов, содержащих в поддереве такой же нетерминал. |
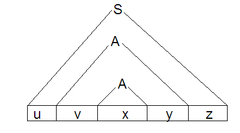
Найдем слова <tex> u,v,x,y,z </tex>. | Найдем слова <tex> u,v,x,y,z </tex>. | ||
| − | *Рассмотрим нетерминал <tex>A</tex>, содержащийся в поддереве выбранного нетерминала. Тогда <tex>x</tex> - строка терминалов которая выведена из рассмотренного нетерминала в данном дереве разбора. <tex>A \Rightarrow^{*} x</tex>. | + | *Рассмотрим нетерминал <tex>A</tex>, содержащийся в поддереве выбранного нетерминала. Тогда <tex>x</tex> {{---}} строка терминалов, которая выведена из рассмотренного нетерминала в данном дереве разбора. Тогда <tex>A \Rightarrow^{*} x</tex>. |
| − | *Рассмотрим выбранный нетерминал <tex>A</tex>. Пусть <tex>t</tex> - строка терминальных символов, которая выведена из рассмотренного нетерминала в данном дереве разбора. Тогда <tex>A \Rightarrow^{*}\alpha A \beta \Rightarrow^{*} t</tex>, где <tex>\alpha,\beta</tex> - строки | + | *Рассмотрим выбранный ранее нетерминал <tex>A</tex>. Пусть <tex>t</tex> {{---}} строка терминальных символов, которая выведена из рассмотренного нетерминала в данном дереве разбора. Тогда, так как выбранный нетерминал <tex>A</tex> содержит в своем поддереве такой же нетерминал, то <tex>A \Rightarrow^{*}\alpha A \beta \Rightarrow^{*} t</tex>, где <tex>\alpha,\beta</tex> - строки, которые могут содержать как терминалы, так и нетерминалы. При этом как минимум одна из строк <tex>\alpha,\beta</tex> не пуста, так как грамматика языка записана в НФХ. Пусть <tex>v</tex> и <tex>y</tex> - строки, состоящие из терминалов, которые выведены соответственно из <tex>\alpha</tex> и <tex>\beta</tex>, в данном дереве разбора. Тогда <tex>t = vxy</tex>. Так как хотя бы одна из строк <tex>\alpha,\beta</tex> не пуста, то <tex>vy\neq \varepsilon</tex>. Получаем <tex>A \Rightarrow^{*} vAy \Rightarrow^{*} vxy</tex>. |
| − | *Рассмотрим стартовый нетерминал <tex>S</tex>. Из <tex>S</tex> выведена строка <tex>\omega</tex>. При этом <tex>S \Rightarrow^{*} \alpha A \beta \Rightarrow^{*} \omega </tex>, где <tex>A</tex> - выбранный ранее нетерминал. Из <tex>A</tex> в данном дереве разбора выведена строка <tex>vxy</tex>. Пусть <tex>u | + | *Рассмотрим стартовый нетерминал <tex>S</tex>. Из <tex>S</tex> выведена строка <tex>\omega</tex>. При этом <tex>S \Rightarrow^{*} \alpha A \beta \Rightarrow^{*} \omega </tex>, где <tex>A</tex> {{---}} выбранный ранее нетерминал. Из <tex>A</tex> в данном дереве разбора выведена строка <tex>vxy</tex>. Пусть <tex>u</tex> и <tex>z</tex> {{---}} строки, состоящие из терминалов, которые выведены соответственно из <tex>\alpha</tex> и <tex>\beta</tex> в данном дереве разбора. Тогда <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} \omega</tex>. |
| + | Покажем, что <tex>|vxy| \leqslant n</tex>. Допустим, что <tex>|vxy|>n</tex>. Тогда высота поддерева с корнем в вершине, соответствующей выбранному <tex>A</tex>, не меньше <tex>m+2</tex>. Рассмотрим поддерево вершины, в котором содержится нетерминал <tex>A</tex>. Тогда высота этого поддерева не меньше <tex>m+1</tex>. Рассмотрим путь максимальной длины от корня этого поддерева к листу. В нем содержится не менее <tex>m+1</tex> нетерминалов, причем не содержится стартовый нетерминал. Следовательно, на этом пути найдутся два одинаковых нетерминала, что противоречит условию наибольшей удаленности от корня выбранного ранее нетерминала <tex>A</tex>. Получили противоречие. Поэтому <tex>|vxy|\leqslant n</tex>. | ||
Таким образом, в рамках нашей грамматики мы можем построить цепочку вывода: <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | Таким образом, в рамках нашей грамматики мы можем построить цепочку вывода: <tex>S \Rightarrow^{*} uAz \Rightarrow^{*} uvAyz \Rightarrow^{*} uvvAyyz \Rightarrow^{*} uv^{k}Ay^{k}z \Rightarrow^{*} uv^{k}xy^{k}z</tex>. | ||
}} | }} | ||
| − | '''Замечание.''' Условие леммы не является достаточным для контекстно-свободности языка. Но в силу необходимости, данная лемма часто используется для доказательства неконтекстно-свободности языков. | + | '''Замечание.''' Условие леммы не является достаточным для контекстно-свободности языка. Но, в силу необходимости условия, данная лемма часто используется для доказательства неконтекстно-свободности языков. |
| + | |||
| + | == Пример доказательства неконтекстно-свободности языка с использованием леммы == | ||
| + | |||
| + | Рассмотрим язык <tex>0^{n}1^{n}2^{n}</tex>. Покажем, что он не является контекстно-свободным. | ||
| + | |||
| + | Для фиксированного <tex>n</tex> рассмотрим слово <tex>\omega=0^n 1^n 2^n</tex>. Пусть <tex>\omega</tex> разбили на <tex>u, v, x, y, z</tex> произвольным образом. Так как <tex>|vxy|\leqslant n</tex>, то в слове <tex>vxy</tex> не содержится либо ни одного символа <tex>0</tex>, либо ни одного символа <tex>2</tex>. Для любого такого разбиения выбираем <tex>k=2</tex> и получаем, что количество символов <tex>1</tex> изменилось, а количество либо <tex>0</tex>, либо <tex>2</tex> осталось тем же. Очевидно, что такое слово не принадлежит рассмотренному языку. Значит, язык <tex>0^{n}1^{n}2^{n}</tex> не является контекстно-свободным по лемме о разрастании для КС-грамматик. | ||
| + | |||
| + | == Пример не КС-языка, для которого выполняется лемма == | ||
| + | |||
| + | Рассмотрю язык <tex>L=\{a^{n}b^{n}c^{i}\mid i \neq n\}</tex>. | ||
| + | |||
| + | '''Докажем, что он не контекстно-свободный'''. Для этого воспользуемся [[Лемма_Огдена|леммой Огдена]]. Для фиксированного <tex>n</tex> рассмотрим слово <tex>\omega=a^n b^n c^{n!+n}</tex>. Пометим все символы <tex>a</tex> и <tex>b</tex>. Пусть <tex>\omega</tex> разбили на <tex>u, v, x, y, z</tex>, так что <tex>x</tex> содержит выделенную позицию; <tex>u</tex> и <tex>v</tex> содержат выделенные позиции и <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций. Тогда очевидно, что <tex>vy</tex> должно содержать одинаковое число символов <tex>a</tex> и <tex>b</tex>, иначе выбираем <tex>k=0</tex> и тогда количество символов <tex>a</tex> и <tex>b</tex> станет разным. Пусть символов <tex>a</tex> в <tex>vy</tex> будет <tex>t</tex>. Так же очевидно, что <tex>vy</tex> не содержит символов <tex>c</tex>, так как <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций, но <tex>v</tex> точно содержит символ <tex>a</tex>. Тогда выберем <tex>k=\dfrac{n!}{t}+1</tex> и получим слово <tex>a^{n!+n}b^{n!+n}c^{n!+n}</tex>, которое не принадлежит рассмотренному языку. Значит <tex>a^{n}b^{n}c^{i}</tex> не является контекстно-свободным. | ||
| + | |||
| + | '''Докажем, что язык удовлетворяет лемме о разрастании'''. Выберем <tex>n=5</tex>. Это значит, что длина рассматриваемых слов не меньше <tex>3</tex>. Рассмотрим случаи: | ||
| + | # <tex>c^i</tex> | ||
| + | #:Выберем <tex>u=c^{i-1}</tex>, <tex>v=c</tex>, <tex>x=y=z=\varepsilon</tex>. | ||
| + | # <tex>a^jb^j</tex> | ||
| + | #:Выберем <tex>u=a^{j-1}</tex>, <tex>v=a</tex>, <tex>x=\varepsilon</tex>, <tex>y=b</tex>, <tex>z=b^{j-1}</tex>. | ||
| + | # <tex>a^jb^jc^i</tex>, где <tex>i < j-1</tex> | ||
| + | #:Выберем <tex>u=a^{j-1}</tex>, <tex>v=a</tex>, <tex>x=\varepsilon</tex>, <tex>y=b</tex>, <tex>z=b^{j-1}c^i</tex>. | ||
| + | # <tex>a^jb^jc^{j-1}</tex> | ||
| + | #:Выберем <tex>u=a^{j-2}</tex>, <tex>v=aa</tex>, <tex>x=\varepsilon</tex>, <tex>y=bb</tex>, <tex>z=b^{j-2}c^i</tex>. | ||
| + | # <tex>a^jb^jc^{j+1}</tex> | ||
| + | #:Выберем <tex>u=a^{j-2}</tex>, <tex>v=aa</tex>, <tex>x=\varepsilon</tex>, <tex>y=bb</tex>, <tex>z=b^{j-2}c^i</tex>. | ||
| + | # <tex>a^jb^jc^i</tex>, где <tex>i>j+1</tex> | ||
| + | #:Выберем <tex>u=a^jb^jc^{i-1}</tex>, <tex>v=c</tex>, <tex>x=y=z=\varepsilon</tex>. | ||
| + | |||
| + | Таким образом язык <tex>L</tex> '''не''' контекстно-свободный, но удовлетворяет второй части леммы. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Лемма_Огдена|Лемма Огдена]] | ||
| + | |||
| + | == Источники == | ||
| + | |||
| + | * Хопкрофт Д., Мотвани Р., Ульман Д. {{---}} Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. {{---}} Москва, Издательский дом «Вильямс», 2002. {{---}} 528 с. : ISBN 5-8459-0261-4 (рус.) | ||
| − | + | [[Категория: Теория формальных языков]] | |
| − | + | [[Категория: Контекстно-свободные грамматики]] | |
| + | [[Категория: Опровержение контекстно-свободности языка]] | ||
Текущая версия на 19:37, 4 сентября 2022
Содержание
Лемма о разрастании для КС-грамматик
| Лемма (о разрастании КС-грамматик): |
Пусть — контекстно-свободный язык над алфавитом , тогда существует такое , что для любого слова длины не меньше найдутся слова , для которых верно: и . |
| Доказательство: |
|
Грамматика любого контекстно-свободного языка может быть записана в нормальной форме Хомского (НФХ). Пусть — количество нетерминалов в грамматике языка , записанной в НФХ.
Выберем . Построим дерево разбора произвольного слова длиной больше, чем . Высотой дерева разбора назовем максимальное число нетерминальных символов на пути от корня дерева к листу. Так как грамматика языка записана в НФХ, то у любого нетерминала в дереве могут быть, либо два потомка нетерминала, либо один потомок терминал. Поэтому высота дерева разбора слова не меньше . Выберем путь от корня дерева к листу максимальной длины. Количество нетерминалов в нем не меньше, чем , следовательно, найдется такой нетерминал , который встречается на этом пути дважды. Значит, в дереве разбора найдется нетерминал , в поддереве которого содержится нетерминал . Выберем такой нетерминал , чтобы в его поддереве содержался такой же нетерминал и длина пути от него до корня была максимальна среди всех нетерминалов, содержащих в поддереве такой же нетерминал. Найдем слова .
Покажем, что . Допустим, что . Тогда высота поддерева с корнем в вершине, соответствующей выбранному , не меньше . Рассмотрим поддерево вершины, в котором содержится нетерминал . Тогда высота этого поддерева не меньше . Рассмотрим путь максимальной длины от корня этого поддерева к листу. В нем содержится не менее нетерминалов, причем не содержится стартовый нетерминал. Следовательно, на этом пути найдутся два одинаковых нетерминала, что противоречит условию наибольшей удаленности от корня выбранного ранее нетерминала . Получили противоречие. Поэтому . Таким образом, в рамках нашей грамматики мы можем построить цепочку вывода: . |
Замечание. Условие леммы не является достаточным для контекстно-свободности языка. Но, в силу необходимости условия, данная лемма часто используется для доказательства неконтекстно-свободности языков.
Пример доказательства неконтекстно-свободности языка с использованием леммы
Рассмотрим язык . Покажем, что он не является контекстно-свободным.
Для фиксированного рассмотрим слово . Пусть разбили на произвольным образом. Так как , то в слове не содержится либо ни одного символа , либо ни одного символа . Для любого такого разбиения выбираем и получаем, что количество символов изменилось, а количество либо , либо осталось тем же. Очевидно, что такое слово не принадлежит рассмотренному языку. Значит, язык не является контекстно-свободным по лемме о разрастании для КС-грамматик.
Пример не КС-языка, для которого выполняется лемма
Рассмотрю язык .
Докажем, что он не контекстно-свободный. Для этого воспользуемся леммой Огдена. Для фиксированного рассмотрим слово . Пометим все символы и . Пусть разбили на , так что содержит выделенную позицию; и содержат выделенные позиции и содержат не более выделенных позиций. Тогда очевидно, что должно содержать одинаковое число символов и , иначе выбираем и тогда количество символов и станет разным. Пусть символов в будет . Так же очевидно, что не содержит символов , так как содержат не более выделенных позиций, но точно содержит символ . Тогда выберем и получим слово , которое не принадлежит рассмотренному языку. Значит не является контекстно-свободным.
Докажем, что язык удовлетворяет лемме о разрастании. Выберем . Это значит, что длина рассматриваемых слов не меньше . Рассмотрим случаи:
-
- Выберем , , .
-
- Выберем , , , , .
- , где
- Выберем , , , , .
-
- Выберем , , , , .
-
- Выберем , , , , .
- , где
- Выберем , , .
Таким образом язык не контекстно-свободный, но удовлетворяет второй части леммы.
См. также
Источники
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)