Эргодическая марковская цепь — различия между версиями
Whiplash (обсуждение | вклад) м (→Ссылки) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 16 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Эргодическая''' [[Марковская цепь|марковская цепь]] {{---}} марковская цепь, целиком состоящая из одного эргодического класса. | + | '''Эргодическая''' [[Марковская цепь|марковская цепь]] (англ. ''ergodic Markov chain'') {{---}} марковская цепь, целиком состоящая из одного [[Марковская цепь#sort_def| эргодического класса]]. |
}} | }} | ||
==Стационарный режим== | ==Стационарный режим== | ||
| − | Эргодические марковские цепи описываются [[Отношение связности, компоненты связности|сильно связным графом]]. Это означает, что в такой системе возможен переход из любого состояния <tex>S_i</tex> в любое состояние <tex>S_{j}, (i,j = 1,2, | + | Эргодические марковские цепи описываются [[Отношение связности, компоненты связности|сильно связным графом]]. Это означает, что в такой системе возможен переход из любого состояния <tex>S_i</tex> в любое состояние <tex>S_{j}, (i,j = 1,2,\ldots,n)</tex> за конечное число шагов. |
| − | Для эргодических цепей при достаточно большом времени функционирования (<tex>t \to \infty</tex>) наступает '''стационарный режим''', при котором вероятности <tex>\alpha_i</tex> состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, | + | Для эргодических цепей при достаточно большом времени функционирования (<tex>t \to \infty</tex>) наступает '''стационарный режим''', при котором вероятности <tex>\alpha_i</tex> состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, то есть: <tex>\alpha_i = const</tex>. |
== Классификация эргодических цепей == | == Классификация эргодических цепей == | ||
| Строка 13: | Строка 13: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | В эргодической цепи можно выделить '''циклические классы'''. Количество циклических классов <tex> d </tex> называют '''периодом цепи''', если цепь состоит целиком из одного циклического класса, её называют [[Регулярная марковская цепь|регулярной]]. С течением времени текущее состояние движется по циклическим классам в определенном порядке, причем каждые | + | В эргодической цепи можно выделить '''циклические классы''' (англ. ''cyclic classes''). Количество циклических классов <tex> d </tex> называют '''периодом цепи''' (англ. ''period of Markov chain''), если цепь состоит целиком из одного циклического класса, её называют [[Регулярная марковская цепь|регулярной]]. С течением времени текущее состояние движется по циклическим классам в определенном порядке, причем каждые <tex>d</tex> шагов она оказывается в одном и том же циклическом классе. |
}} | }} | ||
| Строка 21: | Строка 21: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Эргодическое (стационарное) распределение''' - распределение <tex>\alpha = (\alpha_1 \ | + | '''Эргодическое (стационарное) распределение''' (англ. ''stationary distribution'') {{---}} распределение <tex>\alpha = (\alpha_1 \ldots \alpha_n )</tex>, такое что <tex>\alpha_i > 0</tex> и |
| − | <tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \alpha_j</tex> (где <tex>p_{ij}^{(n)}</tex> - вероятность оказаться в <tex>j</tex>-ом состоянии, выйдя из <tex>i</tex>-ого, через <tex>n</tex> переходов). | + | <tex>\lim\limits_{n \to \infty} p_{ij}^{(n)} = \alpha_j</tex> (где <tex>p_{ij}^{(n)}</tex> {{---}} вероятность оказаться в <tex>j</tex>-ом состоянии, выйдя из <tex>i</tex>-ого, через <tex>n</tex> переходов). |
}} | }} | ||
| Строка 33: | Строка 33: | ||
|about=Эргодическая теорема | |about=Эргодическая теорема | ||
|statement= | |statement= | ||
| − | Для любой эргодической цепи последовательность степеней <tex>P^{n}</tex> суммируется по Эйлеру к предельной матрице <tex>A</tex>, и эта предельная матрица имеет вид <tex>A = \xi\alpha</tex>, где <tex>\alpha</tex> - положительный вероятностный вектор, <tex>\xi</tex> - вектор-столбец из единиц. | + | Для любой эргодической цепи последовательность степеней <tex>P^{n}</tex> [http://en.wikipedia.org/wiki/Euler_summation суммируется по Эйлеру] к предельной матрице <tex>A</tex>, и эта предельная матрица имеет вид <tex>A = \xi\alpha</tex>, где <tex>\alpha</tex> {{---}} положительный вероятностный вектор, <tex>\xi</tex> - вектор-столбец из единиц. |
|proof= | |proof= | ||
| Строка 41: | Строка 41: | ||
Рассмотрим матрицу <tex>(kI + (1 - k)P)</tex> при некотором <tex>k, ~ 0 < k < 1</tex>. Эта матрица является ''переходной матрицей''. Она имеет положительные элементы на всех тех же местах, что и <tex>P</tex>, следовательно, она также ''задает эргодическую цепь''. Также диагональные элементы этой матрицы положительны. Значит, в каждое состояние можно возвратиться за один шаг, а это значит, что <tex>d = 1</tex>. Таким образом, новая цепь является регулярной. | Рассмотрим матрицу <tex>(kI + (1 - k)P)</tex> при некотором <tex>k, ~ 0 < k < 1</tex>. Эта матрица является ''переходной матрицей''. Она имеет положительные элементы на всех тех же местах, что и <tex>P</tex>, следовательно, она также ''задает эргодическую цепь''. Также диагональные элементы этой матрицы положительны. Значит, в каждое состояние можно возвратиться за один шаг, а это значит, что <tex>d = 1</tex>. Таким образом, новая цепь является регулярной. | ||
| − | Из [[Регулярная марковская цепь#Эргодическая теорема для регулярных цепей | эргодической теоремы для регулярных цепей]] следует, что <tex>(kI + (1 - k)P)^{n}</tex> стремится к матрице <tex>A = \xi\alpha</tex>, где <tex>\alpha</tex> - положительный вероятностный вектор. Таким образом: | + | Из [[Регулярная марковская цепь#Эргодическая теорема для регулярных цепей | эргодической теоремы для регулярных цепей]] следует, что <tex>(kI + (1 - k)P)^{n}</tex> стремится к матрице <tex>A = \xi\alpha</tex>, где <tex>\alpha</tex> {{---}} положительный вероятностный вектор. Таким образом: |
: <tex> A = \lim\limits_{x\to \infty} (kI + (1 - k)P)^{n}</tex> | : <tex> A = \lim\limits_{x\to \infty} (kI + (1 - k)P)^{n}</tex> | ||
: <tex> A = \lim\limits_{x\to \infty} \sum\limits_{i = 0}^{n} {n\choose i} k^{n - i} (1 - k)^{i} P^{i} ~~~~~ (1)</tex> | : <tex> A = \lim\limits_{x\to \infty} \sum\limits_{i = 0}^{n} {n\choose i} k^{n - i} (1 - k)^{i} P^{i} ~~~~~ (1)</tex> | ||
| Строка 50: | Строка 50: | ||
{{Теорема | {{Теорема | ||
| − | |statement=Если <tex>P, A, \alpha</tex> - объекты из предыдущей теоремы. Тогда справедливы факты: | + | |statement=Если <tex>P, A, \alpha</tex> {{---}} объекты из предыдущей теоремы. Тогда справедливы факты: |
* Для любого вероятностного вектора <tex>\pi</tex> последовательность <tex>\pi P^{n}</tex> суммируема по Эйлеру к <tex>\alpha</tex> | * Для любого вероятностного вектора <tex>\pi</tex> последовательность <tex>\pi P^{n}</tex> суммируема по Эйлеру к <tex>\alpha</tex> | ||
| Строка 79: | Строка 79: | ||
Стационарным распределением этой цепи будет <tex> \alpha = (0.5, 0.5) </tex>. | Стационарным распределением этой цепи будет <tex> \alpha = (0.5, 0.5) </tex>. | ||
| − | == | + | ==См. также== |
| − | *[ | + | *[[Марковская цепь]] |
| + | *[[Регулярная марковская цепь]] | ||
| + | *[[Примеры использования Марковских цепей]] | ||
| − | + | == Источники информации == | |
| − | *[http://en.wikipedia.org/wiki/Euler_summation | + | *[http://ru.wikipedia.org/wiki/Эргодическое_распределение Википедия {{---}} Эргодическое распределение ] |
| − | + | *[http://ru.wikipedia.org/wiki/Дискретное_распределение#.D0.94.D0.B8.D1.81.D0.BA.D1.80.D0.B5.D1.82.D0.BD.D1.8B.D0.B5_.D1.80.D0.B0.D1.81.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F Википедия {{---}} Дискретное распределение] | |
| − | + | *[http://en.wikipedia.org/wiki/Euler_summation Wikipedia {{---}} Euler summation] | |
| − | Дж. Кемени, Дж. Снелл | + | *Дж. Кемени, Дж. Снелл {{---}} Конечные цепи Маркова {{---}} изд. "Наука", 1970 г. {{---}} 129 c. |
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
| − | [[Категория: Марковские цепи ]] | + | [[Категория: Марковские цепи]] |
Текущая версия на 19:15, 4 сентября 2022
| Определение: |
| Эргодическая марковская цепь (англ. ergodic Markov chain) — марковская цепь, целиком состоящая из одного эргодического класса. |
Стационарный режим
Эргодические марковские цепи описываются сильно связным графом. Это означает, что в такой системе возможен переход из любого состояния в любое состояние за конечное число шагов.
Для эргодических цепей при достаточно большом времени функционирования () наступает стационарный режим, при котором вероятности состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, то есть: .
Классификация эргодических цепей
| Определение: |
| В эргодической цепи можно выделить циклические классы (англ. cyclic classes). Количество циклических классов называют периодом цепи (англ. period of Markov chain), если цепь состоит целиком из одного циклического класса, её называют регулярной. С течением времени текущее состояние движется по циклическим классам в определенном порядке, причем каждые шагов она оказывается в одном и том же циклическом классе. |
Таким образом, эргодические цепи делятся на регулярные и циклические.
Эргодическая теорема
| Определение: |
| Эргодическое (стационарное) распределение (англ. stationary distribution) — распределение , такое что и (где — вероятность оказаться в -ом состоянии, выйдя из -ого, через переходов). |
Для регулярных цепей
Доказательство теоремы для случая регулярных цепей приведено в конспекте про регулярные цепи.
Для циклических цепей
| Теорема (Эргодическая теорема): |
Для любой эргодической цепи последовательность степеней суммируется по Эйлеру к предельной матрице , и эта предельная матрица имеет вид , где — положительный вероятностный вектор, - вектор-столбец из единиц. |
| Доказательство: |
|
В случае циклической цепи переходы из одного циклического класса в другой возможны только при определенных значениях , которые периодически повторяются. Таким образом, никакая степень матрицы переходов не является положительной матрицей, и различные степени содержат нули на различных местах. С увеличением степени расположение этих нулей периодически повторяется. Следовательно, последовательность не может сходиться в обычном смысле, для нее требуется так называемая суммируемость по Эйлеру. Рассмотрим матрицу при некотором . Эта матрица является переходной матрицей. Она имеет положительные элементы на всех тех же местах, что и , следовательно, она также задает эргодическую цепь. Также диагональные элементы этой матрицы положительны. Значит, в каждое состояние можно возвратиться за один шаг, а это значит, что . Таким образом, новая цепь является регулярной. Из эргодической теоремы для регулярных цепей следует, что стремится к матрице , где — положительный вероятностный вектор. Таким образом: |
Следствия
| Теорема: |
Если — объекты из предыдущей теоремы. Тогда справедливы факты:
|
| Доказательство: |
|
Домножим на . Таким образом, мы получим, что предел последовательности в смысле Эйлера равен . Значит, первый факт доказан.
следует, что и поскольку , то . Получается, что второй факт доказан.
|
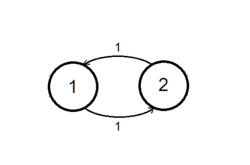
Пример
Самым простым примером циклической цепи является цепь из двух состояний, с переходной матрицей:
- .
Стационарным распределением этой цепи будет .
См. также
Источники информации
- Википедия — Эргодическое распределение
- Википедия — Дискретное распределение
- Wikipedia — Euler summation
- Дж. Кемени, Дж. Снелл — Конечные цепи Маркова — изд. "Наука", 1970 г. — 129 c.