Задача обедающих философов — различия между версиями
(Новая страница: «==Задача обедающих философов== за круглым столом сидят шесть философов. На столе шесть таре…») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 18 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Категория: Параллельное программирование]] | ||
==Задача обедающих философов== | ==Задача обедающих философов== | ||
| − | + | За круглым столом сидят шесть философов (процессы). На столе шесть тарелок с рисом и шесть вилок. | |
| − | В каждый момент философ может либо есть (тогда ему необходимо две | + | |
| + | В каждый момент философ может либо хотеть есть (тогда ему необходимо две вилки), либо хотеть думать (для этого ему нужен только он сам). | ||
| + | Философы не разговаривают между собой (только в начале, когда договариваются об алгоритме). Необходимо, чтобы все философы поели и не возникло драки за вилки. | ||
==Обобщение== | ==Обобщение== | ||
| − | + | В случае с философами у нас есть $N$ процессов и граф конфликтов между ними из $N$ рёбер (одно ребро — один общий для двух процессов ресурс). Процессу для работы надо собрать все конфликтующие с другими потоками ресурсы. | |
| + | |||
| + | А взаимное исключение — это полный граф конфликтов, т.е есть вилка для каждой пары философов. | ||
| + | Так что алгоритм для философов можно использовать и для задачи взаимного исключения. | ||
| + | |||
| + | ==Решение== | ||
| + | |||
| + | |||
| + | ===Алгоритм обедающих философов=== | ||
| + | Как построить алгоритм (вроде описан в "The Drinking Philosophers Problem" от K.M.Chandy и K.Misra): | ||
| + | |||
| + | # Ориентируем граф конфликтов так, чтобы он стал ациклическим. Например, по результатам сравнения id философов. Ориентация ребра задаёт, у кого вилка. Так как в ациклическом графе есть исток, то хотя бы у кого-то все вилки есть. А когда поест, то можно перевернуть все рёбра у истока, тогда граф останется ациклическим. Если предположить, что философы всегда хотят есть (но едят конечное количество времени), то философы будут бесконечно есть. | ||
| + | # Заметим, что голодания ни у кого нет: возьмём множество вершин, которые будут есть бесконечное количество раз. Тогда заметим, что если есть ребро между этим множеством и его дополнением, то рано или поздно это ребро начнёт вести из этого множества и не будет переключаться обратно (так как для переключения обратно надо, чтобы процесс из дополнения поел). А значит, что его конец в множестве тоже не может бесконечно много есть. Противоречие. Стало быть, это множество — компонента связности графа конфликтов. | ||
| + | # Теперь можно сэкономить сообщения, если кто-то есть не хочет. Для этого не будем сразу после еды отдавать вилку, а будем помечать её "грязной" и отдавать, только если наш сосед её явно попросит. А если снова захотели есть, то надо сначала попросить все вилки у соседей (и не отдавать, пока не поедим), а только потом помыть грязные: пока будем просить у соседей, грязные могут отобрать. Если бы мы их просто так помыли и не отдавали, то будет deadlock уже при N=3. | ||
| + | |||
| + | Другое описание: | ||
| + | |||
| + | # Все соседние вилки должны быть чистые, чтобы философ мог войти в критическую секцию. | ||
| + | # После еды он должен отдать вилки, но мы не будем тратить сообщения на их передачу. Просто помечаем, что вилки грязные. | ||
| + | # При запросе соседа-философа будем мыть совместную вилку (делать ее чистой) и отдавать ее, даже если сами хотим есть. | ||
| + | # При получении запроса на вилку, чистые вилки отдавать не будем. | ||
| + | |||
| + | Итого: | ||
| + | * 0 сообщений на повторный заход в CS одним философом (процессом); | ||
| + | * 2N-2 сообщений в худшем случае; | ||
| + | * Количество сообщений пропорционально числу процессов, которые хотят попасть в критическую секцию. | ||
===Token ring=== | ===Token ring=== | ||
| Строка 12: | Строка 40: | ||
То есть, если ни один из процессов не заинтересован в критической секции, то маркер будет просто циркулировать по кольцу. | То есть, если ни один из процессов не заинтересован в критической секции, то маркер будет просто циркулировать по кольцу. | ||
| + | |||
| + | [[Файл:mutex-distributed-token.png|400px]] | ||
Текущая версия на 19:22, 4 сентября 2022
Содержание
Задача обедающих философов
За круглым столом сидят шесть философов (процессы). На столе шесть тарелок с рисом и шесть вилок.
В каждый момент философ может либо хотеть есть (тогда ему необходимо две вилки), либо хотеть думать (для этого ему нужен только он сам). Философы не разговаривают между собой (только в начале, когда договариваются об алгоритме). Необходимо, чтобы все философы поели и не возникло драки за вилки.
Обобщение
В случае с философами у нас есть $N$ процессов и граф конфликтов между ними из $N$ рёбер (одно ребро — один общий для двух процессов ресурс). Процессу для работы надо собрать все конфликтующие с другими потоками ресурсы.
А взаимное исключение — это полный граф конфликтов, т.е есть вилка для каждой пары философов. Так что алгоритм для философов можно использовать и для задачи взаимного исключения.
Решение
Алгоритм обедающих философов
Как построить алгоритм (вроде описан в "The Drinking Philosophers Problem" от K.M.Chandy и K.Misra):
- Ориентируем граф конфликтов так, чтобы он стал ациклическим. Например, по результатам сравнения id философов. Ориентация ребра задаёт, у кого вилка. Так как в ациклическом графе есть исток, то хотя бы у кого-то все вилки есть. А когда поест, то можно перевернуть все рёбра у истока, тогда граф останется ациклическим. Если предположить, что философы всегда хотят есть (но едят конечное количество времени), то философы будут бесконечно есть.
- Заметим, что голодания ни у кого нет: возьмём множество вершин, которые будут есть бесконечное количество раз. Тогда заметим, что если есть ребро между этим множеством и его дополнением, то рано или поздно это ребро начнёт вести из этого множества и не будет переключаться обратно (так как для переключения обратно надо, чтобы процесс из дополнения поел). А значит, что его конец в множестве тоже не может бесконечно много есть. Противоречие. Стало быть, это множество — компонента связности графа конфликтов.
- Теперь можно сэкономить сообщения, если кто-то есть не хочет. Для этого не будем сразу после еды отдавать вилку, а будем помечать её "грязной" и отдавать, только если наш сосед её явно попросит. А если снова захотели есть, то надо сначала попросить все вилки у соседей (и не отдавать, пока не поедим), а только потом помыть грязные: пока будем просить у соседей, грязные могут отобрать. Если бы мы их просто так помыли и не отдавали, то будет deadlock уже при N=3.
Другое описание:
- Все соседние вилки должны быть чистые, чтобы философ мог войти в критическую секцию.
- После еды он должен отдать вилки, но мы не будем тратить сообщения на их передачу. Просто помечаем, что вилки грязные.
- При запросе соседа-философа будем мыть совместную вилку (делать ее чистой) и отдавать ее, даже если сами хотим есть.
- При получении запроса на вилку, чистые вилки отдавать не будем.
Итого:
- 0 сообщений на повторный заход в CS одним философом (процессом);
- 2N-2 сообщений в худшем случае;
- Количество сообщений пропорционально числу процессов, которые хотят попасть в критическую секцию.
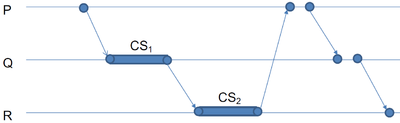
Token ring
Все процессы объединяются в логическое кольцо независимо от реальной структуры сети.
По кольцу передается маркер (token). Процесс, получивший маркер, проверяет, нужно ли ему войти в критическую секцию. Если нужно, то входит, а после ее завершения отправляет маркер дальше по кольцу. Если не нужно, то сразу отправляет маркер дальше.
То есть, если ни один из процессов не заинтересован в критической секции, то маркер будет просто циркулировать по кольцу.