СНМ (наивные реализации) — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 45 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Система (лес, объединение) непересекающихся множеств''' (СНМ, disjoint set forest, DSF, disjoint set union, DSU) {{---}} иерархическая структура данных, позволяющая эффективно работать с множествами. | |
| − | + | __TOC__ | |
| − | Система непересекающихся множеств (disjoint set union, DSU) {{ --- }} структура данных, | + | == Описание == |
| − | + | Структура хранит набор объектов (например, чисел от <tex> 0 </tex> до <tex> n - 1 </tex>) в виде непересекающихся множеств. У каждого множества есть конкретный представитель. | |
| − | + | Определены две операции: | |
| + | * <math> \mathrm{union(x, y)} </math> {{ --- }} объединяет множества, содержащие <tex> x </tex> и <tex> y </tex> | ||
| + | * <math> \mathrm{find (x)} </math> {{ --- }} возвращает представителя множества, в котором находится <tex> x </tex> | ||
| + | Для любого элемента множества представитель всегда одинаковый. Поэтому чтобы проверить принадлежность элементов <tex> x </tex> и <tex> y </tex> одному множеству достаточно сравнить <math> \mathrm{find (x)} </math> и <math> \mathrm{find(y)} </math>. | ||
| − | + | [[Файл:DSU_1_Example.png|500px|center|Пример работы СНМ]] | |
| − | [[Файл:DSU_1_Example.png| | ||
== Реализации == | == Реализации == | ||
=== С помощью массива === | === С помощью массива === | ||
| + | |||
| + | <!-- | ||
'''Оценка работы:''' | '''Оценка работы:''' | ||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
| Строка 21: | Строка 25: | ||
|<tex>O(n)</tex> | |<tex>O(n)</tex> | ||
|} | |} | ||
| − | |||
--> | --> | ||
| − | |||
| − | + | Пусть в массиве s хранятся номера множеств, в <tex> s[i] </tex> будет храниться номер множества, к которому принадлежит <tex> i </tex>. Этот номер отождествляет множество, <math> \mathrm{find} </math> возвращает именно его. Тогда <math> \mathrm{find} </math>, очевидно, будет работать за <tex>O(1)</tex>. | |
| − | ''' | + | Чтобы объединить множества <tex> x </tex> и <tex> y </tex>, надо изменить все <tex> s[i] </tex>, равные номеру множества <tex> x </tex>, на номер <tex> y </tex>. Тогда <math> \mathrm{union} </math> работает за <tex>O(n)</tex>. |
| − | + | ||
| − | init(): | + | '''int''' s[n] |
| − | for i = 0 to n - 1 | + | '''func''' init(): |
| − | s[i] = i // сначала каждый элемент лежит в своем множестве | + | '''for''' i = 0 '''to''' n - 1 |
| − | + | s[i] = i <font color=green> // сначала каждый элемент лежит в своем множестве </font> | |
| − | find(k): | + | |
| − | return s[k] | + | '''int''' find(k): |
| − | + | '''return''' s[k] | |
| − | union(x, y): | + | |
| − | if s[x] == s[y] | + | '''func''' union(x, y): |
| − | return | + | '''if''' s[x] == s[y] |
| − | else | + | '''return''' |
| + | '''else''' | ||
t = s[y] | t = s[y] | ||
| − | for i = 0 to n - 1 | + | '''for''' i = 0 '''to''' n - 1 |
| − | if s[i] == t | + | '''if''' s[i] == t |
s[i] = s[x] | s[i] = s[x] | ||
=== С помощью списка === | === С помощью списка === | ||
| − | '''Оценка работы:''' | + | <!--'''Оценка работы:''' |
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|init | |init | ||
| Строка 55: | Строка 58: | ||
|<tex>O(n)</tex> | |<tex>O(n)</tex> | ||
|<tex>O(1)</tex> | |<tex>O(1)</tex> | ||
| − | |} | + | |}--> |
| − | |||
| − | Для того | + | Будем хранить множество в виде списка. Для каждого элемента списка храним ссылку на следующий элемент и указатель на <tex> head </tex>, который является представителем. Для того чтобы найти представителя, нужно перейти по ссылке на <tex> head </tex>. Значит <math> \mathrm{find} </math> работает за <tex> O(1) </tex>. |
| − | + | Для объединения множеств потребуется объединить два списка и обновить ссылки на <tex> head </tex>. Таким образом, <math> \mathrm{union} </math> работает за <tex> O(n) </tex>. | |
| − | + | Чтобы объединить два списка, нужно хранить ссылку на <tex> tail </tex>. Ее можно хранить в голове списка. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''struct''' SetItem |
| + | '''int''' data | ||
| + | '''SetItem''' head | ||
| + | '''SetItem''' next | ||
| + | '''SetItem''' tail | ||
| − | + | '''SetItem''' s[n] | |
| − | [[ | + | '''func''' init(): |
| + | '''for''' i = 0 '''to''' n - 1 | ||
| + | s[i].data = i | ||
| + | s[i].head = s[i] | ||
| + | s[i].tail = s[i] | ||
| + | s[i].next = null | ||
| − | + | '''int''' find('''SetItem''' x): <font color=green> // подразумевается, что <tex> x </tex> {{ --- }} ссылка на один из элементов </font> | |
| + | '''return''' x.head.data | ||
| − | + | '''func''' union('''SetItem''' x, '''SetItem''' y): <font color=green> // <tex> x </tex> и <tex> y </tex> {{ --- }} элементы множеств</font> | |
| + | x = x.head | ||
| + | y = y.head | ||
| + | '''if''' x == y | ||
| + | '''return''' | ||
| + | x.tail.next = y <font color=green> // соединим списки </font> | ||
| + | x.tail = y.tail <font color=green> // сделаем корректную ссылку на <tex> tail </tex> в <tex> head</tex></font> | ||
| + | '''while''' y <tex> \neq </tex> null <font color=green> // скорректируем ссылки на <tex> head </tex> у элементов множества <tex> y </tex> </font> | ||
| + | y.head = x | ||
| + | y = y.next | ||
| − | [[Файл: | + | [[Файл:DSU_list_example.png|800px|center|Пример объединения двух множеств (union)]] |
== Другие реализации == | == Другие реализации == | ||
| − | * [[СНМ(списки с весовой эвристикой)]] | + | * [[СНМ (списки с весовой эвристикой)]] |
| − | * [[СНМ(реализация с помощью леса корневых деревьев)]] | + | * [[СНМ (реализация с помощью леса корневых деревьев)]] |
| − | == Источники == | + | == Источники информации == |
| + | *[http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BD%D0%B5%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D0%BA%D0%B0%D1%8E%D1%89%D0%B8%D1%85%D1%81%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2 Википедия {{---}} Система непересекающихся множеств] | ||
| + | * [http://habrahabr.ru/blogs/algorithm/104772/ Система непересекающихся множеств и её применения] | ||
* Т. Кормен - Алгоритмы, построение и анализ. Второе издание. Часть V. Глава 21. | * Т. Кормен - Алгоритмы, построение и анализ. Второе издание. Часть V. Глава 21. | ||
| − | |||
| − | |||
| − | |||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:28, 4 сентября 2022
Система (лес, объединение) непересекающихся множеств (СНМ, disjoint set forest, DSF, disjoint set union, DSU) — иерархическая структура данных, позволяющая эффективно работать с множествами.
Содержание
Описание
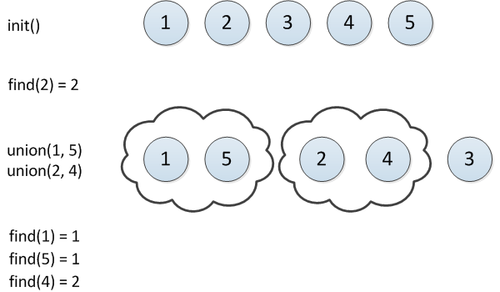
Структура хранит набор объектов (например, чисел от до ) в виде непересекающихся множеств. У каждого множества есть конкретный представитель.
Определены две операции:
- — объединяет множества, содержащие и
- — возвращает представителя множества, в котором находится
Для любого элемента множества представитель всегда одинаковый. Поэтому чтобы проверить принадлежность элементов и одному множеству достаточно сравнить и .
Реализации
С помощью массива
Пусть в массиве s хранятся номера множеств, в будет храниться номер множества, к которому принадлежит . Этот номер отождествляет множество, возвращает именно его. Тогда , очевидно, будет работать за .
Чтобы объединить множества и , надо изменить все , равные номеру множества , на номер . Тогда работает за .
int s[n]
func init():
for i = 0 to n - 1
s[i] = i // сначала каждый элемент лежит в своем множестве
int find(k):
return s[k]
func union(x, y):
if s[x] == s[y]
return
else
t = s[y]
for i = 0 to n - 1
if s[i] == t
s[i] = s[x]
С помощью списка
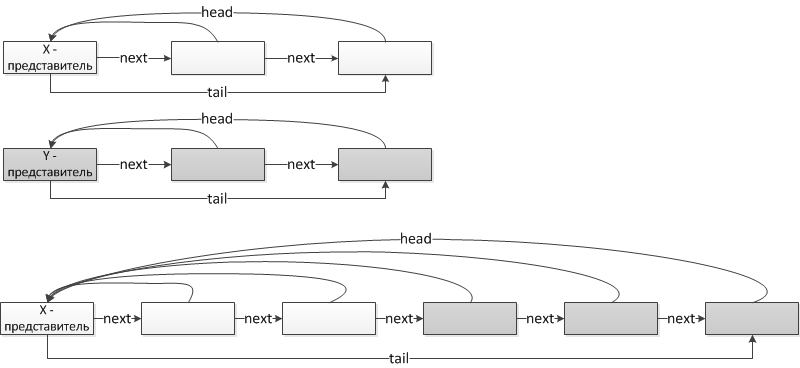
Будем хранить множество в виде списка. Для каждого элемента списка храним ссылку на следующий элемент и указатель на , который является представителем. Для того чтобы найти представителя, нужно перейти по ссылке на . Значит работает за .
Для объединения множеств потребуется объединить два списка и обновить ссылки на . Таким образом, работает за . Чтобы объединить два списка, нужно хранить ссылку на . Ее можно хранить в голове списка.
struct SetItem
int data
SetItem head
SetItem next
SetItem tail
SetItem s[n]
func init():
for i = 0 to n - 1
s[i].data = i
s[i].head = s[i]
s[i].tail = s[i]
s[i].next = null
int find(SetItem x): // подразумевается, что — ссылка на один из элементов
return x.head.data
func union(SetItem x, SetItem y): // и — элементы множеств x = x.head y = y.head if x == y return x.tail.next = y // соединим списки x.tail = y.tail // сделаем корректную ссылку на в while y null // скорректируем ссылки на у элементов множества y.head = x y = y.next
Другие реализации
Источники информации
- Википедия — Система непересекающихся множеств
- Система непересекающихся множеств и её применения
- Т. Кормен - Алгоритмы, построение и анализ. Второе издание. Часть V. Глава 21.