СНМ (списки с весовой эвристикой) — различия между версиями
(→Доказательство оценки времени выполнения) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 18 промежуточных версий 3 участников) | |||
| Строка 2: | Строка 2: | ||
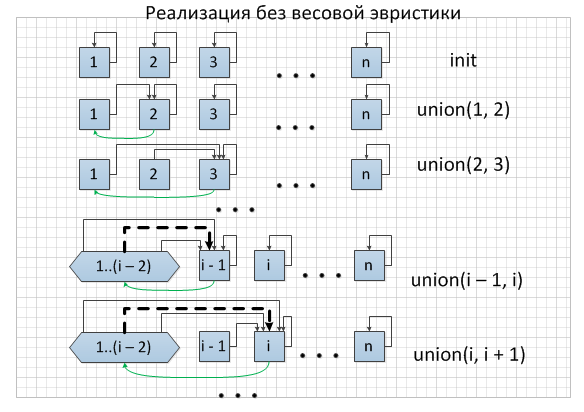
== Проблема наивной реализации == | == Проблема наивной реализации == | ||
| − | [[Файл:ve.png| | + | [[Файл:ve.png|right|600px|Оценка количества переподвешиваний]] |
Рассмотрим реализацию системы непересекающихся множеств с помощью списков. Для каждого элемента списка будем хранить указатель на представителя и на следующий элемент в списке. | Рассмотрим реализацию системы непересекающихся множеств с помощью списков. Для каждого элемента списка будем хранить указатель на представителя и на следующий элемент в списке. | ||
| − | При такой реализации операция init для создания n множеств из одного элемента займет <tex>O(n)</tex> времени. Для выполнения операции findSet достаточно перейти по ссылке на представителя за <tex>O(1)</tex>. Узким местом такой реализации является операция union. Слить списки и обновить указатели на представителя для одного из списков мы можем лишь за время пропорциональное количеству элементов. | + | При такой реализации операция <tex> \mathrm {init} </tex> для создания n множеств состоящих из одного элемента займет <tex>O(n)</tex> времени. Для выполнения операции <tex> \mathrm {findSet} </tex> достаточно перейти по ссылке на представителя за <tex>O(1)</tex>. Узким местом такой реализации является операция <tex> \mathrm {union} </tex>. Слить списки и обновить указатели на представителя для одного из списков мы можем лишь за время пропорциональное количеству элементов. |
| − | Нетрудно придумать последовательность из <tex>n - 1</tex> операций union, требующую <tex>O(n^2)</tex> времени. Достаточно каждый раз сливать одно и тоже множество с одним новым элементом в том порядке, чтобы требовалось обновить указатели на представителя именно элементам "большого" множества. Поскольку <tex>i</tex>-ая операция union обновляет <tex>i</tex> указателей, общее количество указателей, обновленных всеми <tex>n - 1</tex> операциями union равно <tex>\sum\limits_{i=1}^{n-1} i = O(n^2)</tex>. Отсюда следует, что амортизированное время выполнения операции union составляет <tex>O(n)</tex>. | + | Нетрудно придумать последовательность из <tex>n - 1</tex> операций <tex> \mathrm {union} </tex>, требующую <tex>O(n^2)</tex> времени. Достаточно каждый раз сливать одно и тоже множество с одним новым элементом в том порядке, чтобы требовалось обновить указатели на представителя именно элементам "большого" множества. Поскольку <tex>i</tex>-ая операция <tex> \mathrm {union} </tex> обновляет <tex>i</tex> указателей, общее количество указателей, обновленных всеми <tex>n - 1</tex> операциями <tex> \mathrm {union} </tex> равно <tex>\sum\limits_{i=1}^{n-1} i = O(n^2)</tex>. Отсюда следует, что амортизированное время выполнения операции <tex> \mathrm {union} </tex> составляет <tex>O(n)</tex>. |
== Реализация с весовой эвристикой == | == Реализация с весовой эвристикой == | ||
| − | Недостаток наивной реализации проявляется при слиянии относительно большого множества с множеством из одного элемента. В наивной реализации список указанный первым всегда подвешивается ко второму. Хотя в данном случае гораздо выгоднее подвесить меньший список к большему, обновив один указатель на представителя, вместо обновления большого числа указателей в первом списке. Отсюда следуют очевидная оптимизация {{ --- }} будем для каждого множества хранить его размер и изменять указатели на представителя всегда элементам из "меньшего" списка. Хотя одна операция union по-прежнему может потребовать <tex>\Omega(n)</tex> действий, если оба множества имеют <tex>\Omega(n)</tex> членов, но последовательность из <tex>n</tex> операций union требует <tex>O(n \log n)</tex> действий. | + | Недостаток наивной реализации проявляется при слиянии относительно большого множества с множеством из одного элемента. В наивной реализации список указанный первым всегда подвешивается ко второму. Хотя в данном случае гораздо выгоднее подвесить меньший список к большему, обновив один указатель на представителя, вместо обновления большого числа указателей в первом списке. Отсюда следуют очевидная оптимизация {{ --- }} будем для каждого множества хранить его размер и изменять указатели на представителя всегда элементам из "меньшего" списка. Хотя одна операция <tex> \mathrm {union} </tex> по-прежнему может потребовать <tex>\Omega(n)</tex> действий, если оба множества имеют <tex>\Omega(n)</tex> членов, но последовательность из <tex>n</tex> операций <tex> \mathrm {union} </tex> требует <tex>O(n \log n)</tex> действий. |
'''Псевдокод:''' | '''Псевдокод:''' | ||
s[n] | s[n] | ||
| − | init(): | + | '''function''' init(): |
| − | + | '''for''' i = 0 '''to''' n - 1 | |
| − | + | s[i].set = i <font color = "green">// номер-идентификатор множества</font> | |
| − | + | s[i].next = null | |
| − | + | s[i].head = s[i] | |
| − | + | s[i].tail = s[i] <font color = "green">// храним только для представителя</font> | |
| − | + | s[i].count = 1 <font color = "green">// храним только для представителя</font> | |
| − | find(x): // подразумевается, что x {{ --- }} ссылка на один из элементов | + | '''T''' find(x): <font color = "green">// подразумевается, что x {{ --- }} ссылка на один из элементов</font> |
| − | + | '''return''' x.head.set | |
| − | union(x, y): | + | '''function''' union(x, y): |
| − | + | x = x.head | |
| − | + | y = y.head | |
| − | + | '''if''' x == y | |
| − | + | '''return''' | |
| − | + | '''else''' | |
| − | + | '''if''' x.count > y.count | |
| − | + | swap(x, y) | |
| − | + | i = x.head | |
| − | + | '''while''' i != null | |
| − | + | i.head = y | |
| − | + | i = i.next | |
| − | + | y.tail.next = x.head <font color = "green">// соединили списки</font> | |
| − | + | y.tail = x.tail | |
| − | + | y.count += x.count | |
== Доказательство оценки времени выполнения == | == Доказательство оценки времени выполнения == | ||
{{Утверждение | {{Утверждение | ||
| − | |statement=При реализации СНМ на списках с указателями на представителя и применении весовой эвристики, последовательность из операции init для n элементов и m операций union и findSet, требует для выполнения <tex>O(m+n \log n)</tex> действий. | + | |statement=При реализации СНМ на списках с указателями на представителя и применении весовой эвристики, последовательность из операции <tex> \mathrm {init} </tex> для n элементов и m операций <tex> \mathrm {union} </tex> и <tex> \mathrm {findSet} </tex>, требует для выполнения <tex>O(m+n \log n)</tex> действий. |
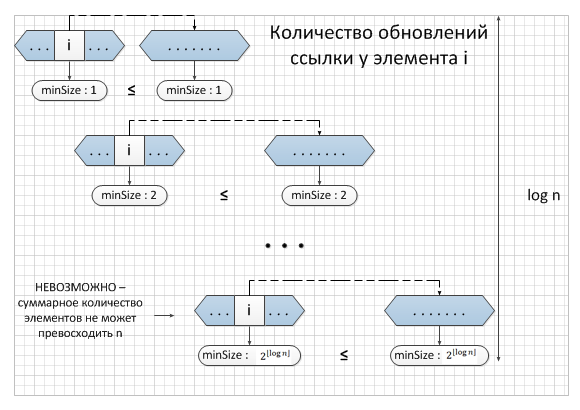
| − | |proof = [[Файл:ve2.png| | + | |proof = [[Файл:ve2.png|right|600px|Оценка количества переподвешиваний]] Оценим время работы необходимое для обновления указателей на представителя в операциях <tex> \mathrm {union} </tex>. Рассмотрим количество обновлений отдельно для каждого элемента. |
| − | Оказывается, что для каждого элемента мы можем обновить указатель не более <tex>O(\log n)</tex> раз. Это связано с тем, что при каждом объединении множество в котором оказывается объект увеличивается не менее чем вдвое. Действительно, так как мы обновляем указатель на представителя элементу, то этот элемент находился в меньшем из множеств (согласно нашей эвристике), но тогда размер второго множества не меньше. Тогда после первого обновления элемент содержится в множестве в котором не менее двух элементов, после второго {{ --- }} четырех, и так далее. В силу того, что множество не может содержать более n элементов, количество обновлений не превосходит <tex>O(\log n)</tex>. | + | Оказывается, что для каждого элемента мы можем обновить указатель не более <tex>O(\log n)</tex> раз. Это связано с тем, что при каждом объединении, множество, в котором оказывается объект, увеличивается не менее чем вдвое. Действительно, так как мы обновляем указатель на представителя элементу, то этот элемент находился в меньшем из множеств (согласно нашей эвристике), но тогда размер второго множества не меньше. Тогда после первого обновления элемент содержится в множестве, в котором не менее двух элементов, после второго {{ --- }} четырех, и так далее. В силу того, что множество не может содержать более n элементов, количество обновлений не превосходит <tex>O(\log n)</tex>. |
Таким образом, общее время, необходимое для обновления указателей для n элементов, составляет <tex>O(n \log n)</tex>. | Таким образом, общее время, необходимое для обновления указателей для n элементов, составляет <tex>O(n \log n)</tex>. | ||
| − | Необходимо также отметить, что слить два списка и обновить поле длины при выполнении | + | Необходимо также отметить, что слить два списка и обновить поле длины при выполнении <tex> \mathrm {union} </tex> можно за константное количество операций (последние три строчки в псевдокоде). |
| − | Отсюда легко понять, что время необходимое для выполнения всей последовательности | + | Отсюда легко понять, что время необходимое для выполнения всей последовательности операций составит <tex>O(m + n \log n)</tex>. Операция <tex> \mathrm {init} </tex> за <tex>O(n)</tex>, <tex>O(m)</tex> операций <tex> \mathrm {findSet} </tex> и часть работы операции <tex> \mathrm {union} </tex> на обновление поля длины и слияния списков, каждая из которых выполняется за константное время, а также суммарное время обновления указателей на представителя операцией <tex> \mathrm {union} </tex> для каждого элемента за <tex>O(n \log n)</tex> действий. |
}} | }} | ||
| Строка 60: | Строка 60: | ||
* [[СНМ(наивные реализации)]] | * [[СНМ(наивные реализации)]] | ||
* [[СНМ(реализация с помощью леса корневых деревьев)]] | * [[СНМ(реализация с помощью леса корневых деревьев)]] | ||
| − | |||
| − | |||
| − | |||
== Ссылки == | == Ссылки == | ||
* [http://habrahabr.ru/blogs/algorithm/104772/ habrahabr.ru - Система непересекающихся множеств и её применения] | * [http://habrahabr.ru/blogs/algorithm/104772/ habrahabr.ru - Система непересекающихся множеств и её применения] | ||
| + | * Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 585—588. — ISBN 5-8489-0857-4 | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
Текущая версия на 19:38, 4 сентября 2022
Весовая эвристика (weighted-union heuristic) — улучшение наивной реализации СНМ на списках с указателями на представителя. Позволяет добиться улучшения асимптотики с до благодаря добавлению меньшего списка к большему при объединении множеств.
Содержание
Проблема наивной реализации
Рассмотрим реализацию системы непересекающихся множеств с помощью списков. Для каждого элемента списка будем хранить указатель на представителя и на следующий элемент в списке.
При такой реализации операция для создания n множеств состоящих из одного элемента займет времени. Для выполнения операции достаточно перейти по ссылке на представителя за . Узким местом такой реализации является операция . Слить списки и обновить указатели на представителя для одного из списков мы можем лишь за время пропорциональное количеству элементов.
Нетрудно придумать последовательность из операций , требующую времени. Достаточно каждый раз сливать одно и тоже множество с одним новым элементом в том порядке, чтобы требовалось обновить указатели на представителя именно элементам "большого" множества. Поскольку -ая операция обновляет указателей, общее количество указателей, обновленных всеми операциями равно . Отсюда следует, что амортизированное время выполнения операции составляет .
Реализация с весовой эвристикой
Недостаток наивной реализации проявляется при слиянии относительно большого множества с множеством из одного элемента. В наивной реализации список указанный первым всегда подвешивается ко второму. Хотя в данном случае гораздо выгоднее подвесить меньший список к большему, обновив один указатель на представителя, вместо обновления большого числа указателей в первом списке. Отсюда следуют очевидная оптимизация — будем для каждого множества хранить его размер и изменять указатели на представителя всегда элементам из "меньшего" списка. Хотя одна операция по-прежнему может потребовать действий, если оба множества имеют членов, но последовательность из операций требует действий.
Псевдокод:
s[n]
function init():
for i = 0 to n - 1
s[i].set = i // номер-идентификатор множества
s[i].next = null
s[i].head = s[i]
s[i].tail = s[i] // храним только для представителя
s[i].count = 1 // храним только для представителя
T find(x): // подразумевается, что x — ссылка на один из элементов
return x.head.set
function union(x, y):
x = x.head
y = y.head
if x == y
return
else
if x.count > y.count
swap(x, y)
i = x.head
while i != null
i.head = y
i = i.next
y.tail.next = x.head // соединили списки
y.tail = x.tail
y.count += x.count
Доказательство оценки времени выполнения
| Утверждение: |
При реализации СНМ на списках с указателями на представителя и применении весовой эвристики, последовательность из операции для n элементов и m операций и , требует для выполнения действий. |
|
Оценим время работы необходимое для обновления указателей на представителя в операциях . Рассмотрим количество обновлений отдельно для каждого элемента.
Оказывается, что для каждого элемента мы можем обновить указатель не более раз. Это связано с тем, что при каждом объединении, множество, в котором оказывается объект, увеличивается не менее чем вдвое. Действительно, так как мы обновляем указатель на представителя элементу, то этот элемент находился в меньшем из множеств (согласно нашей эвристике), но тогда размер второго множества не меньше. Тогда после первого обновления элемент содержится в множестве, в котором не менее двух элементов, после второго — четырех, и так далее. В силу того, что множество не может содержать более n элементов, количество обновлений не превосходит . Таким образом, общее время, необходимое для обновления указателей для n элементов, составляет . Необходимо также отметить, что слить два списка и обновить поле длины при выполнении можно за константное количество операций (последние три строчки в псевдокоде). Отсюда легко понять, что время необходимое для выполнения всей последовательности операций составит . Операция за , операций и часть работы операции на обновление поля длины и слияния списков, каждая из которых выполняется за константное время, а также суммарное время обновления указателей на представителя операцией для каждого элемента за действий. |
Другие реализации
Ссылки
- habrahabr.ru - Система непересекающихся множеств и её применения
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 585—588. — ISBN 5-8489-0857-4