Левосторонняя куча — различия между версиями
(→merge) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 26 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
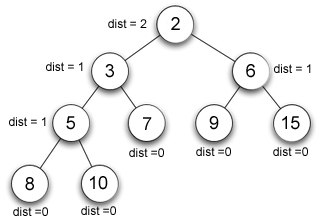
| − | == | + | [[Файл:LeftistHeap.jpg|400px|thumb|right|Левосторонняя куча]] |
| + | ==Условие кучи== | ||
Левосторонние деревья были изобретены Кларком Крейном (Clark Allan Crane), свое название они получили из-за того, что левое поддерево обычно длиннее правого. | Левосторонние деревья были изобретены Кларком Крейном (Clark Allan Crane), свое название они получили из-за того, что левое поддерево обычно длиннее правого. | ||
{{Определение | {{Определение | ||
| − | |definition='''Левосторонняя куча (leftist heap | + | |definition='''Левосторонняя куча''' (англ. ''leftist heap'') {{---}} двоичное левосторонее [[Дерево, эквивалентные определения|дерево]] (не обязательно сбалансированное), но с соблюдением [[Двоичная куча#Определение|порядка кучи]] (heap order).}} |
| + | '''Свободной позицией''' назовем место в дереве, куда может быть вставлена новая вершина. Само дерево будет являться свободной позицией, если оно не содержит вершин. Если же у какой-то внутренней вершины нет сына, то на его месте {{---}} ''свободная позиция''. | ||
{{Лемма | {{Лемма | ||
|id=lemma1 | |id=lemma1 | ||
| Строка 10: | Строка 12: | ||
Левосторонняя куча накладывает на двоичное дерево дополнительное условие. | Левосторонняя куча накладывает на двоичное дерево дополнительное условие. | ||
| − | Ближайшая свободная позиция должна быть самой правой позицией в дереве. То есть помимо условия кучи выполняется следующее: | + | Ближайшая свободная позиция должна быть самой правой позицией в дереве. То есть помимо обычного условия кучи выполняется следующее: |
{{Определение | {{Определение | ||
| − | |definition=Условие левосторонней кучи. Пусть <tex>dist(u)</tex> | + | |definition='''Условие левосторонней кучи'''. Пусть <tex>dist(u)</tex> {{---}} расстояние от вершины <tex>u</tex> до ближайшей свободной позиции в ее поддереве. У пустых позиций <tex>dist = 0</tex>. Тогда потребуем для любой вершины <tex>u : dist(u.left)\geqslant dist(u.right)</tex>.}} |
Если для какой- то вершины это свойство не выполняется, то это легко устраняется: можно за <tex>O(1)</tex> поменять местами левого и правого ребенка, что не повлияет на порядок кучи. | Если для какой- то вершины это свойство не выполняется, то это легко устраняется: можно за <tex>O(1)</tex> поменять местами левого и правого ребенка, что не повлияет на порядок кучи. | ||
| Строка 20: | Строка 22: | ||
===merge=== | ===merge=== | ||
Слияние двух куч. | Слияние двух куч. | ||
| − | + | ||
| − | if x == | + | '''LeftistHeap''' merge(x, y): <font color=darkgreen>// x, y {{---}} корни двух деревьев</font> |
| − | if y == | + | '''if''' x == <tex> \varnothing </tex>: |
| − | if y.key < x.key : | + | '''return''' y |
| − | + | '''if''' y == <tex> \varnothing </tex>: | |
| − | //Воспользуемся тем, что куча левосторонняя. Правая ветка | + | '''return''' x |
| − | // | + | '''if''' y.key < x.key: |
| − | x. | + | swap(x, y) |
| − | //Могло возникнуть нарушение левостороннести кучи | + | <font color=darkgreen>// Воспользуемся тем, что куча левосторонняя. Правая ветка {{---}} самая короткая и не длиннее логарифма. |
| − | + | // Пойдем направо и сольем правое поддерево с у.</font> | |
| − | + | x.right = '''merge'''(x.right, y) | |
| − | + | <font color=darkgreen>// Могло возникнуть нарушение левостороннести кучи</font> | |
| − | return x | + | '''if''' dist(x.right) > dist(x.left): |
| − | //Каждый раз | + | swap(x.left, x.right) |
| + | dist(x) = dist(x.right) + 1 <font color=darkgreen>// пересчитаем расстояние до ближайшей свободной позиции</font> | ||
| + | '''return''' x | ||
| + | <font color=darkgreen>// Каждый раз идем из уже существующей вершины только в правое поддерево {{---}} не более логарифма вызовов (по лемме)</font> | ||
Левосторонняя куча относится к сливаемым кучам: остальные операции легко реализуются с помощью операции слияния. | Левосторонняя куча относится к сливаемым кучам: остальные операции легко реализуются с помощью операции слияния. | ||
| Строка 42: | Строка 47: | ||
Как и у любой другой двоичной кучи, минимум хранится в корне. Извлекаем минимальное значение, удаляем корень, сливаем левое и правое поддерево корня. Возвращает пару из извлеченной вершины и новой кучи. | Как и у любой другой двоичной кучи, минимум хранится в корне. Извлекаем минимальное значение, удаляем корень, сливаем левое и правое поддерево корня. Возвращает пару из извлеченной вершины и новой кучи. | ||
===delete=== | ===delete=== | ||
| − | Аналогично удаляется любой элемент | + | Аналогично удаляется любой элемент {{---}} на его место ставится результат слияния его детей. Но так просто любой элемент удалить нельзя {{---}} на пути от этого элемента к корню может нарушиться левостороннесть кучи. А до корня мы дойти не можем, так как элемент может находиться на линейной глубине. Поэтому удаление реализуется с помощью <tex>\mathrm{decreaseKey}</tex>. Уменьшаем ключ до <tex>-\infty</tex>, затем извлекаем минимальное значение. |
| − | === | + | ===decreaseKey=== |
{{Лемма | {{Лемма | ||
|id=lemma2 | |id=lemma2 | ||
|about=2 | |about=2 | ||
| − | |statement=У левостороннего дерева с правой ветвью | + | |statement=У левостороннего дерева с правой ветвью длины <tex>h</tex> количество узлов <tex>n \geqslant 2^{h} - 1</tex>. |
|proof=Индукция по h. | |proof=Индукция по h. | ||
| − | При <tex>h = 1</tex> | + | При <tex>h = 1</tex> {{---}} верно. |
При <tex>h > 1</tex> левое и правое поддеревья исходного дерева левосторонние, а <tex>dist</tex> от их корней больше либо равен <tex>h - 1</tex>. | При <tex>h > 1</tex> левое и правое поддеревья исходного дерева левосторонние, а <tex>dist</tex> от их корней больше либо равен <tex>h - 1</tex>. | ||
| − | По индукции число узлов в каждом из них больше или равно <tex>2^{h - 1} - 1</tex>, тогда во | + | По индукции число узлов в каждом из них больше или равно <tex>2^{h - 1} - 1</tex>, тогда во всем дереве <tex>n \geqslant (2^{h - 1} - 1) + (2^{h - 1} - 1) + 1 = 2^{h} - 1</tex> узлов.}} |
====Алгоритм==== | ====Алгоритм==== | ||
| − | + | * Найдем узел <tex>x</tex>, вырежем поддерево с корнем в этом узле. | |
| − | + | * Пройдем от предка вырезанной вершины, при этом пересчитывая <tex>dist</tex>. Если <tex>dist</tex> левого сына вершины меньше <tex>dist</tex> правого, то меняем местами поддеревья. | |
| − | + | * Уменьшаем ключ данного узла и сливаем два дерева: исходное и вырезанное. | |
| − | |||
{{Лемма | {{Лемма | ||
|id=lemma3 | |id=lemma3 | ||
|about=3 | |about=3 | ||
|statement= Нужно транспонировать не более <tex>\log{n}</tex> поддеревьев. | |statement= Нужно транспонировать не более <tex>\log{n}</tex> поддеревьев. | ||
| − | |proof=Длина пути от вершины до корня может быть и <tex>O(n)</tex>, но нам не нужно подниматься до корня | + | |proof=Длина пути от вершины до корня может быть и <tex>O(n)</tex>, но нам не нужно подниматься до корня {{---}} достаточно подняться до вершины, у которой свойство левосторонней кучи уже выполнено. Транспонируем только если <tex>dist(x.left) < dist(x.right)</tex>, но <tex>dist(x.right) \leqslant \log{n}</tex>. На каждом шаге, если нужно транспонируем и увеличиваем <tex>dist</tex>, тогда <tex>dist</tex> увеличится до <tex>\log{n}</tex> и обменов уже не надо будет делать.}} |
| − | Таким образом, мы восстановили левостороннесть кучи за <tex>O(\log{n})</tex>. | + | Таким образом, мы восстановили левостороннесть кучи за <tex>O(\log{n})</tex>. Поэтому асимптотика операции <tex>\mathrm{decreaseKey} </tex> {{---}} <tex>O(\log{n})</tex>. |
| + | |||
| + | ==Построение кучи за O(n)== | ||
| + | Храним список левосторонних куч. Пока их количество больше <tex>1</tex>, из начала списка достаем две кучи, сливаем их и кладем в конец списка. | ||
| + | |||
| + | Покажем, почему это будет работать за <tex> O(n) </tex>. | ||
| + | |||
| + | Пусть на <tex> i </tex>-ом шаге алгоритма в нашем списке остались только кучи размера <tex> 2^i </tex>. На нулевом шаге у нас <tex> n </tex> куч из одного элемента, и на каждом следующем количество куч будет уменьшаться вдвое, а число вершин в куче будет увеличиваться вдвое. Слияние двух куч из <tex> n_i </tex> элементов выполняется за <tex> O(\log{n_i}) </tex>. Поэтому построение будет выполняться за | ||
| + | |||
| + | <tex > | ||
| + | \sum\limits_{i = 1}^{\left\lceil \log{n} \right\rceil} \dfrac{n \cdot \log{n_i}}{2^i} = | ||
| + | n \cdot \sum\limits_{i = 1}^{\left\lceil \log{n} \right\rceil} \dfrac{\log{2^i}}{2^i} = | ||
| + | n \cdot \sum\limits_{i = 1}^{\left\lceil \log{n} \right\rceil} \dfrac{i}{2^i} | ||
| + | </tex> | ||
| + | |||
| + | Покажем, что сумма {{---}} <tex> O(1) </tex>, тогда и алгоритм будет выполняться за <tex> O(n) </tex>. Найдём сумму [[Определение суммы числового ряда|ряда]], заменив его на эквивалентный [[Определение функционального ряда|функциональный]]: | ||
| + | |||
| + | <tex> | ||
| + | \sum\limits_{i = 1}^{\left\lceil \log{n} \right\rceil} \dfrac{i}{2^i} < \sum\limits_{i = 1}^{\infty } \dfrac{i}{2^i} \\ | ||
| + | f(x) = \sum\limits_{i = 1}^{\infty } \Bigl. i \cdot x^i \Bigr|_{x = \frac{1}{2}} \\ | ||
| + | ~\dfrac{f(x)}{x} = \sum\limits_{i = 1}^{\infty } i \cdot x^{i - 1} = \sum\limits_{i = 1}^{\infty } (x^i)' = \left(\sum\limits_{i = 1}^{\infty } x^i \right)' \\ | ||
| + | ~\int\dfrac{f(x)}{x} = \sum\limits_{i = 1}^{\infty } x^i =~\dfrac{1}{1 - x} - 1 \\ | ||
| + | ~\dfrac{f(x)}{x} = \left(\dfrac{1}{1 - x} - 1\right)' = \dfrac{1}{(1 - x)^2} \\ | ||
| + | ~f(x) = \dfrac{x}{(1 - x)^2} | ||
| + | </tex> | ||
| + | |||
| + | После подстановки <tex> x = \dfrac{1}{2} </tex> получаем, что сумма равна <tex> 2 </tex>. Следовательно, построение кучи таким образом произойдёт за <tex> O(n) </tex>. | ||
| − | |||
| − | |||
| − | |||
==Преимущества левосторонней кучи== | ==Преимущества левосторонней кучи== | ||
| − | Нигде не делается уничтожающих присваиваний. Не создается новых узлов в <tex>merge</tex>. Эта реализация слияния является функциональной — ее легко реализовать на функциональном языке программирования. Также данная | + | Нигде не делается уничтожающих присваиваний. Не создается новых узлов в <tex>\mathrm{merge}</tex>. Эта реализация слияния является функциональной — ее легко реализовать на функциональном языке программирования. Также данная реализация <tex>\mathrm{merge}</tex> является персистентной. |
| + | |||
| + | ==Источники информации== | ||
| + | * [http://compscicenter.ru/program/lecture/6829 Лекция "Приоритетные очереди" А. С. Станкевича в Computer Science Center] | ||
| + | * [http://www.intuit.ru/studies/courses/100/100/lecture/1539?page=1 Левосторонние кучи. Интуит.] | ||
| + | * [[wikipedia:Leftist_tree|Wikipedia {{---}} Leftist tree]] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Приоритетные очереди]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:05, 4 сентября 2022
Содержание
Условие кучи
Левосторонние деревья были изобретены Кларком Крейном (Clark Allan Crane), свое название они получили из-за того, что левое поддерево обычно длиннее правого.
| Определение: |
| Левосторонняя куча (англ. leftist heap) — двоичное левосторонее дерево (не обязательно сбалансированное), но с соблюдением порядка кучи (heap order). |
Свободной позицией назовем место в дереве, куда может быть вставлена новая вершина. Само дерево будет являться свободной позицией, если оно не содержит вершин. Если же у какой-то внутренней вершины нет сына, то на его месте — свободная позиция.
| Лемма (1): |
В двоичном дереве с вершинами существует свободная позиция на глубине не более . |
| Доказательство: |
| Если бы все свободные позиции были на глубине более логарифма, то мы получили бы полное дерево с количеством вершин более . |
Левосторонняя куча накладывает на двоичное дерево дополнительное условие. Ближайшая свободная позиция должна быть самой правой позицией в дереве. То есть помимо обычного условия кучи выполняется следующее:
| Определение: |
| Условие левосторонней кучи. Пусть — расстояние от вершины до ближайшей свободной позиции в ее поддереве. У пустых позиций . Тогда потребуем для любой вершины . |
Если для какой- то вершины это свойство не выполняется, то это легко устраняется: можно за поменять местами левого и правого ребенка, что не повлияет на порядок кучи.
Поддерживаемые операции
merge
Слияние двух куч.
LeftistHeap merge(x, y): // x, y — корни двух деревьев if x == : return y if y == : return x if y.key < x.key: swap(x, y) // Воспользуемся тем, что куча левосторонняя. Правая ветка — самая короткая и не длиннее логарифма. // Пойдем направо и сольем правое поддерево с у. x.right = merge(x.right, y) // Могло возникнуть нарушение левостороннести кучи if dist(x.right) > dist(x.left): swap(x.left, x.right) dist(x) = dist(x.right) + 1 // пересчитаем расстояние до ближайшей свободной позиции return x // Каждый раз идем из уже существующей вершины только в правое поддерево — не более логарифма вызовов (по лемме)
Левосторонняя куча относится к сливаемым кучам: остальные операции легко реализуются с помощью операции слияния.
insert
Вставка новой вершины в дерево. Новое левостороннее дерево, состоящее из одной вершины, сливается с исходным.
extractMin
Как и у любой другой двоичной кучи, минимум хранится в корне. Извлекаем минимальное значение, удаляем корень, сливаем левое и правое поддерево корня. Возвращает пару из извлеченной вершины и новой кучи.
delete
Аналогично удаляется любой элемент — на его место ставится результат слияния его детей. Но так просто любой элемент удалить нельзя — на пути от этого элемента к корню может нарушиться левостороннесть кучи. А до корня мы дойти не можем, так как элемент может находиться на линейной глубине. Поэтому удаление реализуется с помощью . Уменьшаем ключ до , затем извлекаем минимальное значение.
decreaseKey
| Лемма (2): |
У левостороннего дерева с правой ветвью длины количество узлов . |
| Доказательство: |
|
Индукция по h. При — верно. При левое и правое поддеревья исходного дерева левосторонние, а от их корней больше либо равен . По индукции число узлов в каждом из них больше или равно , тогда во всем дереве узлов. |
Алгоритм
- Найдем узел , вырежем поддерево с корнем в этом узле.
- Пройдем от предка вырезанной вершины, при этом пересчитывая . Если левого сына вершины меньше правого, то меняем местами поддеревья.
- Уменьшаем ключ данного узла и сливаем два дерева: исходное и вырезанное.
| Лемма (3): |
Нужно транспонировать не более поддеревьев. |
| Доказательство: |
| Длина пути от вершины до корня может быть и , но нам не нужно подниматься до корня — достаточно подняться до вершины, у которой свойство левосторонней кучи уже выполнено. Транспонируем только если , но . На каждом шаге, если нужно транспонируем и увеличиваем , тогда увеличится до и обменов уже не надо будет делать. |
Таким образом, мы восстановили левостороннесть кучи за . Поэтому асимптотика операции — .
Построение кучи за O(n)
Храним список левосторонних куч. Пока их количество больше , из начала списка достаем две кучи, сливаем их и кладем в конец списка.
Покажем, почему это будет работать за .
Пусть на -ом шаге алгоритма в нашем списке остались только кучи размера . На нулевом шаге у нас куч из одного элемента, и на каждом следующем количество куч будет уменьшаться вдвое, а число вершин в куче будет увеличиваться вдвое. Слияние двух куч из элементов выполняется за . Поэтому построение будет выполняться за
Покажем, что сумма — , тогда и алгоритм будет выполняться за . Найдём сумму ряда, заменив его на эквивалентный функциональный:
После подстановки получаем, что сумма равна . Следовательно, построение кучи таким образом произойдёт за .
Преимущества левосторонней кучи
Нигде не делается уничтожающих присваиваний. Не создается новых узлов в . Эта реализация слияния является функциональной — ее легко реализовать на функциональном языке программирования. Также данная реализация является персистентной.