Замкнутость КС-языков относительно различных операций — различия между версиями
Igorjan94 (обсуждение | вклад) (→Прямой и обратный гомоморфизм) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 50 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
В отличие от [[Замкнутость регулярных языков относительно различных операций|регулярных языков]], [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|КС-языки]] не замкнуты относительно всех теоретико-множественных операций. К примеру, дополнение и пересечение КС-языков не обязательно являются КС-языками. | В отличие от [[Замкнутость регулярных языков относительно различных операций|регулярных языков]], [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|КС-языки]] не замкнуты относительно всех теоретико-множественных операций. К примеру, дополнение и пересечение КС-языков не обязательно являются КС-языками. | ||
| − | Здесь и далее считаем, что <tex> L_1 </tex> и <tex> L_2 </tex> — КС языки. | + | Здесь и далее считаем, что <tex> L_1 </tex> и <tex> L_2 </tex> — КС-языки. |
== Операции с КС-языками == | == Операции с КС-языками == | ||
| Строка 8: | Строка 8: | ||
{{ Утверждение | {{ Утверждение | ||
| − | |statement= <tex> L_1 \cup L_2 </tex> | + | |statement= <tex> L_1 \cup L_2 </tex> является КС-языком. |
|proof= | |proof= | ||
| − | Построим [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|КС-грамматику]] для языка <tex> L_1 \cup L_2 </tex>. Для этого рассмотрим соответствующие КС-грамматики для языков <tex> L_1 </tex> и <tex> L_2 </tex>. Пусть стартовые символы в них имеют имена <tex> S </tex> и <tex> T </tex> соответственно. Тогда стартовый символ для <tex> L_1 \cup L_2 </tex> обозначим за <tex> S' </tex> и добавим правило <tex> S' \to S\ | + | Построим [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|КС-грамматику]] для языка <tex> L_1 \cup L_2 </tex>. Для этого рассмотрим соответствующие КС-грамматики для языков <tex> L_1 </tex> и <tex> L_2 </tex>. Пусть стартовые символы в них имеют имена <tex> S </tex> и <tex> T </tex> соответственно. Тогда стартовый символ для <tex> L_1 \cup L_2 </tex> обозначим за <tex> S' </tex> и добавим правило <tex> S' \to S \mid T </tex>. |
| − | Покажем, что <tex> S' \Rightarrow^{*} w \iff S \Rightarrow^{*} w \lor T \Rightarrow^{*} w | + | Покажем, что <tex> S' \Rightarrow^{*} w \iff S \Rightarrow^{*} w \lor T \Rightarrow^{*} w </tex>. |
| − | + | <tex>\Rightarrow</tex> | |
| + | : Поскольку <tex> S \Rightarrow^{*} w </tex> и есть правило <tex> S' \to S </tex>, то, по определению <tex> \Rightarrow^{*} </tex> получаем, что <tex> S' \Rightarrow^{*} w </tex>. Аналогично и для <tex> T </tex>. | ||
| + | |||
| + | <tex>\Leftarrow </tex> | ||
| + | : Пусть <tex> S' \Rightarrow^{*} w </tex>. Поскольку <tex> S' \to S \mid T </tex> — единственные правила, в которых нетерминал <tex> S' </tex> присутствует в правой части, то это означает, что либо <tex> S' \Rightarrow S \Rightarrow^{*} w </tex>, либо <tex> S' \Rightarrow T \Rightarrow^{*} w </tex>. | ||
}} | }} | ||
| Строка 22: | Строка 26: | ||
{{ Утверждение | {{ Утверждение | ||
| − | |statement= <tex> L_1 | + | |statement= <tex> L_1 L_2 </tex> — КС-язык. |
| − | |proof=Аналогично предыдущему случаю построим КС-грамматику для языка <tex> L_1 | + | |proof=Аналогично предыдущему случаю построим КС-грамматику для языка <tex> L_1 L_2 </tex>. Для этого добавим правило <tex> S' \to S T </tex>, где <tex> S </tex> и <tex> T </tex> — стартовые символы языков <tex> L_1 </tex> и <tex> L_2 </tex> соответственно. |
| − | |||
}} | }} | ||
| − | === Замыкание Клини === | + | === [[Основные определения, связанные со строками#Формальные языки | Замыкание Клини]] === |
{{ Утверждение | {{ Утверждение | ||
|statement= <tex> L^{*} = \bigcup\limits_{i = 0}^{\infty} L^i </tex> — КС-язык. | |statement= <tex> L^{*} = \bigcup\limits_{i = 0}^{\infty} L^i </tex> — КС-язык. | ||
| − | |proof=Если <tex> S </tex> — стартовый символ КС-грамматики для языка <tex> L </tex>, то добавим в КС-грамматику для языка <tex> L^{*} </tex> новый стартовый символ <tex> S' </tex> и правила <tex> S' \to S S' \ | + | |proof=Если <tex> S </tex> — стартовый символ КС-грамматики для языка <tex> L </tex>, то добавим в КС-грамматику для языка <tex> L^{*} </tex> новый стартовый символ <tex> S' </tex> и правила <tex> S' \to S S' \mid \varepsilon </tex>. |
}} | }} | ||
| − | === Прямой | + | ===Гомоморфизмы === |
| + | ==== [[Основные определения, связанные со строками#Гомоморфизм языков | Прямой гомоморфизм]] ==== | ||
| − | + | {{ Утверждение | |
| + | |statement= КС-языки замкнуты относительно прямого гомоморфизма. | ||
| + | |proof= | ||
| + | Построим КС-грамматику, в которой каждый символ <tex> x \in \Sigma </tex> заменим на <tex> \mathrm{h}(x) </tex>. | ||
| + | }} | ||
| − | + | ==== [[Основные определения, связанные со строками#Гомоморфизм языков | Обратный гомоморфизм]] ==== | |
| + | {{ Утверждение | ||
| + | |statement= КС-языки замкнуты относительно обратного гомоморфизма. | ||
| + | |proof= | ||
| + | [[Файл:Homo.png|300px|right|frameless]] | ||
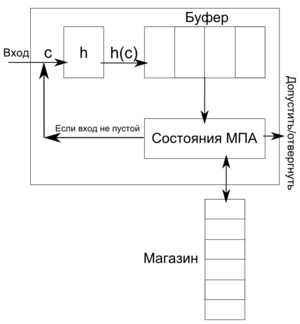
| + | Докажем аналогично соответствующему утверждению для регулярных языков. Построим [[Автоматы с магазинной памятью|МП-автомат]] для <tex> \mathrm{h^{-1}}(L) = \{ w \mid \mathrm{h}(w) \in L \} </tex> на основе МП-автомата для языка <tex> L </tex> (назовем его <tex> M </tex>). Новый автомат <tex> M' </tex> будет действовать следующим образом: | ||
| − | # Если входное слово закончилось, допускаем или не допускаем его по пустому стеку. | + | # Если входное слово закончилось, допускаем или не допускаем его [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность|по допускающему состоянию]]. |
| − | # | + | # Считываем символ <tex> c </tex>. |
| − | # Сохраняем <tex> h(c) </tex> в буфере. | + | # Сохраняем <tex> \mathrm{h}(c) </tex> в буфере (входная лента для автомата <tex> M </tex>). |
# Запускаем <tex> M </tex> на слове, находящемся в буфере. | # Запускаем <tex> M </tex> на слове, находящемся в буфере. | ||
| − | # После того, как <tex> M </tex> обработал весь буфер, переходим к пункту | + | # После того, как <tex> M </tex> обработал весь буфер, переходим к пункту 1. |
Если рассмотреть более формально, пусть <tex> M =\langle Q, \Sigma, \Gamma, \delta, s, Z_{0}, T\rangle </tex>, тогда <tex> M' =\langle Q', \Sigma, \Gamma, \delta', (s, \varepsilon), Z_{0}, T \times {\varepsilon}\rangle</tex>. | Если рассмотреть более формально, пусть <tex> M =\langle Q, \Sigma, \Gamma, \delta, s, Z_{0}, T\rangle </tex>, тогда <tex> M' =\langle Q', \Sigma, \Gamma, \delta', (s, \varepsilon), Z_{0}, T \times {\varepsilon}\rangle</tex>. | ||
* <tex> Q' = \{ (q, x) \mid q \in Q \} </tex>, где <tex> x </tex> — суффикс (не обязательно собственный) некоторой цепочки <tex> h(c) </tex> для символа <tex> c \in \Sigma </tex>. Таким образом, первый компонент состояния <tex> M' </tex> является состоянием <tex> M </tex>, а второй — компонентом буфера. | * <tex> Q' = \{ (q, x) \mid q \in Q \} </tex>, где <tex> x </tex> — суффикс (не обязательно собственный) некоторой цепочки <tex> h(c) </tex> для символа <tex> c \in \Sigma </tex>. Таким образом, первый компонент состояния <tex> M' </tex> является состоянием <tex> M </tex>, а второй — компонентом буфера. | ||
* <tex> \delta' </tex> определяется следующими правилами: | * <tex> \delta' </tex> определяется следующими правилами: | ||
| − | ** <tex> \delta'((q, \varepsilon), c, X) = \{((q, h(c)), X) \mid c \in \Sigma, q \in Q, X \in \Gamma \}</tex>. Когда буфер пуст, <tex> M' </tex> может прочитать свой следующий входной символ <tex> c </tex> и поместить <tex> h(c) </tex> в буфер. | + | ** <tex> \delta'((q, \varepsilon), c, X) = \{((q, \mathrm{h}(c)), X) \mid c \in \Sigma, q \in Q, X \in \Gamma \}</tex>. Когда буфер пуст, <tex> M' </tex> может прочитать свой следующий входной символ <tex> c </tex> и поместить <tex> \mathrm{h}(c) </tex> в буфер. |
| − | ** | + | ** Если <tex> (p, \gamma) \in \delta(q, b, X), b \in T \cup \varepsilon </tex>, то <tex> ((p, x), \gamma) \in \delta'((q, bx), \varepsilon, X) </tex>. Таким образом, <tex> M' </tex> всегда имеет возможность имитации перехода <tex> M </tex>, используя голову буфера. Если <tex> b \in T </tex>, то буфер должен быть непустым, но если <tex> b = \varepsilon </tex>, то буфер может быть пустым. |
| − | * | + | * Начальным состоянием <tex> M' </tex> является <tex> (s, \varepsilon) </tex>, т.е. <tex> M' </tex> стартует в начальном состоянии <tex> M </tex> с пустым буфером. |
| − | * | + | * Допускающими состояниями <tex> M' </tex> являются состояния <tex> (q, \varepsilon)</tex>, где <tex> q \in T </tex>. |
| − | Таким образом получаем, что <tex>(s, h(w), Z_0) \vdash_M^{*} (p, \varepsilon, \gamma) \Leftrightarrow ((s, \varepsilon), w, Z_0) \vdash_{M'}^{*} ((p, \varepsilon), \varepsilon, \gamma)</tex> | + | Таким образом получаем, что <tex>(s, \mathrm{h}(w), Z_0) \vdash_M^{*} (p, \varepsilon, \gamma) \Leftrightarrow ((s, \varepsilon), w, Z_0) \vdash_{M'}^{*} ((p, \varepsilon), \varepsilon, \gamma)</tex>, то есть автомат <tex> M' </tex> допускает те и только те слова, которые принадлежат языку <tex> \mathrm{h^{-1}}(L) </tex>. |
| + | }} | ||
=== Разворот === | === Разворот === | ||
| − | + | {{ Утверждение | |
| + | |statement= <tex> L^{R} = \{ w^{R} \mid w \in L \}</tex> контекстно-свободен. | ||
| + | |proof= | ||
| + | Для того, чтобы построить <tex> L^{R} </tex>, необходимо развернуть все правые части правил грамматики для <tex> L </tex>. | ||
| + | |||
| + | Покажем, что <tex>w \in L \iff w^{R} \in L^{R}</tex>. | ||
| + | |||
| + | <tex>\Rightarrow</tex> | ||
| + | :Докажем с помощью метода математической индукции по длине порождения в грамматике <tex>L</tex>. | ||
| + | :'''База'''. <tex>A \underset{L}{\Rightarrow} w</tex>. | ||
| + | |||
| + | :: В грамматике <tex>L</tex> существует правило <tex>A \rightarrow w</tex> и, так как мы развернули все правые части правил, то <tex>A \underset{L^{R}}{\Rightarrow} w^{R}</tex>. | ||
| − | + | :'''Предположение индукции'''. Пусть <tex>A \underset{L}{\Rightarrow}^* w</tex> менее чем за <tex>n</tex> шагов, тогда <tex>A \underset{L^{R}}{\Rightarrow}^* w^{R}</tex>. | |
| − | + | :'''Переход'''. | |
| + | :: Пусть в порождении <tex>n</tex> шагов, <tex>n > 1</tex>. Тогда оно имеет вид <tex>A \underset{L}{\Rightarrow}Y_1 Y_2 \ldots Y_m \underset{L}{\Rightarrow}^*w</tex>, где <tex> Y_i \in N \cup \Sigma </tex>. Цепочку <tex> w </tex> можно разбить на <tex>w_1 w_2 \ldots w_m</tex>, где <tex> Y_i \underset{L}{\Rightarrow}^*w_i</tex>. Так как каждое из порождений <tex> Y_i \underset{L}{\Rightarrow}^*w_i </tex> содержит менее <tex> n </tex> шагов, к ним можно применить предположение индукции и заключить, что <tex> Y_i \underset{L^{R}}{\Rightarrow}^*w_i^{R} </tex>. Так как <tex>A \underset{L}{\Rightarrow}Y_1 Y_2 \ldots Y_m</tex>, то <tex>A \underset{L^{R}}{\Rightarrow}Y_m Y_{m - 1} \ldots Y_1</tex>, откуда следует, что <tex> A \underset{L^{R}}{\Rightarrow}^* w^{R} </tex>. | ||
| + | |||
| + | <tex>\Leftarrow</tex> | ||
| + | :Доказательство аналогично. | ||
| + | }} | ||
| + | '''Пример разворота''': | ||
| + | |||
| + | Пусть задана КС-грамматика <tex>G</tex> для языка <tex>L = a^i b^j c^i</tex> со следующими правилами: | ||
| + | |||
| + | * <tex> A \to bA \mid \varepsilon </tex> | ||
| + | * <tex> B \to aBc \mid A </tex> | ||
| + | |||
| + | В таком случае КС-грамматика <tex>G^R</tex> для языка <tex>L^R = c^i b^j a^i </tex> выглядит следующим образом: | ||
| + | |||
| + | * <tex> A \to Ab \mid \varepsilon </tex> | ||
| + | * <tex> B \to cBa \mid A </tex> | ||
| + | |||
| + | === Дополнение к языку тандемных повторов === | ||
{{ Утверждение | {{ Утверждение | ||
| − | |statement= <tex> L = \{ww \mid w \in \Sigma^{*} \} </tex> не является КС-языком | + | |statement= Язык тандемных повторов <tex> L = \{ww \mid w \in \Sigma^{*} \} </tex> не является КС-языком. |
|proof= | |proof= | ||
| + | Это доказывается с помощью [[Лемма о разрастании для КС-грамматик|леммы о разрастании]]. | ||
| + | }} | ||
| + | {{ Утверждение | ||
| + | |statement= Дополнение к языку тандемных повторов <tex>\overline{L}</tex> является КС-языком. | ||
| + | |proof= | ||
| + | Для упрощения рассмотрим этот язык на бинарном алфавите <tex>\Sigma = \{a,b\}</tex>. | ||
| + | Для <tex> \overline{L} </tex> можно составить следующую [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|КС-грамматику]] <tex>G</tex>: | ||
| + | |||
| + | * <tex>S \to AB \mid BA</tex> | ||
| + | * <tex>S \to A \mid B</tex> | ||
| + | * <tex>S \to \varepsilon </tex> | ||
| + | * <tex>A \to aAa \mid aAb \mid bAa \mid bAb \mid a </tex> | ||
| + | * <tex>B \to aBa \mid aBb \mid bBa \mid bBb \mid b </tex> | ||
| + | |||
| + | Докажем этот факт. | ||
| + | |||
| + | Сначала заметим, что нетерминал <tex>A</tex> порождает слова нечётной длины с центральным символом <tex>a</tex>. В свою очередь нетерминал <tex>B</tex> порождает слова нечётной длины с центральным символом <tex>b</tex>. Таким образом, правило <tex>S \to A \mid B</tex> порождает все возможные слова нечётной длины. | ||
| + | |||
| + | '''Докажем, что все слова, порождённые <tex>G</tex>, есть в <tex>\overline{L}</tex>.''' | ||
| + | |||
| + | <tex>\varepsilon</tex>, а также все слова нечётной длины не являются тандемными повторами. | ||
| + | |||
| + | Рассмотрим произвольное слово чётной длины, сгенерированное при помощи правила <tex>S \to AB </tex>. Пусть его часть, соответствующая <tex>A</tex>, имеет длину <tex>2N+1</tex>, а часть, соответствующая <tex>B</tex>, {{---}} длину <tex>2M+1</tex>. | ||
| + | |||
| + | [[Файл:TandemRepeatAB.png]] | ||
| + | |||
| + | Таким образом, мы получили слово длины <tex>2N+2M+2</tex>. Если оно является тандемным повтором, то символ, стоящий на позиции <tex>N+1</tex>, должен быть равен символу на позиции <tex>2N+M+2</tex>. Но по построению это не так. | ||
| + | |||
| + | Для правила <tex>S \to BA </tex> доказательство аналогично. | ||
| + | |||
| + | '''Докажем, что все слова из <tex>\overline{L}</tex> порождаются <tex>G</tex>.''' | ||
| + | |||
| + | С помощью <tex>G</tex> можно вывести <tex> \varepsilon</tex>, а также любое слово нечётной длины. | ||
| + | |||
| + | Далее рассмотрим произвольное слово чётной длины из <tex>\overline{L}</tex>. Докажем, что его можно разбить на два слова нечётной длины, имеющие различные центральные символы. Предположим, что это не так, то есть такого разбиения нет. | ||
| + | |||
| + | Пусть это слово имеет длину <tex>2N</tex>. Тогда рассмотрим все его префиксы нечётной длины. Их центры находятся на позициях <tex>1, 2, \ldots ,N</tex>, а центры соответствующих им суффиксов {{---}} на позициях <tex>N+1, N+2, \ldots ,2N</tex>. Поскольку искомого разбиения не существует, то получается, что символ на позиции <tex>1</tex> равен символу на позиции <tex>N+1</tex>, символ на позиции <tex>2</tex> равен символу на позиции <tex>N+2</tex>, и так далее. Следовательно, первая половина слова равна его второй половине, т.е. оно является тандемных повтором. | ||
| + | |||
| + | Получили противоречие, следовательно любое слово чётной длины из <tex>\overline{L}</tex> можно разделить на два слова нечётной длины с различными центральными символами. В свою очередь, такие слова могут быть сгенерированы при помощи грамматики <tex>G</tex> и соединены при помощи правила <tex>S \to AB \mid BA</tex>. | ||
| − | |||
}} | }} | ||
| + | |||
| + | === Пересечение === | ||
{{ Утверждение | {{ Утверждение | ||
|statement= Если <tex> L_1 = a^i b^i c^j , L_2 = a^i b^j c^j </tex>, то <tex> L_1 \cap L_2 </tex> не является КС-языком. | |statement= Если <tex> L_1 = a^i b^i c^j , L_2 = a^i b^j c^j </tex>, то <tex> L_1 \cap L_2 </tex> не является КС-языком. | ||
|proof= | |proof= | ||
| − | <tex> L_1 = \{ a^i b^i \} | + | <tex> L_1 = \{ a^i b^i \} \{ c^j \}, L_2 = \{ a^i \} \{ b^j c^j \} </tex> |
| + | |||
| + | По замкнутости КС-языков относительно конкатенации получаем, что <tex> L_1 </tex> и <tex> L_2 </tex> являются КС-языками. | ||
| − | Но <tex> L_1 \cap L_2 = \{ a^i b^i c^i \mid i \in \mathbb{N} \} </tex>, | + | Но <tex> L_1 \cap L_2 = \{ a^i b^i c^i \mid i \in \mathbb{N} \} </tex>, который по [[Лемма о разрастании для КС-грамматик|лемме о разрастании]] для КС-языков не является КС-языком. |
}} | }} | ||
| − | + | === Разность === | |
| + | {{ Утверждение | ||
| + | |statement= КС-языки не замкнуты относительно разности. | ||
| + | |proof= | ||
| + | <tex> L_1 \setminus L_2 = L_1 \cap \overline{L_2} </tex> | ||
| + | }} | ||
Более того, задачи определения того, является ли дополнение КС-языка КС-языком и проверки непустоты пересечения КС-языков являются алгоритмически [[Разрешимые (рекурсивные) языки|неразрешимыми]]. | Более того, задачи определения того, является ли дополнение КС-языка КС-языком и проверки непустоты пересечения КС-языков являются алгоритмически [[Разрешимые (рекурсивные) языки|неразрешимыми]]. | ||
| − | === | + | === Половины тандемных повторов === |
{{ Определение | {{ Определение | ||
|definition= | |definition= | ||
| − | <tex> \mathrm{ | + | <tex> \mathrm{half}(L) = \{ w \mid ww \in L \} </tex> |
}} | }} | ||
| − | Операция <tex> \mathrm{ | + | {{ Утверждение |
| + | |statement= Операция <tex> \mathrm{half} </tex> не сохраняет КС-язык таковым. | ||
| + | |proof= | ||
| + | Покажем это на примере. Рассмотрим язык <tex> L = \{ a^n b a^n b a^m b a^l b a^k b a^k b \} </tex>. | ||
| + | |||
| + | Заметим, что он может быть сгенерирован при помощи следующей КС-грамматики: | ||
| + | |||
| + | * <tex> S \to AbBbBbAb </tex> | ||
| + | * <tex> B \to a \mid aB</tex> | ||
| + | * <tex> A \to b \mid aAa</tex> | ||
| + | |||
| + | '''Докажем, что <tex> \mathrm{half}(L) </tex> не является КС-языком.''' | ||
| + | |||
| + | Пусть <tex> \alpha = a^n b a^n b a^m b a^l b a^k b a^k b = ww </tex>. Отсюда следует, что: | ||
* <tex> n = l </tex> | * <tex> n = l </tex> | ||
* <tex> n = k </tex> | * <tex> n = k </tex> | ||
* <tex> m = k </tex> | * <tex> m = k </tex> | ||
| − | А значит, <tex> n = l = k = m </tex>, и <tex> \mathrm{ | + | А значит, <tex> n = l = k = m </tex>, и <tex> \mathrm{half}(L) = \{ a^n b a^n b a^n b \} </tex>, и по [[Лемма о разрастании для КС-грамматик|лемме о разрастании]] КС-языком не является. |
| − | + | }} | |
== Операции над КС-языком и регулярным языком == | == Операции над КС-языком и регулярным языком == | ||
=== Пересечение === | === Пересечение === | ||
| − | + | {{Утверждение | |
| − | + | |statement = Пересечение КС-языка и [[Регулярные языки: два определения и их эквивалентность|регулярного языка]] — КС-язык. | |
| + | |proof = | ||
| + | Построим МП-автомат для пересечения регулярного языка и КС-языка. | ||
Пусть регулярный язык задан своим [[Детерминированные конечные автоматы|ДКА]], а КС-язык — своим [[Автоматы с магазинной памятью|МП-автоматом]] c допуском по допускающему состоянию. Построим прямое произведение этих автоматов так же, как строилось прямое произведение для двух ДКА. | Пусть регулярный язык задан своим [[Детерминированные конечные автоматы|ДКА]], а КС-язык — своим [[Автоматы с магазинной памятью|МП-автоматом]] c допуском по допускающему состоянию. Построим прямое произведение этих автоматов так же, как строилось прямое произведение для двух ДКА. | ||
| Строка 114: | Строка 219: | ||
Этот автомат использует в качестве состояний пары из двух состояний каждого автомата, а за операции со стеком отвечает только МП-автомат. Слово допускается этим автоматом <tex> \iff </tex> слово допускается и ДКА и МП-автоматом, то есть язык данного автомата совпадает с <tex> R \cap L </tex>. | Этот автомат использует в качестве состояний пары из двух состояний каждого автомата, а за операции со стеком отвечает только МП-автомат. Слово допускается этим автоматом <tex> \iff </tex> слово допускается и ДКА и МП-автоматом, то есть язык данного автомата совпадает с <tex> R \cap L </tex>. | ||
| + | }} | ||
| + | === Разность === | ||
| + | {{ Утверждение | ||
| + | |statement= Разность КС-языка и регулярного языка — КС-язык. | ||
| + | |proof= | ||
| + | <tex> L \setminus R = L \cap \overline{R} </tex> | ||
| − | === | + | Регулярные языки замкнуты относительно дополнения, следовательно разность можно выразить через пересечение. |
| + | }} | ||
| + | == См. также == | ||
| + | * [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора]] | ||
| + | * [[Замкнутость регулярных языков относительно различных операций]] | ||
| + | * [[Основные определения, связанные со строками]] | ||
| + | == Источники информации == | ||
| − | + | * ''Хопкрофт Д., Мотвани Р., Ульман Д.'' — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — C. 302-304 : ISBN 5-8459-0261-4 (рус.) | |
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Контекстно-свободные грамматики]] | [[Категория: Контекстно-свободные грамматики]] | ||
| + | [[Категория: Базовые понятия о грамматиках]] | ||
Текущая версия на 19:29, 4 сентября 2022
В отличие от регулярных языков, КС-языки не замкнуты относительно всех теоретико-множественных операций. К примеру, дополнение и пересечение КС-языков не обязательно являются КС-языками.
Здесь и далее считаем, что и — КС-языки.
Содержание
Операции с КС-языками
Объединение
| Утверждение: |
является КС-языком. |
|
Построим КС-грамматику для языка . Для этого рассмотрим соответствующие КС-грамматики для языков и . Пусть стартовые символы в них имеют имена и соответственно. Тогда стартовый символ для обозначим за и добавим правило . Покажем, что .
|
Конкатенация
| Утверждение: |
— КС-язык. |
| Аналогично предыдущему случаю построим КС-грамматику для языка . Для этого добавим правило , где и — стартовые символы языков и соответственно. |
Замыкание Клини
| Утверждение: |
— КС-язык. |
| Если — стартовый символ КС-грамматики для языка , то добавим в КС-грамматику для языка новый стартовый символ и правила . |
Гомоморфизмы
Прямой гомоморфизм
| Утверждение: |
КС-языки замкнуты относительно прямого гомоморфизма. |
| Построим КС-грамматику, в которой каждый символ заменим на . |
Обратный гомоморфизм
| Утверждение: |
КС-языки замкнуты относительно обратного гомоморфизма. |
|
Докажем аналогично соответствующему утверждению для регулярных языков. Построим МП-автомат для на основе МП-автомата для языка (назовем его ). Новый автомат будет действовать следующим образом:
Если рассмотреть более формально, пусть , тогда .
|
Разворот
| Утверждение: |
контекстно-свободен. |
|
Для того, чтобы построить , необходимо развернуть все правые части правил грамматики для . Покажем, что .
|
Пример разворота:
Пусть задана КС-грамматика для языка со следующими правилами:
В таком случае КС-грамматика для языка выглядит следующим образом:
Дополнение к языку тандемных повторов
| Утверждение: |
Язык тандемных повторов не является КС-языком. |
| Это доказывается с помощью леммы о разрастании. |
| Утверждение: |
Дополнение к языку тандемных повторов является КС-языком. |
|
Для упрощения рассмотрим этот язык на бинарном алфавите . Для можно составить следующую КС-грамматику : Докажем этот факт. Сначала заметим, что нетерминал порождает слова нечётной длины с центральным символом . В свою очередь нетерминал порождает слова нечётной длины с центральным символом . Таким образом, правило порождает все возможные слова нечётной длины. Докажем, что все слова, порождённые , есть в . , а также все слова нечётной длины не являются тандемными повторами. Рассмотрим произвольное слово чётной длины, сгенерированное при помощи правила . Пусть его часть, соответствующая , имеет длину , а часть, соответствующая , — длину . Таким образом, мы получили слово длины . Если оно является тандемным повтором, то символ, стоящий на позиции , должен быть равен символу на позиции . Но по построению это не так. Для правила доказательство аналогично. Докажем, что все слова из порождаются . С помощью можно вывести , а также любое слово нечётной длины. Далее рассмотрим произвольное слово чётной длины из . Докажем, что его можно разбить на два слова нечётной длины, имеющие различные центральные символы. Предположим, что это не так, то есть такого разбиения нет. Пусть это слово имеет длину . Тогда рассмотрим все его префиксы нечётной длины. Их центры находятся на позициях , а центры соответствующих им суффиксов — на позициях . Поскольку искомого разбиения не существует, то получается, что символ на позиции равен символу на позиции , символ на позиции равен символу на позиции , и так далее. Следовательно, первая половина слова равна его второй половине, т.е. оно является тандемных повтором. Получили противоречие, следовательно любое слово чётной длины из можно разделить на два слова нечётной длины с различными центральными символами. В свою очередь, такие слова могут быть сгенерированы при помощи грамматики и соединены при помощи правила . |
Пересечение
| Утверждение: |
Если , то не является КС-языком. |
|
По замкнутости КС-языков относительно конкатенации получаем, что и являются КС-языками. Но , который по лемме о разрастании для КС-языков не является КС-языком. |
Разность
| Утверждение: |
КС-языки не замкнуты относительно разности. |
Более того, задачи определения того, является ли дополнение КС-языка КС-языком и проверки непустоты пересечения КС-языков являются алгоритмически неразрешимыми.
Половины тандемных повторов
| Определение: |
| Утверждение: |
Операция не сохраняет КС-язык таковым. |
|
Покажем это на примере. Рассмотрим язык . Заметим, что он может быть сгенерирован при помощи следующей КС-грамматики: Докажем, что не является КС-языком. Пусть . Отсюда следует, что: |
Операции над КС-языком и регулярным языком
Пересечение
| Утверждение: |
Пересечение КС-языка и регулярного языка — КС-язык. |
|
Построим МП-автомат для пересечения регулярного языка и КС-языка. Пусть регулярный язык задан своим ДКА, а КС-язык — своим МП-автоматом c допуском по допускающему состоянию. Построим прямое произведение этих автоматов так же, как строилось прямое произведение для двух ДКА. Более формально, пусть — регулярный язык, заданный своим ДКА , и — КС-язык, заданный своим МП-автоматом: . Тогда прямым произведением назовем следующий автомат:
видя на ленте символ и символ на вершине стека. Этот автомат использует в качестве состояний пары из двух состояний каждого автомата, а за операции со стеком отвечает только МП-автомат. Слово допускается этим автоматом слово допускается и ДКА и МП-автоматом, то есть язык данного автомата совпадает с . |
Разность
| Утверждение: |
Разность КС-языка и регулярного языка — КС-язык. |
|
Регулярные языки замкнуты относительно дополнения, следовательно разность можно выразить через пересечение. |
См. также
- Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора
- Замкнутость регулярных языков относительно различных операций
- Основные определения, связанные со строками
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — C. 302-304 : ISBN 5-8459-0261-4 (рус.)