Регулярная аппроксимация КС-языков — различия между версиями
(→Источники) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 76 промежуточных версий 7 участников) | |||
| Строка 18: | Строка 18: | ||
{{Лемма | {{Лемма | ||
|statement = Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык. | |statement = Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык. | ||
| − | |proof = В качестве конструктивного доказательства | + | |proof = В качестве конструктивного доказательства рассмотрим алгоритм построения [[Недетерминированные конечные автоматы|конечного автомата]] по грамматике. Также приведем ссылку на формальное доказательство<ref>[http://ac.els-cdn.com/S0019995859800176/1-s2.0-S0019995859800176-main.pdf?_tid=01067c30-c616-11e6-a178-00000aab0f6c&acdnat=1482171029_8a3a81a6f520cf0f9a769aaafbb8babb Noam Chomsky {{---}} A note on phrase structure grammars]</ref>. |
}} | }} | ||
=== Идея алгоритма === | === Идея алгоритма === | ||
| − | Пусть, <tex> N^* </tex> множество рекурсивных | + | Пусть, <tex> N^* </tex> множество рекурсивных нетерминалов из <tex> N </tex>. |
| − | Пусть, <tex> P = \{N_1,N_2, | + | Пусть, <tex> P = \{N_1,N_2,\ldots,N_K\} </tex> разбиение <tex> N^*</tex> на <tex> k </tex> дизъюнктных множеств взаимно рекурсивных нетерминалов, |
| − | <tex> N_1 \cup N_2 \cup | + | <tex> N_1 \cup N_2 \cup \ldots \cup N_k = N^* \land \forall i</tex> <tex> N_i \neq \emptyset </tex>. |
| − | + | ||
| − | ''' | + | Определим вспомогательную функцию <tex>\mathtt {isLeftType}(N_i)</tex>, которая возвращает <tex>true</tex>, если существует <tex> (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ]</tex>. |
| + | |||
| + | Аналогично определим функцию <tex>\mathtt {isRightType}(N_i)</tex>, которая возвращает <tex>true</tex>, если существует <tex> (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ]</tex> | ||
| + | '''bool''' isLeftType(<tex>N_i</tex>: '''nonterminal'''): | ||
'''return''' <tex> \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ]</tex> | '''return''' <tex> \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \alpha \neq \varepsilon ]</tex> | ||
| − | ''' | + | '''bool''' isRightType(<tex>N_i</tex>: '''nonterminal'''): |
'''return''' <tex> \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ]</tex> | '''return''' <tex> \exists (A \Rightarrow \alpha B \beta) \in P[ A \in N_i \land B \in N_i \land \beta \neq \varepsilon ]</tex> | ||
| + | Будем называть <tex>\mathtt {typeRecursive}</tex> набор четырех величин <tex>\{left, right, self, cycle\} </tex> | ||
| − | + | Определим функцию <tex>\mathtt {getTheTypeOfMutualRecursiveSet}(N_i): P \rightarrow \mathtt {typeRecursive} </tex>: | |
| − | '''function''' | + | '''function''' getTheTypeOfMutualRecursiveSet(<tex>N_i</tex>: '''nonterminal'''): '''typeRecurcive''' |
| − | '''if''' ! | + | '''if''' !isLeftType(<tex>N_i</tex>) '''and''' isRightType(<tex>N_i</tex>) |
| − | return left | + | '''return''' left |
| − | '''if''' | + | '''if''' isLeftType(<tex>N_i</tex>) '''and''' !isRightType(<tex>N_i</tex>) |
| − | return right | + | '''return''' right |
| − | '''if''' | + | '''if''' isLeftType(<tex>N_i</tex>) '''and''' isRightType(<tex>N_i</tex>) |
| − | return self | + | '''return''' self |
| − | '''if''' ! | + | '''if''' !isLeftType(<tex>N_i</tex>) '''and''' !isRightType(<tex>N_i</tex>) |
| − | return cyclic | + | '''return''' cyclic |
| − | Заметим, что <tex> \forall i </tex> <tex> | + | :Состояние <tex> left</tex> означает, что <tex> N_i </tex> состоит только из лево-рекурсивных нетерминалов. |
| − | В основе алгоритма будет рекурсивный обход грамматики | + | :Состояние <tex> right</tex> означает, что <tex> N_i </tex> состоит только из право-рекурсивных нетерминалов. |
| − | # | + | :Состояние <tex> cyclic</tex> означает, что <tex> N_i </tex> состоит только из правил, участвующих в рекурсии. |
| − | # | + | :Состояние <tex> self</tex> означает, что <tex>i </tex> такое, при котором грамматика самоприменима. |
| − | # | + | Заметим, что <tex> \forall i </tex> <tex>\mathtt {getTheTypeOfMutualRecursiveSet}(N_i) \neq self </tex>, т.к в противном случае грамматика будет самоприменима. |
| + | В основе алгоритма будет рекурсивный обход грамматики. Спускаемся по грамматике до тех пор не приходим в нетерминал или символ алфавита: | ||
| + | # Символ алфавит или <tex> \varepsilon </tex> {{---}} добавляем новое правило в автомат; | ||
| + | # Нерекурсивный нетерминал {{---}} запускаемся от всех правых частей правил, который терминал порождает; | ||
| + | # Рекурсивный нетерминал {{---}} в зависимости от типа рекурсивного нетерминала, продолжаем рекурсию (будет ясно из пседокода). | ||
===Псевдокод=== | ===Псевдокод=== | ||
<tex>Q</tex> {{---}} множество состояний ДКА. | <tex>Q</tex> {{---}} множество состояний ДКА. | ||
| + | |||
<tex>\Delta</tex> {{---}} множество переходов ДКА. | <tex>\Delta</tex> {{---}} множество переходов ДКА. | ||
| + | |||
<tex>T</tex> {{---}} множество допускающих состояний. | <tex>T</tex> {{---}} множество допускающих состояний. | ||
| − | '''function''' createFA(G) // <tex> G = \langle N, \Sigma, P, S \rangle</tex> | + | '''function''' createFA(G: '''grammar'''): '''Automaton''' <font color=green>// <tex> G = \langle N, \Sigma, P, S \rangle</tex> </font> |
<tex>\mathtt{Q} \leftarrow \varnothing</tex> | <tex>\mathtt{Q} \leftarrow \varnothing</tex> | ||
<tex>\Delta \leftarrow \varnothing </tex> | <tex>\Delta \leftarrow \varnothing </tex> | ||
| − | s = createState | + | s = createState() <font color=green>// createState создает некоторый объект, не принадлежащий <tex>Q</tex>, возвращает этот объект и добавляет его в <tex>Q</tex> </font> |
| − | f = createState | + | f = createState() |
<tex>F \leftarrow \{f\} </tex> | <tex>F \leftarrow \{f\} </tex> | ||
| − | '''return''' makeFA (s,S,f) | + | '''return''' makeFA(s,S,f) |
| − | '''function''' makeFA (q0,a,q1) | + | '''function''' makeFA(q0: '''vertex''', a: '''char''', q1: '''vertex'''): '''Automaton''' |
| − | '''if''' a == <tex> \varepsilon </tex> | + | '''if''' a == <tex> \varepsilon </tex> '''or''' a <tex> \in \Sigma</tex> <font color=green>// пришли в лист дерева разбора</font> |
<tex> \Delta = \Delta \cup \{(q_0,a,q_1)\} </tex> | <tex> \Delta = \Delta \cup \{(q_0,a,q_1)\} </tex> | ||
'''return''' | '''return''' | ||
'''if''' a == <tex>X\beta</tex> '''where''' <tex> X \in (N \cup \Sigma) \land \beta \in (N \cup \Sigma)^* \land |\beta| > 0 </tex> | '''if''' a == <tex>X\beta</tex> '''where''' <tex> X \in (N \cup \Sigma) \land \beta \in (N \cup \Sigma)^* \land |\beta| > 0 </tex> | ||
| − | q = createState | + | q = createState() |
| − | makeFA (<tex>q_0,X,q_1</tex>) | + | makeFA(<tex>q_0,X,q_1</tex>) |
| − | makeFA (<tex>q, \beta, q_1 </tex>) | + | makeFA(<tex>q, \beta, q_1 </tex>) |
'''return''' | '''return''' | ||
'''if''' '''exist''' <tex> N_i </tex> '''where''' <tex> a \in N_i </tex> | '''if''' '''exist''' <tex> N_i </tex> '''where''' <tex> a \in N_i </tex> | ||
'''foreach''' b '''in''' <tex>N_i</tex> | '''foreach''' b '''in''' <tex>N_i</tex> | ||
<tex>q_b</tex> = createState | <tex>q_b</tex> = createState | ||
| − | '''if | + | '''if''' getTheTypeOfMutualRecursiveSet(<tex> N_i </tex>) == left |
| − | '''foreach''' C '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow X_1 | + | '''foreach''' C '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow X_1 \ldots X_m \land X_1, \ldots X_m \neq N_i </tex> |
| − | makeFA (<tex>q_0, X_1 \ | + | makeFA(<tex>q_0, X_1 \ldots X_m, q_C</tex>) |
| − | '''foreach''' C,D '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow DX_1 | + | '''foreach''' C,D '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow DX_1 \ldots X_m \land X_1, \ldots X_m \neq N_i </tex> |
| − | makeFA (<tex>q_D, X_1 \ | + | makeFA(<tex>q_D, X_1 \ldots X_m, q_C</tex>) |
<tex> \Delta = \Delta \cup \{(q_a,\varepsilon,q_1)\} </tex> | <tex> \Delta = \Delta \cup \{(q_a,\varepsilon,q_1)\} </tex> | ||
| − | '''else''' | + | '''else''' <font color=green>// рекурсивный нетерминал right или cyclic</font> |
| − | '''foreach''' C '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow X_1 | + | '''foreach''' C '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow X_1 \ldots X_m \land X_1, \ldots X_m \neq N_i </tex> |
| − | makeFA (<tex>q_C, X_1 \ | + | makeFA(<tex>q_C, X_1 \ldots X_m, q_1</tex>) |
| − | '''foreach''' C,D '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow DX_1 | + | '''foreach''' C,D '''in''' <tex>N_i</tex> '''where''' <tex> C \rightarrow DX_1 \ldots X_m \land X_1, \ldots X_m \neq N_i </tex> |
| − | makeFA (<tex>q_D, X_1 \ | + | makeFA(<tex>q_D, X_1 \ldots X_m, q_C</tex>) |
<tex> \Delta = \Delta \cup \{(q_0, \varepsilon ,q_a)\} </tex> | <tex> \Delta = \Delta \cup \{(q_0, \varepsilon ,q_a)\} </tex> | ||
'''return''' | '''return''' | ||
'''foreach''' p '''in''' <tex>P</tex> '''where''' p == <tex> a \rightarrow \beta </tex> | '''foreach''' p '''in''' <tex>P</tex> '''where''' p == <tex> a \rightarrow \beta </tex> | ||
| − | makeFA (<tex> q_0, \beta, q_1 </tex>) | + | makeFA(<tex> q_0, \beta, q_1 </tex>) |
== Аппроксимации самоприменимой грамматики == | == Аппроксимации самоприменимой грамматики == | ||
| − | В данном разделе покажем методы апроксимации самоприменимой | + | В данном разделе покажем методы апроксимации: <tex>\mathrm {RTN}</tex> (''recursive transition network'') аппроксимацию и <tex>\mathrm {MN}</tex> (''Mohri and Nederhof's'') аппроксимацию — самоприменимой контекстно-свободной грамматики <tex> G = \langle N, \Sigma, P, S \rangle</tex> к регулярной грамматике. Для удобства будем считать, что грамматика представлена в [[Нормальная форма Хомского|НФХ]]. |
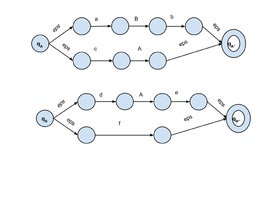
[[Файл:RTN_Automat.png|280px|thumb|right|Автоматы <tex>T_A,T_B</tex> для грамматики | [[Файл:RTN_Automat.png|280px|thumb|right|Автоматы <tex>T_A,T_B</tex> для грамматики | ||
<tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | <tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | ||
=== RTN аппроксимация === | === RTN аппроксимация === | ||
Построим, по данной грамматике аппроксимирующий ее конечный автомат. | Построим, по данной грамматике аппроксимирующий ее конечный автомат. | ||
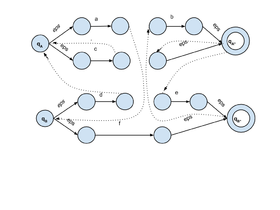
| − | [[Файл:RTN_Automat1.png|280px|thumb| | + | [[Файл:RTN_Automat1.png|280px|thumb|right|Конечный автомат для грамматики |
<tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | <tex>A \rightarrow aBb \\ A \rightarrow cA \\ B \rightarrow dAe \\ B \rightarrow f </tex>]] | ||
#Для каждого нетерминала <tex> A</tex> в грамматике, создадим новый конечный автомат <tex> T_A</tex>, добавим в него два состояния <tex> q_A</tex> и <tex>q_{A^*}</tex>. | #Для каждого нетерминала <tex> A</tex> в грамматике, создадим новый конечный автомат <tex> T_A</tex>, добавим в него два состояния <tex> q_A</tex> и <tex>q_{A^*}</tex>. | ||
| − | #Для каждого правила грамматике <tex> (A \rightarrow X_1 \ | + | #Для каждого правила грамматике <tex> (A \rightarrow X_1 \ldots X_m ) \in P</tex>, введм новые состояния в автомат этого нетерминала <tex> q_0^A \ldots q_m^A</tex>, а также добавим новые правила перехода в <tex> \Delta</tex>: <tex> (q_A, \varepsilon, q_0),(q_0^A,X_1,q_1^A), \ldots,(q_{m-1}^A,X_m,q_m^A),(q_m^A,\varepsilon,q_{A^*})</tex>. |
| − | #Таким образом мы построили множество конечных автоматов <tex>T</tex> = <tex> \{ T_A \ | + | #Таким образом мы построили множество конечных автоматов <tex>T</tex> = <tex> \{ T_A \mid A \in N\}</tex> для каждого нетерминала <tex>A</tex>. Теперь объединим все в один автомат. Объединим все состоянии автоматов из <tex>T</tex> в множество <tex>Q</tex>. Скопируем все переходы каждого автомата из <tex>T</tex> в <tex>\Delta</tex>. Далее для каждого перехода вида <tex>(q,A,p), A\in N</tex>, вместо него добавим два новых перехода: <tex> (q, \varepsilon, q_A),(q_A^{*}, \varepsilon, p) </tex>. |
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===MN аппроксимация === | ||
| + | Построим по данной самоприменимой контекстно-свободной грамматике <tex> G </tex> регулярную грамматику <tex> G^*</tex>. | ||
| + | #Для каждого нетерминала <tex> A \in N </tex> из <tex>G</tex>, добавим нетерминалы <tex>A</tex> и <tex> A^*</tex> в <tex> G^* </tex>. | ||
| + | #Для каждого правила <tex> A \rightarrow {\alpha}_{0} B_1 {\alpha}_{1} B_2 {\alpha}_{2} \ldots B_m {\alpha}_{m}</tex>, где <tex> B_1, \ldots, B_m \in N \land {\alpha}_i \in \Sigma^*</tex>. Добавим в <tex> G^*</tex> нетерминалы <tex> B_1 \ldots B_m , B_1^* \ldots B_m^*</tex> и следуюшие правила: <tex>\begin{cases} A \rightarrow {\alpha}_0 B_1 \\ B_1^* \rightarrow {\alpha}_1 B_2\\ \ldots \\ B^*_m \rightarrow {\alpha}_m A^* \end{cases}</tex>. | ||
| + | :(Если <tex>m = 0 </tex>, тогда добавим правило <tex> A \rightarrow {\alpha}_0 A^* </tex>). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
В итоге <tex> G^*</tex> {{---}} [[Правоконтекстные грамматики, эквивалентность автоматам|правоконтекстная грамматика]], эквивалентная конечному автомату, который задает регулярный язык. | В итоге <tex> G^*</tex> {{---}} [[Правоконтекстные грамматики, эквивалентность автоматам|правоконтекстная грамматика]], эквивалентная конечному автомату, который задает регулярный язык. | ||
==== Пример ==== | ==== Пример ==== | ||
| − | <tex> G = | + | <tex> G = \begin{cases} A \rightarrow \alpha B \alpha |
\\ B \rightarrow \beta A | \beta | \\ B \rightarrow \beta A | \beta | ||
| − | \end{ | + | \end{cases}\Rightarrow |
| + | G^* = \begin{cases} A \rightarrow \alpha B | ||
\\ A^* \rightarrow B^* | \varepsilon | \\ A^* \rightarrow B^* | \varepsilon | ||
\\ B \rightarrow \beta A | \beta B^* | \\ B \rightarrow \beta A | \beta B^* | ||
\\ B^* \rightarrow \alpha A^* | \varepsilon | \\ B^* \rightarrow \alpha A^* | \varepsilon | ||
| − | \end{ | + | \end{cases}</tex> |
| + | |||
| + | Исходная грамматика <tex> G </tex> генерирует язык: <tex> \{(ab)^n a^n \mid n > 0\}</tex>. Результирущая грамматика <tex> G^*</tex> генирирует регулярный язык: <tex> (ab)^+ a^*</tex>. | ||
| + | |||
| + | === Сравнение двух методов === | ||
| + | Ясно, что оба языка, генерируемых конечным автомат для первого метода и апрокисимируещей граматикой для второго метода, содержат в себе язык генерируемый исходной грамматикой. | ||
| + | Привлекателным свойством <tex>\mathrm {MN}</tex> аппроксимации по сравнению с <tex>\mathrm {RTN}</tex>, то, что она можеть быть применима к большим грамматикам: для каждого нетерминала грамматике <tex> G</tex>, добавляется не более одного нового нетерминала в <tex> G^*</tex> и размер результирующий грамматики максимум в <tex>2</tex> раза больше, чем размер исходной. Так как для <tex>\mathrm {RTN}</tex> апроксимации грамматики <tex> G = \langle N, \Sigma, P, S \rangle</tex>, количество состаяний апроксимируещего автомата в худшем случаи может составлять <tex> O(|N|^2)</tex>, что может быть критично для аппроксимации больших грамматик. | ||
| + | Также,еще несколько эффекивных методов аппрокимации можно найти в статьях, приведенных в ссылках. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора]] | ||
| + | * [[Замкнутость регулярных языков относительно различных операций]] | ||
| + | * [[Основные определения, связанные со строками]] | ||
| + | * [[Замкнутость КС-языков относительно различных операций]] | ||
| − | == | + | == Примечания == |
| − | + | <references/> | |
| − | |||
| − | * [https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CCkQFjAA&url=http%3A%2F% | + | == Источники информации== |
| + | *''Jean-Claude Junqua,Gertjan van Noord'' — Robustness in Language and Speech Technology — Kluwer Academic Publishers, 2001 — ISBN 0-7923-6790-1 | ||
| + | * [https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&ved=0CCkQFjAA&url=http%3A%2F%2Fwww.cs.ucsb.edu%2F~omer%2FDOWNLOADABLE%2Fcfg-reg09.pdf&ei=AQbcUrL_DIfi4wSx3IDYDg&usg=AFQjCNHsSWONr0_c2MDgvApwrhc81deY0w&sig2=_2iZj4Xexe6-p5Cyt-GEMg&bvm=bv.59568121,d.bGE Strongly Regular Grammars and Regular Approximation of Contex-Free Languages] | ||
| + | * [http://www.ensani.ir/storage/Files/20101126180227-431.pdf Practical Experiments with Regular Approximation of Context-Free Languages] | ||
| + | *''Willem J. M. Levelt'' — An Introduction to the Theory of Formal Languages and Automata — John Benjamin B.V., 2008 — ISBN 978-90-272-3250-2 | ||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Базовые понятия о грамматиках]] | ||
[[Категория: Контекстно-свободные грамматики]] | [[Категория: Контекстно-свободные грамматики]] | ||
Текущая версия на 19:21, 4 сентября 2022
Содержание
Определения
| Определение: |
| Контекстно-свободная грамматика называется самоприменимой (англ. self-embeded), если , . |
| Определение: |
| Нетерминал в грамматике называется рекурсивным (англ. recursive), если . |
| Определение: |
| Нетерминалы в грамматике называются взаимно рекурсивными (англ. mutual recursive), если . |
Алгоритм преобразования грамматики в конечный автомат
| Лемма: |
Не самоприменимая контекстно-свободная грамматика генерирует регулярный язык. |
| Доказательство: |
| В качестве конструктивного доказательства рассмотрим алгоритм построения конечного автомата по грамматике. Также приведем ссылку на формальное доказательство[1]. |
Идея алгоритма
Пусть, множество рекурсивных нетерминалов из . Пусть, разбиение на дизъюнктных множеств взаимно рекурсивных нетерминалов, .
Определим вспомогательную функцию , которая возвращает , если существует .
Аналогично определим функцию , которая возвращает , если существует
bool isLeftType(: nonterminal): return bool isRightType(: nonterminal): return
Будем называть набор четырех величин
Определим функцию :
function getTheTypeOfMutualRecursiveSet(: nonterminal): typeRecurcive if !isLeftType() and isRightType() return left if isLeftType() and !isRightType() return right if isLeftType() and isRightType() return self if !isLeftType() and !isRightType() return cyclic
- Состояние означает, что состоит только из лево-рекурсивных нетерминалов.
- Состояние означает, что состоит только из право-рекурсивных нетерминалов.
- Состояние означает, что состоит только из правил, участвующих в рекурсии.
- Состояние означает, что такое, при котором грамматика самоприменима.
Заметим, что , т.к в противном случае грамматика будет самоприменима. В основе алгоритма будет рекурсивный обход грамматики. Спускаемся по грамматике до тех пор не приходим в нетерминал или символ алфавита:
- Символ алфавит или — добавляем новое правило в автомат;
- Нерекурсивный нетерминал — запускаемся от всех правых частей правил, который терминал порождает;
- Рекурсивный нетерминал — в зависимости от типа рекурсивного нетерминала, продолжаем рекурсию (будет ясно из пседокода).
Псевдокод
— множество состояний ДКА.
— множество переходов ДКА.
— множество допускающих состояний.
function createFA(G: grammar): Automaton // s = createState() // createState создает некоторый объект, не принадлежащий , возвращает этот объект и добавляет его в f = createState() return makeFA(s,S,f) function makeFA(q0: vertex, a: char, q1: vertex): Automaton if a == or a // пришли в лист дерева разбора return if a == where q = createState() makeFA() makeFA() return if exist where foreach b in = createState if getTheTypeOfMutualRecursiveSet() == left foreach C in where makeFA() foreach C,D in where makeFA() else // рекурсивный нетерминал right или cyclic foreach C in where makeFA() foreach C,D in where makeFA() return foreach p in where p == makeFA()
Аппроксимации самоприменимой грамматики
В данном разделе покажем методы апроксимации: (recursive transition network) аппроксимацию и (Mohri and Nederhof's) аппроксимацию — самоприменимой контекстно-свободной грамматики к регулярной грамматике. Для удобства будем считать, что грамматика представлена в НФХ.
RTN аппроксимация
Построим, по данной грамматике аппроксимирующий ее конечный автомат.
- Для каждого нетерминала в грамматике, создадим новый конечный автомат , добавим в него два состояния и .
- Для каждого правила грамматике , введм новые состояния в автомат этого нетерминала , а также добавим новые правила перехода в : .
- Таким образом мы построили множество конечных автоматов = для каждого нетерминала . Теперь объединим все в один автомат. Объединим все состоянии автоматов из в множество . Скопируем все переходы каждого автомата из в . Далее для каждого перехода вида , вместо него добавим два новых перехода: .
MN аппроксимация
Построим по данной самоприменимой контекстно-свободной грамматике регулярную грамматику .
- Для каждого нетерминала из , добавим нетерминалы и в .
- Для каждого правила , где . Добавим в нетерминалы и следуюшие правила: .
- (Если , тогда добавим правило ).
В итоге — правоконтекстная грамматика, эквивалентная конечному автомату, который задает регулярный язык.
Пример
Исходная грамматика генерирует язык: . Результирущая грамматика генирирует регулярный язык: .
Сравнение двух методов
Ясно, что оба языка, генерируемых конечным автомат для первого метода и апрокисимируещей граматикой для второго метода, содержат в себе язык генерируемый исходной грамматикой. Привлекателным свойством аппроксимации по сравнению с , то, что она можеть быть применима к большим грамматикам: для каждого нетерминала грамматике , добавляется не более одного нового нетерминала в и размер результирующий грамматики максимум в раза больше, чем размер исходной. Так как для апроксимации грамматики , количество состаяний апроксимируещего автомата в худшем случаи может составлять , что может быть критично для аппроксимации больших грамматик. Также,еще несколько эффекивных методов аппрокимации можно найти в статьях, приведенных в ссылках.
См. также
- Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора
- Замкнутость регулярных языков относительно различных операций
- Основные определения, связанные со строками
- Замкнутость КС-языков относительно различных операций
Примечания
Источники информации
- Jean-Claude Junqua,Gertjan van Noord — Robustness in Language and Speech Technology — Kluwer Academic Publishers, 2001 — ISBN 0-7923-6790-1
- Strongly Regular Grammars and Regular Approximation of Contex-Free Languages
- Practical Experiments with Regular Approximation of Context-Free Languages
- Willem J. M. Levelt — An Introduction to the Theory of Formal Languages and Automata — John Benjamin B.V., 2008 — ISBN 978-90-272-3250-2