Атрибутные транслирующие грамматики — различия между версиями
Slavian (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 105 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Часто, осуществляя разбор, мы хотим извлечь какие-то данные или произвести какие-то действия, а не просто выяснить, разбирается ли текст в данной грамматике. | ||
| + | Вообще говоря, сначала можно получить [[Контекстно-свободные_грамматики,_вывод,_лево-_и_правосторонний_вывод,_дерево_разбора#Дерево_разбора|дерево разбора]], а потом уже, обходя его, выполнять эти действия. | ||
| + | В этом случае происходит дублирование функционала: промежуточное сохранение данных в виде дерева разбора не нужно, а иногда его просто слишком расточительно хранить в памяти целиком. | ||
| + | В связи с этим хочется какие-то действия производить уже на этапе разбора. | ||
| + | |||
| + | Например, мы хотим не только построить дерево разбора для арифметических выражений, а ещё и вычислить значение этого выражения. Возможно, даже не строя само дерево разбора. | ||
| + | |||
| + | Такой подход называется '''синтаксически управляемой трансляцией'''. | ||
| + | |||
| + | ==Синтаксически управляемая трансляция== | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Синтаксически управляемое определение''' | + | '''Синтаксически управляемое определение''' ''(англ. syntax-directed definition)'' является [[Контекстно-свободные_грамматики,_вывод,_лево-_и_правосторонний_вывод,_дерево_разбора|контекстно-свободной]] грамматикой с атрибутами и правилами. Атрибуты связаны с грамматическими символами, а правила — с продукциями. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Синтаксически управляемая трансляция''' {{---}} это трансляция, при которой в процессе разбора строки сразу выполняются какие-то действия, | + | '''Синтаксически управляемая трансляция''' ''(англ. syntax-directed translation)'' {{---}} это трансляция, при которой в [[Предиктивный_синтаксический_анализ| процессе разбора]] строки сразу выполняются какие-то действия, без использования промежуточного представления в виде дерева разбора. |
}} | }} | ||
| Строка 19: | Строка 24: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Атрибут''' {{---}} | + | '''Атрибут''' ''(англ. attribute)'' {{---}} дополнительные данные, ассоциированные с грамматическими символами. Если $X$ представляет собой символ, а $a$ — один из его атрибутов, то значение $a$ в некотором узле дерева разбора, помеченном $X$, записывается как $X.a$. Если узлы дерева разбора реализованы в виде записей или объектов, то атрибуты $X$ могут быть реализованы как поля данных в записях, представляющих узлы $X$. Атрибуты могут быть любого вида: числами, типами, таблицами ссылок или строками. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Дерево разбора, | + | Дерево разбора, в каждом узле которого атрибуты уже вычислены, называется '''аннотированным''' ''(англ. annotated)'', а процесс вычисления этих атрибутов {{---}} '''аннотированием''' дерева разбора. |
}} | }} | ||
{{Определение | {{Определение | ||
| + | |id = tr_char | ||
|definition = | |definition = | ||
| − | '''Транслирующий символ''' {{---}} нетерминал, который раскрывается в $\varepsilon$ и в момент раскрытия выполняет | + | '''Транслирующий символ''' {{---}} нетерминал, который раскрывается в $\varepsilon$ и в момент раскрытия выполняет связанное с ним действие. Действия пишутся в фигурных скобках рядом с транслирующим символом. |
}} | }} | ||
| − | + | Будем рассматривать в качестве примера грамматику для арифметических выражений с операторами $+$ и $*$: | |
| − | $ | + | $ |
| + | S \to E \\ | ||
E \to E + T \mid T \\ | E \to E + T \mid T \\ | ||
| − | T \to T | + | T \to T * F \mid F \\ |
F \to n \mid (E) | F \to n \mid (E) | ||
$ | $ | ||
| − | |||
| − | $ | + | Стоит отметить, что не существует гарантии наличия даже одного порядка обхода дерева разбора, при котором вычислятся все атрибуты в узлах. Рассмотрим для примера следующие нетерминалы $A$ и $B$: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | $ | ||
| + | {| style="background-color:#CCC;margin:0.5px" | ||
| + | !style="background-color:#EEE"| Продукция | ||
| + | !style="background-color:#EEE"| Семантические правила | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| $A \to B$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| $A.s = B.i \\ B.i = A.s+1$ | ||
| + | |} | ||
| + | Данные правила циклические: невозможно вычислить ни $A.s$ в узле, ни $B.i$ в дочернем узле, не зная значение другого атрибута. | ||
| + | Далее будет рассмотрено два класса синтаксически управляемых грамматик, для которых можно однозначно определить порядок вычисления атрибутов. | ||
| − | + | ==Синтезируемые атрибуты== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Атрибут''', значение которого зависит от значений атрибутов | + | '''Атрибут''', значение которого зависит от значений атрибутов детей данного узла или от других атрибутов этого узла, то атрибут называется '''синтезируемым''' ''(англ. synthesized attribute)''. |
}} | }} | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Грамматика называется ''' | + | Грамматика называется '''S-атрибутной''' ''(англ. S-attributed definition)'', если с атрибутами выполняются только операции присваивания значений других атрибутов, а внутри транслирующих символов происходят обращения только к атрибутам этого транслирующего символа. То есть в грамматике используются только синтезируемые атрибуты. Дерево разбора для такой грамматике всегда может быть аннотировано путем выполнения семантических правил снизу вверх, от листьев к корню. |
}} | }} | ||
| + | ===Пример S-атрибутной грамматики=== | ||
| + | Выпишем синтаксически управляемое определение для грамматики арифметических выражений с операторами $+$ и $*$ (здесь $\{ADD {{...}} \}$ и $\{MUL {{...}} \}$ {{---}} [[Атрибутные_транслирующие_грамматики#tr_char|транслирующие символы]]. Если в продукции несколько раз встречается одинаковый нетерминал, будем добавлять к нему индексы, считая от начала продукции.): | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
| − | !style="background-color:#EEE"| | + | !style="background-color:#EEE"| Продукция |
!style="background-color:#EEE"| Семантические правила | !style="background-color:#EEE"| Семантические правила | ||
| + | !style="background-color:#EEE"| Пояснения | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"| $S \to E$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| $S.val=E.val$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 30px"| $ | + | |style="background-color:#FFF;padding:2px 30px"| $E_0 \to E_1 + T\ \{ADD\ res = op_1 + op_2\}$ |
|style="background-color:#FFF;padding:2px 30px"| $ADD.op_1=E_1.val \\ ADD.op_2=T.val \\ E_0.val=ADD.res $ | |style="background-color:#FFF;padding:2px 30px"| $ADD.op_1=E_1.val \\ ADD.op_2=T.val \\ E_0.val=ADD.res $ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| В фигурных скобках {{---}} действия транслирующего символа ADD. $op_1$, $op_2$ и $res$ {{---}} атрибуты транслирующего символа. | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $E \to T$ | |style="background-color:#FFF;padding:2px 30px"| $E \to T$ | ||
|style="background-color:#FFF;padding:2px 30px"| $E.val=T.val$ | |style="background-color:#FFF;padding:2px 30px"| $E.val=T.val$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 30px"| $ | + | |style="background-color:#FFF;padding:2px 30px"| $T_0 \to T_1 * F \ \{MUL\ res = op_1 \times op_2\}$ |
|style="background-color:#FFF;padding:2px 30px"| $MUL.op_1=T.val \\ MUL.op_2=F.val \\ T_0.val=MUL.res$ | |style="background-color:#FFF;padding:2px 30px"| $MUL.op_1=T.val \\ MUL.op_2=F.val \\ T_0.val=MUL.res$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| В фигурных скобках {{---}} действия транслирующего символа MUL. $op_1$, $op_2$ и $res$ {{---}} атрибуты транслирующего символа. | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $T \to F$ | |style="background-color:#FFF;padding:2px 30px"| $T \to F$ | ||
|style="background-color:#FFF;padding:2px 30px"| $T.val=F.val$ | |style="background-color:#FFF;padding:2px 30px"| $T.val=F.val$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $F \to n$ | |style="background-color:#FFF;padding:2px 30px"| $F \to n$ | ||
|style="background-color:#FFF;padding:2px 30px"| $F.val=n.val$ | |style="background-color:#FFF;padding:2px 30px"| $F.val=n.val$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $F \to (E)$ | |style="background-color:#FFF;padding:2px 30px"| $F \to (E)$ | ||
|style="background-color:#FFF;padding:2px 30px"| $F.val=E.val$ | |style="background-color:#FFF;padding:2px 30px"| $F.val=E.val$ | ||
| + | |style="background-color:#FFF;padding:2px 30px"| | ||
|} | |} | ||
| − | + | В нашем примере видно, что $val$ зависит только от детей в дереве разбора, то есть это синтезируемый атрибут. Результат умножителя ($MUL.res$) зависит только от атрибутов атрибутов самого умножителя ($MUL.op_1$ и $MUL.op_2$), а значит тоже является синтезируемым(аналогично с сумматором $ADD$). | |
| + | |||
| + | [[Файл:3mul5add4.png|500px|thumb|center|Аннотированное дерево разбора для '''$3*5+4$''']] | ||
| + | |||
| + | После такого разбора в $S.val$ будет лежать вычисленное значение выражения. Можно, например сразу напечатать его, добавив к нему правило $\{print(S.val)\}$. | ||
| + | |||
| + | ==Наследуемые атрибуты== | ||
| + | |||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Атрибут''', значение которого зависит от значений атрибутов братьев узла или атрибутов родителя, называется '''наследуемым''' ''(англ. inherited attribute)''. | ||
| + | }} | ||
| − | + | {{Определение | |
| − | Для | + | |definition = |
| + | Грамматика называется '''L-атрибутной''' ''(англ. L-attributed definition)'', если значения наследуемых атрибутов зависят только от родителей и братьев слева (то есть не зависят от значений атрибутов братьев справа). | ||
| + | }} | ||
| + | ===Пример L-атрибутной грамматики=== | ||
| + | Для наглядности рассмотрим грамматику объявления переменных | ||
| + | (в начале строки идет тип, затем через запятую имена переменных. Примеры строк, разбираемых в ней: '''int a''' или '''real x,y,z''' и подобные): | ||
| + | $ | ||
| + | D \to TL \\ | ||
| + | T \to int \mid real \\ | ||
| + | L \to L,id \mid id | ||
| + | $ | ||
| − | |||
| − | + | Выпишем продукции (с транслирующими символами) и ассоциируем с ними семантические правила | |
| − | + | (здесь $\{ENTRY {{...}} \}$ {{---}} [[Атрибутные_транслирующие_грамматики#tr_char|транслирующий символ]]. Если в продукции несколько раз встречается одинаковый нетерминал, будем добавлять к нему индексы, считая от начала продукции.): | |
{| style="background-color:#CCC;margin:0.5px" | {| style="background-color:#CCC;margin:0.5px" | ||
| − | !style="background-color:#EEE"| | + | !style="background-color:#EEE"| Продукция |
!style="background-color:#EEE"| Семантические правила | !style="background-color:#EEE"| Семантические правила | ||
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $D \to TL$ | |style="background-color:#FFF;padding:2px 30px"| $D \to TL$ | ||
| − | |style="background-color:#FFF;padding:2px 30px"| $L. | + | |style="background-color:#FFF;padding:2px 30px"| $L.inh = T.type$ |
|- | |- | ||
|style="background-color:#FFF;padding:2px 30px"| $T \to int$ | |style="background-color:#FFF;padding:2px 30px"| $T \to int$ | ||
| Строка 136: | Строка 151: | ||
|style="background-color:#FFF;padding:2px 30px"| $T.type = real$ | |style="background-color:#FFF;padding:2px 30px"| $T.type = real$ | ||
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 30px"| $ | + | |style="background-color:#FFF;padding:2px 30px"| $L_0 \to L_1,id\ \{ENTRY addtype(key, value)\}$ |
| − | |style="background-color:#FFF;padding:2px 30px"| $L_1. | + | |style="background-color:#FFF;padding:2px 30px"| $L_1.inh = L0.inh \\ ENTRY.key=id.text \\ ENTRY.value=L_0.inh$ |
|- | |- | ||
| − | |style="background-color:#FFF;padding:2px 30px"| $L | + | |style="background-color:#FFF;padding:2px 30px"| $L \to id\ \{ENTRY addtype(key, value)\}$ |
| − | |style="background-color:#FFF;padding:2px 30px"| $ENTRY.key=id. | + | |style="background-color:#FFF;padding:2px 30px"| $ENTRY.key=id.text \\ ENTRY.value=L.inh$ |
|} | |} | ||
| − | Семантическое правило $L. | + | Семантическое правило $L.inh = T.type$, связанное с продукцией $D \to TL$, определяет наследуемый атрибут $L.inh$ как тип объявления. Затем приведенные правила распространяют этот тип вниз по дереву разбора с использованием атрибута $L.inh$. Транслирующий символ $ENTRY$, связанный с продукциями для $L$, вызывает процедуру $addtype$ для добавления типа каждого идентификатора к его записи в таблице символов (по ключу, определяемому атрибутом $text$). |
| + | |||
| + | [[Файл:Real_id1,_id2,_id3.png|600px|center|thumb|Аннотированное дерево разбора для '''$\mathbf{real}\ id1,\ id2,\ id3$'''|600px]] | ||
| + | |||
| + | ==Пример работы с атрибутами в нисходящем разборе== | ||
| + | Рассмотрим работы с атрибутами на примере LL(1)-грамматики арифметических выражений, которая уже была разобрана [[Построение FIRST и FOLLOW#Пример | ранее]] и расширим код [[Предиктивный_синтаксический_анализ | разборщика]] для нее: | ||
| + | |||
| + | $ | ||
| + | E \to TE' \\ | ||
| + | E' \to +TE' \mid \varepsilon \\ | ||
| + | T \to FT' \\ | ||
| + | T' \to * FT' \mid \varepsilon \\ | ||
| + | F \to n \mid (E) | ||
| + | $ | ||
| + | |||
| + | В данной реализации рекурсивные функции от нетерминалов получают на вход (если необходимо) наследуемые атрибуты узла и возвращают вершины дерева разбора, в атрибутах которых записан результат вычислений соответствующего подвыражения. Однако этот код легко изменить, чтобы он только вычислял значение выражения и не строил дерево разбора. Как мы видим, $val$ {{---}} синтезируемый атрибут, $acc$ {{---}} наследуемый атрибут, $ADD$ {{---}} транслирующий символ. Синим подсвечены строки, отвечающие за работу с атрибутами. | ||
| + | |||
| + | Здесь <tex>\mathtt{Node}</tex> {{---}} структура следующего вида: | ||
| + | '''struct''' Node | ||
| + | children : '''map<String, Node>''' | ||
| + | name : '''string''' | ||
| + | val : '''int''' <font color="green">// атрибут нетерминала</font> | ||
| + | '''function''' addChild('''Node''') <font color="green">// функция, подвешивающая поддерево к данному узлу</font> | ||
| − | |||
| + | E() : '''Node''' | ||
| + | Node res = Node("E") | ||
| + | '''switch''' (curToken) | ||
| + | '''case''' n, '(' : | ||
| + | res.addChild(T()) <font color="green">// подвешиваем левого сына</font> | ||
| + | <font color="blue">temp = res.children["T"].val</font> <font color="green">// атрибут левого сына</font> | ||
| + | <font color="blue">Node rightSon = E'(temp) </font> <font color="green">// отдадим атрибут левого сына правому как наследуемый атрибут</font> | ||
| + | <font color="blue">res.addChild(rightSon) </font> <font color="green">// подвешиваем правого сына сына</font> | ||
| + | <font color="blue">res.val = res.children["E'"].val</font> | ||
| + | '''break''' | ||
| + | '''default''' : | ||
| + | <font color="red">error</font>("unexpected char") | ||
| + | '''return''' res | ||
| − | + | E'(acc) : '''Node''' | |
| + | Node res = Node("E'") | ||
| + | '''switch''' (curToken) | ||
| + | '''case''' '+' : | ||
| + | consume('+') | ||
| + | res.addChild(Node("+")) | ||
| + | res.addChild(T()) | ||
| + | <font color="blue">temp = res.children["T"].val | ||
| + | ADD.res = ADD(acc, temp) <font color="green">// ADD проведет вычисления из наследуемого атрибута add и атрибута ребенка "T"</font> | ||
| + | res.addChild(E'(ADD.res)) <font color="green">// результат вычислений будет передан правому ребенку как наследуемый атрибут</font> | ||
| + | res.val = res.children["E'"].val</font> | ||
| + | '''break''' | ||
| + | '''case''' '$', ')' : | ||
| + | <font color="blue">res.val = acc</font> | ||
| + | '''break''' | ||
| + | '''default''' : | ||
| + | <font color="red">error</font>("unexpected char") | ||
| + | '''return''' res | ||
| + | F() : '''Node''' | ||
| + | Node res = Node("F") | ||
| + | '''switch''' (curToken) | ||
| + | '''case''' n : | ||
| + | consume(n) | ||
| + | res.addChild(Node(curToken)) | ||
| + | <font color="blue">res.val = n.val</font> | ||
| + | '''break''' | ||
| + | '''case''' '(' : | ||
| + | consume('(') | ||
| + | res.addChild(Node("(")) | ||
| + | res.addChild(E()) | ||
| + | <font color="blue">rev.val = res.children["E"].val</font> | ||
| + | consume(')') | ||
| + | res.addChild(Node(")")) | ||
| + | '''default''' : | ||
| + | <font color="red">error</font>("unexpected char") | ||
| + | '''return''' res | ||
| − | + | Функции для $T$ и $T'$ строятся аналогично. | |
| − | + | [[Файл:2add3add7.png|600px|center|thumb| Дерево разбора для '''$2\ +\ 3\ +\ 7$''']] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Атрибуты в ANTLR== | |
| − | + | Общедоступный генератор разборщиков ANTLR<ref>[http://www.antlr.org/ ANTLR {{---}} Parser generator]</ref> поддерживает синтаксически управляемое определение. | |
| − | |||
| − | + | Рассмотрим для той же грамматики арифметических выражений с операторами <tex>+,\ *</tex>, скобками и выводом результата выражения пример на ANTLR. | |
| − | |||
| − | |||
| − | |||
| − | + | grammar Expression; | |
| + | '''@header''' { package ru.ifmo.ctddev.wiki; } | ||
| − | + | Естественным образом можно добавлять действия в продукции, где это нужно. Действия выполняются после предыдущего элемента грамматики и до следующего. | |
| − | + | Стартовый нетерминал печатает результат: | |
| − | + | s : expr { System.out.println($expr.val); }; | |
| − | |||
| − | |||
| − | $ | ||
| − | < | + | В продукции для нетерминала <code>expr</code> определяется возвращаемое значение (<code>['''int''' val]</code>). Обращение к этому атрибуту имеет вид <code>$expr.value</code>. В фигурных скобках записаны семантические правила. |
| + | Разобранные нетерминалы возвращают результат, вычисленный в поддереве(<code>returns [int val]</code>) как свой синтезируемый атрибут, процесс вычисления которого описан в фигурных скобках <code>{ $val = $exprP.val; }</code>. | ||
| − | + | Наследуемые атрибуты передаются нетерминалу как параметр(<code>exprP[$term.val]</code>). | |
| − | + | expr '''returns''' ['''int''' val] | |
| + | : term exprP[$term.val] { $val = $exprP.val; } | ||
| + | ; | ||
| − | < | + | exprP['''int''' i] '''returns''' ['''int''' val] |
| + | : { $val = $i; } <font color="green"> // <tex>\varepsilon</tex>-правило</font> | ||
| + | | '+' term expr = exprP[$i + $term.val] { $val = $expr.val; } | ||
| + | ; | ||
| + | |||
| + | term '''returns''' ['''int''' val] | ||
| + | : fact termP[$fact.val] { $val = $termP.val; } | ||
| + | ; | ||
| + | termP['''int''' i] '''returns''' '''[int''' val] | ||
| + | : { $val = $i; } | ||
| + | | '*' fact expr = termP[$i * $fact.val] { $val = $expr.val; } | ||
| + | ; | ||
| − | + | fact '''returns''' ['''int''' val] | |
| + | : '(' expr ')' { $val = $expr.val; } | ||
| + | | NUM { $val = Integer.parseInt($NUM.text); } | ||
| + | ; | ||
| + | Техническая деталь для ANTLR, правила для лексического анализатора: | ||
| + | WS : [ \t \r \n]+ -> skip ; | ||
| + | NUM : [0-9]+ ; | ||
| − | </ | + | == Примечания == |
| + | <references/> | ||
== Источники информации == | == Источники информации == | ||
* Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Первое издание. 2003. Стр. 279 {{---}} 305. | * Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Первое издание. 2003. Стр. 279 {{---}} 305. | ||
| − | * Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Второе издание. 2008. Стр. | + | * Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Второе издание. 2008. Стр. 383 {{---}} 398. |
| − | * [https://theantlrguy.atlassian.net/wiki/display/ANTLR4/Parser+Rules#ParserRules | + | * [https://theantlrguy.atlassian.net/wiki/display/ANTLR4/Parser+Rules#ParserRules ANTLR Documentation {{---}} Rule Attribute Definitions] |
| + | * [http://www.amazon.com/The-Definitive-ANTLR-4-Reference/dp/1934356999| The Definitive ANTLR 4 Reference] | ||
[[Категория: Методы трансляции]] | [[Категория: Методы трансляции]] | ||
[[Категория: Нисходящий разбор]] | [[Категория: Нисходящий разбор]] | ||
Текущая версия на 19:15, 4 сентября 2022
Часто, осуществляя разбор, мы хотим извлечь какие-то данные или произвести какие-то действия, а не просто выяснить, разбирается ли текст в данной грамматике. Вообще говоря, сначала можно получить дерево разбора, а потом уже, обходя его, выполнять эти действия. В этом случае происходит дублирование функционала: промежуточное сохранение данных в виде дерева разбора не нужно, а иногда его просто слишком расточительно хранить в памяти целиком. В связи с этим хочется какие-то действия производить уже на этапе разбора.
Например, мы хотим не только построить дерево разбора для арифметических выражений, а ещё и вычислить значение этого выражения. Возможно, даже не строя само дерево разбора.
Такой подход называется синтаксически управляемой трансляцией.
Содержание
Синтаксически управляемая трансляция
| Определение: |
| Синтаксически управляемое определение (англ. syntax-directed definition) является контекстно-свободной грамматикой с атрибутами и правилами. Атрибуты связаны с грамматическими символами, а правила — с продукциями. |
| Определение: |
| Синтаксически управляемая трансляция (англ. syntax-directed translation) — это трансляция, при которой в процессе разбора строки сразу выполняются какие-то действия, без использования промежуточного представления в виде дерева разбора. |
Синтаксически управляемая трансляция вводит две новые сущности: атрибут и транслирующий символ.
| Определение: |
| Атрибут (англ. attribute) — дополнительные данные, ассоциированные с грамматическими символами. Если $X$ представляет собой символ, а $a$ — один из его атрибутов, то значение $a$ в некотором узле дерева разбора, помеченном $X$, записывается как $X.a$. Если узлы дерева разбора реализованы в виде записей или объектов, то атрибуты $X$ могут быть реализованы как поля данных в записях, представляющих узлы $X$. Атрибуты могут быть любого вида: числами, типами, таблицами ссылок или строками. |
| Определение: |
| Дерево разбора, в каждом узле которого атрибуты уже вычислены, называется аннотированным (англ. annotated), а процесс вычисления этих атрибутов — аннотированием дерева разбора. |
| Определение: |
| Транслирующий символ — нетерминал, который раскрывается в $\varepsilon$ и в момент раскрытия выполняет связанное с ним действие. Действия пишутся в фигурных скобках рядом с транслирующим символом. |
Будем рассматривать в качестве примера грамматику для арифметических выражений с операторами $+$ и $*$:
$ S \to E \\ E \to E + T \mid T \\ T \to T * F \mid F \\ F \to n \mid (E) $
Стоит отметить, что не существует гарантии наличия даже одного порядка обхода дерева разбора, при котором вычислятся все атрибуты в узлах. Рассмотрим для примера следующие нетерминалы $A$ и $B$:
| Продукция | Семантические правила |
|---|---|
| $A \to B$ | $A.s = B.i \\ B.i = A.s+1$ |
Данные правила циклические: невозможно вычислить ни $A.s$ в узле, ни $B.i$ в дочернем узле, не зная значение другого атрибута. Далее будет рассмотрено два класса синтаксически управляемых грамматик, для которых можно однозначно определить порядок вычисления атрибутов.
Синтезируемые атрибуты
| Определение: |
| Атрибут, значение которого зависит от значений атрибутов детей данного узла или от других атрибутов этого узла, то атрибут называется синтезируемым (англ. synthesized attribute). |
| Определение: |
| Грамматика называется S-атрибутной (англ. S-attributed definition), если с атрибутами выполняются только операции присваивания значений других атрибутов, а внутри транслирующих символов происходят обращения только к атрибутам этого транслирующего символа. То есть в грамматике используются только синтезируемые атрибуты. Дерево разбора для такой грамматике всегда может быть аннотировано путем выполнения семантических правил снизу вверх, от листьев к корню. |
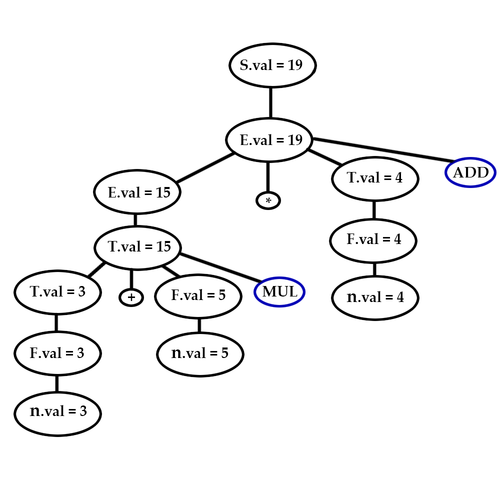
Пример S-атрибутной грамматики
Выпишем синтаксически управляемое определение для грамматики арифметических выражений с операторами $+$ и $*$ (здесь $\{ADD Шаблон:... \}$ и $\{MUL Шаблон:... \}$ — транслирующие символы. Если в продукции несколько раз встречается одинаковый нетерминал, будем добавлять к нему индексы, считая от начала продукции.):
| Продукция | Семантические правила | Пояснения |
|---|---|---|
| $S \to E$ | $S.val=E.val$ | |
| $E_0 \to E_1 + T\ \{ADD\ res = op_1 + op_2\}$ | $ADD.op_1=E_1.val \\ ADD.op_2=T.val \\ E_0.val=ADD.res $ | В фигурных скобках — действия транслирующего символа ADD. $op_1$, $op_2$ и $res$ — атрибуты транслирующего символа. |
| $E \to T$ | $E.val=T.val$ | |
| $T_0 \to T_1 * F \ \{MUL\ res = op_1 \times op_2\}$ | $MUL.op_1=T.val \\ MUL.op_2=F.val \\ T_0.val=MUL.res$ | В фигурных скобках — действия транслирующего символа MUL. $op_1$, $op_2$ и $res$ — атрибуты транслирующего символа. |
| $T \to F$ | $T.val=F.val$ | |
| $F \to n$ | $F.val=n.val$ | |
| $F \to (E)$ | $F.val=E.val$ |
В нашем примере видно, что $val$ зависит только от детей в дереве разбора, то есть это синтезируемый атрибут. Результат умножителя ($MUL.res$) зависит только от атрибутов атрибутов самого умножителя ($MUL.op_1$ и $MUL.op_2$), а значит тоже является синтезируемым(аналогично с сумматором $ADD$).
После такого разбора в $S.val$ будет лежать вычисленное значение выражения. Можно, например сразу напечатать его, добавив к нему правило $\{print(S.val)\}$.
Наследуемые атрибуты
| Определение: |
| Атрибут, значение которого зависит от значений атрибутов братьев узла или атрибутов родителя, называется наследуемым (англ. inherited attribute). |
| Определение: |
| Грамматика называется L-атрибутной (англ. L-attributed definition), если значения наследуемых атрибутов зависят только от родителей и братьев слева (то есть не зависят от значений атрибутов братьев справа). |
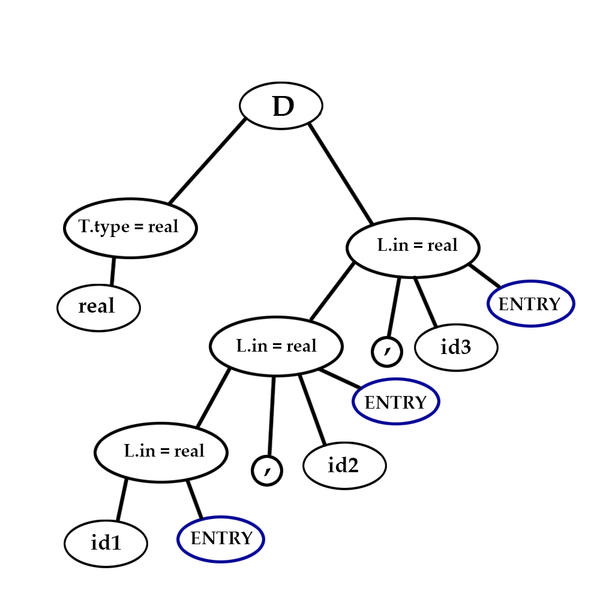
Пример L-атрибутной грамматики
Для наглядности рассмотрим грамматику объявления переменных (в начале строки идет тип, затем через запятую имена переменных. Примеры строк, разбираемых в ней: int a или real x,y,z и подобные):
$ D \to TL \\ T \to int \mid real \\ L \to L,id \mid id $
Выпишем продукции (с транслирующими символами) и ассоциируем с ними семантические правила
(здесь $\{ENTRY Шаблон:... \}$ — транслирующий символ. Если в продукции несколько раз встречается одинаковый нетерминал, будем добавлять к нему индексы, считая от начала продукции.):
| Продукция | Семантические правила |
|---|---|
| $D \to TL$ | $L.inh = T.type$ |
| $T \to int$ | $T.type = integer$ |
| $T \to real$ | $T.type = real$ |
| $L_0 \to L_1,id\ \{ENTRY addtype(key, value)\}$ | $L_1.inh = L0.inh \\ ENTRY.key=id.text \\ ENTRY.value=L_0.inh$ |
| $L \to id\ \{ENTRY addtype(key, value)\}$ | $ENTRY.key=id.text \\ ENTRY.value=L.inh$ |
Семантическое правило $L.inh = T.type$, связанное с продукцией $D \to TL$, определяет наследуемый атрибут $L.inh$ как тип объявления. Затем приведенные правила распространяют этот тип вниз по дереву разбора с использованием атрибута $L.inh$. Транслирующий символ $ENTRY$, связанный с продукциями для $L$, вызывает процедуру $addtype$ для добавления типа каждого идентификатора к его записи в таблице символов (по ключу, определяемому атрибутом $text$).
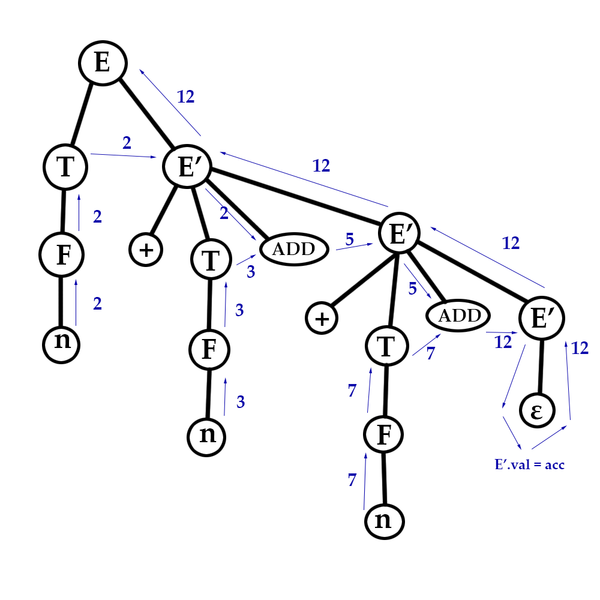
Пример работы с атрибутами в нисходящем разборе
Рассмотрим работы с атрибутами на примере LL(1)-грамматики арифметических выражений, которая уже была разобрана ранее и расширим код разборщика для нее:
$ E \to TE' \\ E' \to +TE' \mid \varepsilon \\ T \to FT' \\ T' \to * FT' \mid \varepsilon \\ F \to n \mid (E) $
В данной реализации рекурсивные функции от нетерминалов получают на вход (если необходимо) наследуемые атрибуты узла и возвращают вершины дерева разбора, в атрибутах которых записан результат вычислений соответствующего подвыражения. Однако этот код легко изменить, чтобы он только вычислял значение выражения и не строил дерево разбора. Как мы видим, $val$ — синтезируемый атрибут, $acc$ — наследуемый атрибут, $ADD$ — транслирующий символ. Синим подсвечены строки, отвечающие за работу с атрибутами.
Здесь — структура следующего вида:
struct Node
children : map<String, Node>
name : string
val : int // атрибут нетерминала
function addChild(Node) // функция, подвешивающая поддерево к данному узлу
E() : Node
Node res = Node("E")
switch (curToken)
case n, '(' :
res.addChild(T()) // подвешиваем левого сына
temp = res.children["T"].val // атрибут левого сына
Node rightSon = E'(temp) // отдадим атрибут левого сына правому как наследуемый атрибут
res.addChild(rightSon) // подвешиваем правого сына сына
res.val = res.children["E'"].val
break
default :
error("unexpected char")
return res
E'(acc) : Node
Node res = Node("E'")
switch (curToken)
case '+' :
consume('+')
res.addChild(Node("+"))
res.addChild(T())
temp = res.children["T"].val
ADD.res = ADD(acc, temp) // ADD проведет вычисления из наследуемого атрибута add и атрибута ребенка "T"
res.addChild(E'(ADD.res)) // результат вычислений будет передан правому ребенку как наследуемый атрибут
res.val = res.children["E'"].val
break
case '$', ')' :
res.val = acc
break
default :
error("unexpected char")
return res
F() : Node
Node res = Node("F")
switch (curToken)
case n :
consume(n)
res.addChild(Node(curToken))
res.val = n.val
break
case '(' :
consume('(')
res.addChild(Node("("))
res.addChild(E())
rev.val = res.children["E"].val
consume(')')
res.addChild(Node(")"))
default :
error("unexpected char")
return res
Функции для $T$ и $T'$ строятся аналогично.
Атрибуты в ANTLR
Общедоступный генератор разборщиков ANTLR[1] поддерживает синтаксически управляемое определение.
Рассмотрим для той же грамматики арифметических выражений с операторами , скобками и выводом результата выражения пример на ANTLR.
grammar Expression;
@header { package ru.ifmo.ctddev.wiki; }
Естественным образом можно добавлять действия в продукции, где это нужно. Действия выполняются после предыдущего элемента грамматики и до следующего.
Стартовый нетерминал печатает результат:
s : expr { System.out.println($expr.val); };
В продукции для нетерминала expr определяется возвращаемое значение ([int val]). Обращение к этому атрибуту имеет вид $expr.value. В фигурных скобках записаны семантические правила.
Разобранные нетерминалы возвращают результат, вычисленный в поддереве(returns [int val]) как свой синтезируемый атрибут, процесс вычисления которого описан в фигурных скобках { $val = $exprP.val; }.
Наследуемые атрибуты передаются нетерминалу как параметр(exprP[$term.val]).
expr returns [int val]
: term exprP[$term.val] { $val = $exprP.val; }
;
exprP[int i] returns [int val]
: { $val = $i; } // -правило
| '+' term expr = exprP[$i + $term.val] { $val = $expr.val; }
;
term returns [int val]
: fact termP[$fact.val] { $val = $termP.val; }
;
termP[int i] returns [int val]
: { $val = $i; }
| '*' fact expr = termP[$i * $fact.val] { $val = $expr.val; }
;
fact returns [int val]
: '(' expr ')' { $val = $expr.val; }
| NUM { $val = Integer.parseInt($NUM.text); }
;
Техническая деталь для ANTLR, правила для лексического анализатора:
WS : [ \t \r \n]+ -> skip ; NUM : [0-9]+ ;
Примечания
Источники информации
- Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Первое издание. 2003. Стр. 279 — 305.
- Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс. Второе издание. 2008. Стр. 383 — 398.
- ANTLR Documentation — Rule Attribute Definitions
- The Definitive ANTLR 4 Reference