Отношение связности, компоненты связности — различия между версиями
(→См. также) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 11 промежуточных версий 8 участников) | |||
| Строка 3: | Строка 3: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Две вершины <tex>u</tex> и <tex>v</tex> называются ''' | + | Две вершины <tex>u</tex> и <tex>v</tex> называются '''связанными''' ''(англ. adjacent)'', если в графе <tex>G</tex> существует [[Основные определения теории графов|путь]] из <tex>u</tex> в <tex>v</tex> (обозначение: <tex>u \rightsquigarrow v </tex>).}} |
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Связность {{---}} '''[[Отношение_эквивалентности|отношение эквивалентности]]''' ''(equivalence relation)''. | + | Связность {{---}} '''[[Отношение_эквивалентности|отношение эквивалентности]]''' ''(англ. equivalence relation)''. |
|proof= | |proof= | ||
'''[[Рефлексивное_отношение|Рефлексивность]]''': <tex>\forall a \in V a \rightsquigarrow a</tex> (очевидно). | '''[[Рефлексивное_отношение|Рефлексивность]]''': <tex>\forall a \in V a \rightsquigarrow a</tex> (очевидно). | ||
| Строка 19: | Строка 19: | ||
|id = def2 | |id = def2 | ||
|definition= | |definition= | ||
| − | '''Компонентой связности''' ''(connected component)'' называется класс эквивалентности относительно связности.}} | + | '''Компонентой связности''' ''(англ. connected component)'' называется класс эквивалентности относительно связности.}} |
{{Определение | {{Определение | ||
|id = connected_graph | |id = connected_graph | ||
|definition= | |definition= | ||
| − | Граф <tex>G=(V, E)</tex> называется '''связным''' ''(connectivity graph)'', если он состоит из одной компоненты связности. В противном случае граф называется '''несвязным'''.}} | + | Граф <tex>G=(V, E)</tex> называется '''связным''' ''(англ. connectivity graph)'', если он состоит из одной компоненты связности. В противном случае граф называется '''несвязным'''.}} |
== Случай ориентированного графа == | == Случай ориентированного графа == | ||
В общем случае для ориентированного графа существование пути — не симметричное отношение, поэтому вместо понятия связности различают понятие слабой и сильной связности. | В общем случае для ориентированного графа существование пути — не симметричное отношение, поэтому вместо понятия связности различают понятие слабой и сильной связности. | ||
=== Слабая связность === | === Слабая связность === | ||
| − | + | {{Определение | |
|definition= | |definition= | ||
| − | Отношение $R(v, u)$ называется отношением '''слабой связности''' ''(weak connectivity)'', если вершины $u$ и $v$ связаны в неориентированном графе $G'$, полученном из графа $G$ удалением ориентации с рёбер. | + | Отношение $R(v, u)$ называется отношением '''слабой связности''' ''(англ. weak connectivity)'', если вершины $u$ и $v$ связаны в неориентированном графе $G'$, полученном из графа $G$ удалением ориентации с рёбер. |
}} | }} | ||
| Строка 42: | Строка 42: | ||
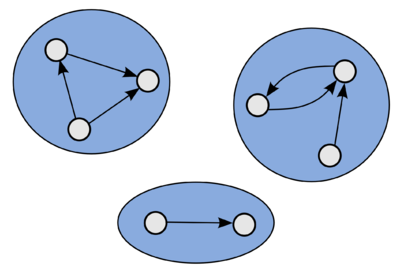
[[Файл:components1.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами слабой связности.]] | [[Файл:components1.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами слабой связности.]] | ||
<br clear="all" /> | <br clear="all" /> | ||
| − | |||
=== Сильная связность === | === Сильная связность === | ||
| Строка 48: | Строка 47: | ||
|id=sc_def | |id=sc_def | ||
|definition= | |definition= | ||
| − | Отношение <tex>R(v, u) = v \rightsquigarrow u \land u \rightsquigarrow v</tex> на вершинах графа называется отношением '''сильной связности''' ''(strong connectivity)''. | + | Отношение <tex>R(v, u) = v \rightsquigarrow u \land u \rightsquigarrow v</tex> на вершинах графа называется отношением '''сильной связности''' ''(англ. strong connectivity)''. |
}} | }} | ||
| Строка 61: | Строка 60: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Пусть <tex>G = (V, E)</tex> — [[Основные_определения_теории_графов|ориентированный граф]]. '''Компонентой сильной связности''' ''(strongly connected component)'' называется класс эквивалентности множества вершин этого графа относительно сильной связности.}} | + | Пусть <tex>G = (V, E)</tex> — [[Основные_определения_теории_графов|ориентированный граф]]. '''Компонентой сильной связности''' ''(англ. strongly connected component)'' называется класс эквивалентности множества вершин этого графа относительно сильной связности.}} |
| + | Компоненты сильной связности могут быть найдены [[Использование обхода в глубину для поиска компонент сильной связности|с помощью обхода в глубину]]. | ||
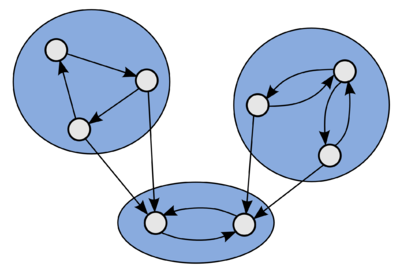
[[Файл:Components2.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами сильной связности.]] | [[Файл:Components2.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами сильной связности.]] | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | [[Основные_определения_теории_графов|Ориентированный граф]] <tex>G = (V, E)</tex> называется '''сильно связным''' ''(strongly connected)'', если он состоит из одной компоненты сильной связности.}} | + | [[Основные_определения_теории_графов|Ориентированный граф]] <tex>G = (V, E)</tex> называется '''сильно связным''' ''(англ. strongly connected)'', если он состоит из одной компоненты сильной связности.}} |
<br clear="all" /> | <br clear="all" /> | ||
| Строка 71: | Строка 71: | ||
==См. также== | ==См. также== | ||
| − | *[[ | + | *[[Отношение рёберной двусвязности]] |
| − | *[[ | + | *[[Отношение вершинной двусвязности]] |
==Источники информации== | ==Источники информации== | ||
Текущая версия на 19:30, 4 сентября 2022
Случай неориентированного графа
| Определение: |
| Две вершины и называются связанными (англ. adjacent), если в графе существует путь из в (обозначение: ). |
| Теорема: |
Связность — отношение эквивалентности (англ. equivalence relation). |
| Доказательство: |
|
Рефлексивность: (очевидно). Симметричность: (в силу неориентированности графа). Транзитивность: . Действительно, сначала пройдем от до , затем от до , что и означает существования пути . |
| Определение: |
| Компонентой связности (англ. connected component) называется класс эквивалентности относительно связности. |
| Определение: |
| Граф называется связным (англ. connectivity graph), если он состоит из одной компоненты связности. В противном случае граф называется несвязным. |
Случай ориентированного графа
В общем случае для ориентированного графа существование пути — не симметричное отношение, поэтому вместо понятия связности различают понятие слабой и сильной связности.
Слабая связность
| Определение: |
| Отношение $R(v, u)$ называется отношением слабой связности (англ. weak connectivity), если вершины $u$ и $v$ связаны в неориентированном графе $G'$, полученном из графа $G$ удалением ориентации с рёбер. |
| Теорема: |
Слабая связность является отношением эквивалентности. |
| Доказательство: |
| Аналогично доказательству соответствующей теоремы для неориентированного графа. |
Сильная связность
| Определение: |
| Отношение на вершинах графа называется отношением сильной связности (англ. strong connectivity). |
| Теорема: |
Сильная связность — отношение эквивалентности. |
| Доказательство: |
|
Рефлексивность и симметричность очевидны. Рассмотрим транзитивность: |
| Определение: |
| Пусть — ориентированный граф. Компонентой сильной связности (англ. strongly connected component) называется класс эквивалентности множества вершин этого графа относительно сильной связности. |
Компоненты сильной связности могут быть найдены с помощью обхода в глубину.
| Определение: |
| Ориентированный граф называется сильно связным (англ. strongly connected), если он состоит из одной компоненты сильной связности. |
См. также
Источники информации
- Отношения связности для вершин неорграфа на ivtb.ru
- Харари Фрэнк Теория графов: Пер. с англ./ Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 296 с. — ISBN 978-5-397-00622-4.