Pintreepi1Lmax — различия между версиями
Zernov (обсуждение | вклад) (→Второй шаг) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 53 промежуточные версии 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | <tex dpi = "200">P \mid | + | <tex dpi = "200">P \mid intree, p_{i} = 1 \mid L_{max}</tex> |
{{Задача | {{Задача | ||
|definition=Рассмотрим задачу на нахождение расписания: | |definition=Рассмотрим задачу на нахождение расписания: | ||
# У нас есть несколько станков, работающих параллельно. У станков могут быть разные скорости выполнения работ. | # У нас есть несколько станков, работающих параллельно. У станков могут быть разные скорости выполнения работ. | ||
| − | # Есть несколько заданий, каждое из которых имеет определенный порядок, который указан в направленном из корней в лист intree- | + | # Есть несколько заданий, каждое из которых имеет определенный порядок, который указан в направленном из корней в лист [[Классификация задач#intree|intree-дерева]], которое имеет несколько корней и один лист. |
# Любая работа на любом станке выполняется единицу времени. | # Любая работа на любом станке выполняется единицу времени. | ||
| − | Требуется минимизировать максимальное опоздание <tex>L_{max} = \max\limits_i \{C_i - d_i\}</tex> | + | Требуется минимизировать максимальное опоздание <tex>L_{max} = \max\limits_i \{C_i - d_i\}</tex>. |
}} | }} | ||
== Описание алгоритма == | == Описание алгоритма == | ||
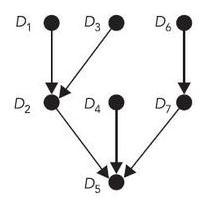
| − | [[Файл:Intree_example.jpg|thumb|Right|Пример | + | [[Файл:Intree_example.jpg|thumb|Right|Пример intree-дерева]] |
=== Идея === | === Идея === | ||
| − | Все | + | Все работы хранятся в качестве вершин [[Классификация задач#intree|intree-дерева]], состоящем из <tex>n</tex> вершин. В intree-дереве у одной вершины может быть два и более родителей. |
| + | Решение задачи состоит из двух шагов: | ||
| − | + | # Меняем делайны работ в соответствии с их очередностью: для всех <tex>i, j</tex> таких, что существует ребро из <tex>i</tex> в <tex>j</tex> будем менять <tex>{d_i}</tex> на <tex>\min ({d_i}, {d_j} - 1) </tex>. | |
| − | + | # Работы расставляются в неубывающем порядке их дедлайнов. | |
| − | На первом шаге | + | === Псевдокод === |
| + | ==== Первый шаг ==== | ||
| + | На первом шаге мы релаксируем дедлайны всех работ, кроме листовой, в соответствии с предыдущим пунктом. | ||
| + | * В массиве <tex>\mathtt d</tex> хранятся дедлайны работ. | ||
| + | * В массиве <tex>\mathtt {parents}</tex> {{---}} массив предков <tex>i</tex>-й работы. | ||
| + | * В переменной <tex>\mathtt i</tex> хранится номер листа (он один, см. условие задачи). | ||
| + | '''Deque<int>''' deque = <tex>\varnothing</tex> | ||
| + | deque.push(i) | ||
| + | '''while''' '''not''' deque.isEmpty | ||
| + | '''int''' j = deque.removeFirst() | ||
| + | '''for''' k '''in''' parents[j] | ||
| + | d[k] = min(d[k], d[j] - 1) | ||
| + | deque.addLast(k) | ||
| − | === | + | ==== Второй шаг ==== |
| − | + | На втором этапе алгоритма работы сортируются в неубывающем порядке их дедлайнов. Предполагается, что работы будут занумерованы так, что <tex>d_{i} \leqslant d_{j}</tex>, если <tex>i \leqslant j</tex>. | |
| − | + | * В переменной <tex>\mathtt F</tex> хранится время, когда какой-либо станок освободится. | |
| − | + | * В массиве <tex>\mathtt r</tex> хранится информация о максимальном времени завершении обработки родителя. | |
| − | + | * Массив <tex>\mathtt q</tex> хранит информацию о количестве работ, готовых к исполнению (находящихся в очереди) в момент времени <tex>t</tex>. | |
| − | + | * Массив <tex>\mathtt x</tex> хранит информацию о начале выполнения работы <tex>i</tex>. | |
| − | + | * В массиве <tex>\mathtt {child}</tex> хранится индекс ребенка <tex>i</tex>-й работы. | |
| − | + | ||
| − | + | F = 0 | |
| + | '''for''' '''int''' i = 1 .. n | ||
| + | r[i] = 0 | ||
| + | '''for''' '''int''' t = 0 .. n | ||
| + | q[t] = 0 | ||
| + | '''for''' '''int''' i = 1 .. n | ||
| + | '''int''' t = max(r[i], F) | ||
| + | x[i] = t | ||
| + | q[t] = q[t] + 1 | ||
| + | '''if''' q[t] == m | ||
| + | F = t + 1 | ||
| + | '''int''' j = child[i] | ||
| + | r[j] = max(r[j], t + 1) | ||
| + | |||
| + | В результате ответ можно получить, зная конечный массив <tex>\mathtt x</tex> и делайны работ: <tex>L_{max} = \max\limits_i (\mathtt x[i] + 1 - d_{i}</tex>), так как все работы выполняются единицу времени, следовательно, <tex>C_{i} = \mathtt x[i] + 1</tex>. Можно заметить, что при вычислении ответа неважно, какие дедлайны использовать, начальные или релаксированные, потому что для любого <tex>k</tex> и его предка <tex>i</tex> либо производится релаксация и выполняется равенство <tex> d_{k} = d_{i} - 1</tex>, а значит, после релаксации максимум не изменится, поскольку при замене дедлайна на меньший максимум увеличится, а новое значение <tex>L_{k}</tex> будет равно <tex>L_{i}</tex>, либо мы не делали релаксацию, и значение <tex>d_{k}</tex>, и, следовательно, <tex>L_{k}</tex> не поменяются. | ||
| + | |||
| + | === Доказательство корректности === | ||
| + | ==== Первый шаг ==== | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
Работа с новым сроком <tex>{d'_i}</tex> в расписании не имеет опозданий тогда и только тогда, когда она не имела опозданий с оригинальным сроком <tex>{d_i}</tex>. | Работа с новым сроком <tex>{d'_i}</tex> в расписании не имеет опозданий тогда и только тогда, когда она не имела опозданий с оригинальным сроком <tex>{d_i}</tex>. | ||
|proof= | |proof= | ||
| − | <tex>\Rightarrow </tex>: Т.к. <tex>{d'_i} \leqslant {d_i}</tex>, значит, если опозданий не было со значениями <tex>{d'_i}</tex>, их не будет и со значениями <tex>{d_i}</tex>. | + | <tex>\Rightarrow </tex> |
| + | :Т.к. <tex>{d'_i} \leqslant {d_i}</tex>, значит, если опозданий не было со значениями <tex>{d'_i}</tex>, их не будет и со значениями <tex>{d_i}</tex>. | ||
| − | <tex>\Leftarrow </tex>: Пусть у нас были сроки <tex>{d_i}</tex> и мы их заменили на <tex>{d'_i}</tex> в соответствии с приведенным алгоритмом. | + | <tex>\Leftarrow </tex> |
| − | :Пронумеруем вершины от <tex>1</tex> до <tex>n</tex> в соответствии с '''обратным''' порядком обхода в алгоритме изменения сроков. В соответствии с расписанием, время, когда деталь закончит обрабатываться на станке <tex>{C_i}</tex> удовлетворяет неравенству <tex>{C_i} \leqslant {d_i}</tex> для всех <tex>{C_1} \dots {C_n}</tex>. Тогда мы имеем <tex>{C_n} \leqslant {d_n} = {d'_n}</tex>. Если для какого-то <tex>1 < r \leqslant n</tex> мы имеем <tex>{C_n} \leqslant {d'_n}</tex> для <tex>i = r \dots n </tex> и существует работа <tex>j</tex> из этого промежутка, что вершина с номером <tex>r - 1</tex> является ее родителем, тогда <tex>C_{r-1} \leqslant \min(d_{r-1},d'_{j}-1) = d'_{r-1}</tex> | + | :Пусть у нас были сроки <tex>{d_i}</tex> и мы их заменили на <tex>{d'_i}</tex> в соответствии с приведенным алгоритмом. |
| + | :Пронумеруем вершины от <tex>1</tex> до <tex>n</tex> в соответствии с '''обратным''' порядком обхода в алгоритме изменения сроков, причём <tex>d_{i} \leqslant d_{j}</tex>, если <tex>i \leqslant j</tex>. В соответствии с расписанием, время, когда деталь закончит обрабатываться на станке <tex>{C_i}</tex> удовлетворяет неравенству <tex>{C_i} \leqslant {d_i}</tex> для всех <tex>{C_1} \dots {C_n}</tex>. Тогда мы имеем <tex>{C_n} \leqslant {d_n} = {d'_n}</tex>. Если для какого-то <tex>1 < r \leqslant n</tex> мы имеем <tex>{C_n} \leqslant {d'_n}</tex> для <tex>i = r \dots n </tex> и существует работа <tex>j</tex> из этого промежутка, что вершина с номером <tex>r - 1</tex> является ее родителем, тогда <tex>C_{r-1} \leqslant \min(d_{r-1},d'_{j}-1) = d'_{r-1}</tex>. | ||
}} | }} | ||
| − | === Второй шаг === | + | ==== Второй шаг ==== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Расписание, сгенерированное этим алгоритмом имеет важное свойство: число заданий в очереди в любой момент времени <tex>t</tex> меньше, чем в момент <tex>t + 1</tex>. Действительно, пусть во время <tex>t</tex> мы выполняем <tex>k</tex> работ, и хотя бы <tex>k + 1 \leqslant m</tex> работ готовы к выполению в момент времени <tex>t + 1</tex>. Но т.к. <tex>k + 1 \leqslant m</tex>, значит каждой из работ предшествовала как минимум одна, поскольку у всех вершин, кроме корней, есть как минимум один предок. Значит, в момент времени <tex>t</tex> исполнялось не менее <tex>k + 1</tex> работ, противоречие. | Расписание, сгенерированное этим алгоритмом имеет важное свойство: число заданий в очереди в любой момент времени <tex>t</tex> меньше, чем в момент <tex>t + 1</tex>. Действительно, пусть во время <tex>t</tex> мы выполняем <tex>k</tex> работ, и хотя бы <tex>k + 1 \leqslant m</tex> работ готовы к выполению в момент времени <tex>t + 1</tex>. Но т.к. <tex>k + 1 \leqslant m</tex>, значит каждой из работ предшествовала как минимум одна, поскольку у всех вершин, кроме корней, есть как минимум один предок. Значит, в момент времени <tex>t</tex> исполнялось не менее <tex>k + 1</tex> работ, противоречие. | ||
| Строка 70: | Строка 78: | ||
Если существует такое расписание, в котором ни одна из работ не будет выполнена с опозданием, то тогда это свойство сохранится в построенном данным алгоритмом расписании | Если существует такое расписание, в котором ни одна из работ не будет выполнена с опозданием, то тогда это свойство сохранится в построенном данным алгоритмом расписании | ||
|proof= | |proof= | ||
| − | Предположим, что существует работа из <tex>x_{1} \dots x_{n}</tex> расписания, построенного алгоритмом. В таком случае существует работа, которая опоздала по отношению к измененным срокам. Возьмем наименьшее <tex>i</tex> такое, что <tex>x(i) + 1 > d'_{i}</tex>. Пусть <tex>t < d'_{i}</tex> {{---}} наибольшее из удовлетворяющих условию <tex>j < m | + | Предположим, что существует работа из <tex>x_{1} \dots x_{n}</tex> расписания, построенного алгоритмом. В таком случае существует работа, которая опоздала по отношению к измененным срокам. Возьмем наименьшее <tex>i</tex> такое, что <tex>x(i) + 1 > d'_{i}</tex>. Пусть <tex>t < d'_{i}</tex> {{---}} наибольшее из удовлетворяющих условию <tex>j < m </tex>, где <tex> x(j) = t, d'_{j} \leqslant d'_{i}</tex> |
Такое <tex>t</tex> существует, потому что иначе <tex>m \cdot d'_{i}</tex> работ <tex>j</tex> с <tex>d'_{j} \leqslant d'_{i}</tex> находятся в очереди до <tex>d'_{i}</tex>. Работа <tex>i</tex> к ним не принадлежит, поскольку <tex>x(i) + 1 > d'_{i}</tex>, а значит, что <tex>m \cdot d'_{i} + 1</tex> должны быть в очереди в момент времени <tex>0 \dots d'_{i}</tex> и ни одна работа не должна опаздывать. Противоречие. | Такое <tex>t</tex> существует, потому что иначе <tex>m \cdot d'_{i}</tex> работ <tex>j</tex> с <tex>d'_{j} \leqslant d'_{i}</tex> находятся в очереди до <tex>d'_{i}</tex>. Работа <tex>i</tex> к ним не принадлежит, поскольку <tex>x(i) + 1 > d'_{i}</tex>, а значит, что <tex>m \cdot d'_{i} + 1</tex> должны быть в очереди в момент времени <tex>0 \dots d'_{i}</tex> и ни одна работа не должна опаздывать. Противоречие. | ||
Любая работа <tex>j</tex> с <tex>d'_{j} \leqslant d'_{i} </tex> и <tex> x(j) > t </tex> должна иметь предка, начавшего работать в момент времени <tex>t</tex>. Теперь рассмотрим два случая: | Любая работа <tex>j</tex> с <tex>d'_{j} \leqslant d'_{i} </tex> и <tex> x(j) > t </tex> должна иметь предка, начавшего работать в момент времени <tex>t</tex>. Теперь рассмотрим два случая: | ||
| Строка 83: | Строка 91: | ||
}} | }} | ||
| + | ==== Корректность алгоритма ==== | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Данный алгоритм корректно решает задачу <tex>P \mid | + | Данный алгоритм корректно решает задачу <tex>P \mid intree, p_{i} = 1 \mid L_{max}</tex> |
|proof= | |proof= | ||
Пусть <tex>L'_{max}</tex> {{---}} оптимальное значение. В таком случае, существует расписание, удовлетворяющее <tex>\max\limits_i \{C_i - d_i\} \leqslant L'_{max}</tex>, что эквивалетно выражению <tex>C_{i} \leqslant d_{i} + L'_{max}</tex> для <tex>i = 1 \dots n </tex>. По первой лемме расписание <tex>S</tex>, построенное для сдвинутых дат <tex>d_{i} + L'_{max}</tex> удовлетворяет данным выражениям. Таким образом, оно оптимально. Нетрудно заметить, что <tex>S</tex> идентично расписанию, построенному алгоритмом, т.к. <tex>(d_{i}+L'_{max})' = d'_{i} + L'_{max} </tex> для <tex>i = 1 \dots n </tex> | Пусть <tex>L'_{max}</tex> {{---}} оптимальное значение. В таком случае, существует расписание, удовлетворяющее <tex>\max\limits_i \{C_i - d_i\} \leqslant L'_{max}</tex>, что эквивалетно выражению <tex>C_{i} \leqslant d_{i} + L'_{max}</tex> для <tex>i = 1 \dots n </tex>. По первой лемме расписание <tex>S</tex>, построенное для сдвинутых дат <tex>d_{i} + L'_{max}</tex> удовлетворяет данным выражениям. Таким образом, оно оптимально. Нетрудно заметить, что <tex>S</tex> идентично расписанию, построенному алгоритмом, т.к. <tex>(d_{i}+L'_{max})' = d'_{i} + L'_{max} </tex> для <tex>i = 1 \dots n </tex> | ||
}} | }} | ||
| + | |||
| + | ==== Асимптотика ==== | ||
| + | # На первом шаге мы посещаем каждую вершину не более двух раз (первый {{---}} когда ищем вершину без родителя, второй {{---}} когда релаксируем дедлайны) за <tex>O(n)</tex> времени. | ||
| + | # Делаем сортировку вершин за <tex>O(n \log n)</tex>, а затем обходим все вершины по разу и считаем время начала выполнения каждой работы, в сумме за <tex>O(n)</tex>. | ||
| + | Итоговая сложность {{---}} <tex>O(n \log n)</tex> | ||
| + | |||
| + | ==См. также== | ||
| + | *[[P2precpi1Lmax|<tex>P2 \mid prec, p_i = 1 \mid L_{\max}</tex>]] | ||
| + | *[[1outtreesumwc | <tex>1 \mid outtree \mid \sum w_i C_i</tex>]] | ||
==Источники информации== | ==Источники информации== | ||
Текущая версия на 19:26, 4 сентября 2022
| Задача: |
Рассмотрим задачу на нахождение расписания:
|
Описание алгоритма
Идея
Все работы хранятся в качестве вершин intree-дерева, состоящем из вершин. В intree-дереве у одной вершины может быть два и более родителей. Решение задачи состоит из двух шагов:
- Меняем делайны работ в соответствии с их очередностью: для всех таких, что существует ребро из в будем менять на .
- Работы расставляются в неубывающем порядке их дедлайнов.
Псевдокод
Первый шаг
На первом шаге мы релаксируем дедлайны всех работ, кроме листовой, в соответствии с предыдущим пунктом.
- В массиве хранятся дедлайны работ.
- В массиве — массив предков -й работы.
- В переменной хранится номер листа (он один, см. условие задачи).
Deque<int> deque =
deque.push(i)
while not deque.isEmpty
int j = deque.removeFirst()
for k in parents[j]
d[k] = min(d[k], d[j] - 1)
deque.addLast(k)
Второй шаг
На втором этапе алгоритма работы сортируются в неубывающем порядке их дедлайнов. Предполагается, что работы будут занумерованы так, что , если .
- В переменной хранится время, когда какой-либо станок освободится.
- В массиве хранится информация о максимальном времени завершении обработки родителя.
- Массив хранит информацию о количестве работ, готовых к исполнению (находящихся в очереди) в момент времени .
- Массив хранит информацию о начале выполнения работы .
- В массиве хранится индекс ребенка -й работы.
F = 0
for int i = 1 .. n
r[i] = 0
for int t = 0 .. n
q[t] = 0
for int i = 1 .. n
int t = max(r[i], F)
x[i] = t
q[t] = q[t] + 1
if q[t] == m
F = t + 1
int j = child[i]
r[j] = max(r[j], t + 1)
В результате ответ можно получить, зная конечный массив и делайны работ: ), так как все работы выполняются единицу времени, следовательно, . Можно заметить, что при вычислении ответа неважно, какие дедлайны использовать, начальные или релаксированные, потому что для любого и его предка либо производится релаксация и выполняется равенство , а значит, после релаксации максимум не изменится, поскольку при замене дедлайна на меньший максимум увеличится, а новое значение будет равно , либо мы не делали релаксацию, и значение , и, следовательно, не поменяются.
Доказательство корректности
Первый шаг
| Лемма: |
Работа с новым сроком в расписании не имеет опозданий тогда и только тогда, когда она не имела опозданий с оригинальным сроком . |
| Доказательство: |
|
|
Второй шаг
Расписание, сгенерированное этим алгоритмом имеет важное свойство: число заданий в очереди в любой момент времени меньше, чем в момент . Действительно, пусть во время мы выполняем работ, и хотя бы работ готовы к выполению в момент времени . Но т.к. , значит каждой из работ предшествовала как минимум одна, поскольку у всех вершин, кроме корней, есть как минимум один предок. Значит, в момент времени исполнялось не менее работ, противоречие.
| Лемма: |
Если существует такое расписание, в котором ни одна из работ не будет выполнена с опозданием, то тогда это свойство сохранится в построенном данным алгоритмом расписании |
| Доказательство: |
|
Предположим, что существует работа из расписания, построенного алгоритмом. В таком случае существует работа, которая опоздала по отношению к измененным срокам. Возьмем наименьшее такое, что . Пусть — наибольшее из удовлетворяющих условию , где Такое существует, потому что иначе работ с находятся в очереди до . Работа к ним не принадлежит, поскольку , а значит, что должны быть в очереди в момент времени и ни одна работа не должна опаздывать. Противоречие. Любая работа с и должна иметь предка, начавшего работать в момент времени . Теперь рассмотрим два случая: Первый случай: .
Второй случай: .
|
Корректность алгоритма
| Теорема: |
Данный алгоритм корректно решает задачу |
| Доказательство: |
| Пусть — оптимальное значение. В таком случае, существует расписание, удовлетворяющее , что эквивалетно выражению для . По первой лемме расписание , построенное для сдвинутых дат удовлетворяет данным выражениям. Таким образом, оно оптимально. Нетрудно заметить, что идентично расписанию, построенному алгоритмом, т.к. для |
Асимптотика
- На первом шаге мы посещаем каждую вершину не более двух раз (первый — когда ищем вершину без родителя, второй — когда релаксируем дедлайны) за времени.
- Делаем сортировку вершин за , а затем обходим все вершины по разу и считаем время начала выполнения каждой работы, в сумме за .
Итоговая сложность —
См. также
Источники информации
- Peter Brucker «Scheduling Algorithms», fifth edition, Springer — с. 151-156 ISBN 978-3-540-69515-8