Алгоритм Куна для поиска максимального паросочетания — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показана 71 промежуточная версия 10 участников) | |||
| Строка 1: | Строка 1: | ||
| + | ==Теорема== | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Если из вершины <tex>x</tex> не существует дополняющей цепи относительно паросочетания <tex>M</tex> | + | Если из вершины <tex>x</tex> не существует [[Теорема о максимальном паросочетании и дополняющих цепях|дополняющей цепи]] относительно паросочетания <tex>M</tex> и паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи, тогда из <tex>x</tex> не существует дополняющей цепи в <tex>M'</tex>. |
| − | |proof=Доказательство от противного | + | |proof= |
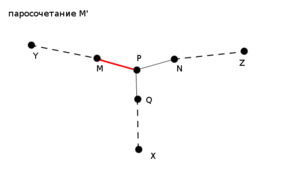
| + | [[Файл:Kuhn2.png|thumb|right|300x300px|Рисунок 1.]] | ||
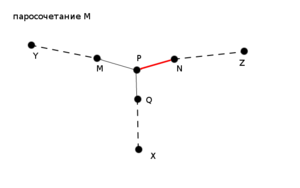
| + | [[Файл:Kuhn1.png|thumb|right|300x300px|Рисунок 2.<br>Пунктиром обозначен путь между двумя вершинами. Ребро красного цвета лежит в паросочетании, а черного - нет.]] | ||
| + | : Доказательство от противного.<br><br> | ||
| + | : Допустим в паросочетание внесли изменения вдоль дополняющей цепи <tex>(y \rightsquigarrow z)</tex> и из вершины <tex>x</tex> появилась дополняющая цепь. | ||
| + | : Заметим, что эта дополняющая цепь должна вершинно пересекаться с той цепью, вдоль которой вносились изменения, иначе такая же дополняющая цепь из <tex>x</tex> существовала и в исходном паросочетании.<br><br> | ||
| + | : Пусть <tex>p</tex> – ближайшая к <tex>x</tex> вершина, которая принадлежит и новой дополняющей цепи и цепи <tex>(y \rightsquigarrow z)</tex>. | ||
| + | : Тогда <tex>MP</tex> – последнее ребро на отрезке <tex>(y \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>NP</tex> – последнее ребро на отрезке <tex>(z \rightsquigarrow p)</tex> цепи <tex>(y \rightsquigarrow z)</tex>, <tex>QP</tex> - последнее ребро лежащее на отрезке <tex>(x \rightsquigarrow p)</tex> новой дополняющей цепи(см. Рисунок 1).<br><br> | ||
| + | : Допустим <tex>MP</tex> принадлежит паросочетанию <tex>M'</tex>, тогда <tex>NP</tex> ему не принадлежит.<br> | ||
| + | :: (Случай, когда <tex>NP</tex> принадлежит паросочетанию <tex>M'</tex> полностью симметричен.)<br><br> | ||
| + | : Поскольку паросочетание <tex>M'</tex> получается из <tex>M</tex> изменением вдоль дополняющей цепи <tex>(y \rightsquigarrow z)</tex>, в паросочетание <tex>M</tex> входило ребро <tex>NP</tex>, а ребро <tex>MP</tex> нет. | ||
| + | : Кроме того, ребро <tex>QP</tex> не лежит ни в исходном паросочетании <tex>M</tex>, ни в паросочетании <tex>M'</tex>, в противном случае оказалось бы, что вершина <tex>p</tex> инцидентна нескольким рёбрам из паросочетания, что противоречит определению паросочетания.<br><br> | ||
| + | :Тогда заметим, что цепь <tex>(x \rightsquigarrow z)</tex>, полученная объединением цепей <tex>(x \rightsquigarrow p)</tex> и <tex>(p \rightsquigarrow z)</tex>, по определению будет дополняющей в паросочетании <tex>M</tex>, что приводит к противоречию, поскольку в паросочетании <tex>M</tex> из вершины <tex>x</tex> не существует дополняющей цепи. | ||
}} | }} | ||
| + | |||
==Алгоритм== | ==Алгоритм== | ||
| − | + | Задан граф <tex>G\langle V, E \rangle</tex>, про который известно, что он двудольный, но разбиение не задано явно. Требуется найти наибольшее паросочетание в нём | |
| − | 1) | + | |
| + | Алгоритм можно описать так: сначала возьмём пустое паросочетание, а потом — пока в графе удаётся найти увеличивающую цепь, — будем выполнять чередование паросочетания вдоль этой цепи, и повторять процесс поиска увеличивающей цепи. Как только такую цепь найти не удалось — процесс останавливаем, — текущее паросочетание и есть максимальное. | ||
| + | |||
| + | В массиве <tex>\mathtt{matching}</tex> хранятся паросочетания <tex> (v, \mathtt{matching}[v]) </tex> (Если паросочетания с вершиной <tex> v </tex> не существует, то <tex> \mathtt{matching}[v]= -1</tex>). А <tex>used</tex> — обычный массив "посещённостей" вершин в обходе в глубину (он нужен, чтобы обход в глубину не заходил в одну вершину дважды). | ||
| + | Функция <tex> \mathrm{dfs} </tex> возвращает <tex>true</tex>, если ей удалось найти увеличивающую цепь из вершины <tex>v</tex>, при этом считается, что эта функция уже произвела чередование паросочетания вдоль найденной цепи. | ||
| + | |||
| + | Внутри функции просматриваются все рёбра, исходящие из вершины <tex>v</tex>, и затем проверяется: если это ребро ведёт в ненасыщенную вершину <tex> to</tex>, либо если эта вершина <tex>to</tex> насыщена, но удаётся найти увеличивающую цепь рекурсивным запуском из <tex>\mathtt{matching}[to]</tex>, то мы говорим, что мы нашли увеличивающую цепь, и перед возвратом из функции с результатом <tex>true</tex> производим чередование в текущем ребре: перенаправляем ребро, смежное с <tex>to</tex>, в вершину <tex> v</tex>. | ||
| + | |||
| + | В основной программе сначала указывается, что текущее паросочетание — пустое (массив <tex> \mathtt{matching}</tex> заполняется числами <tex>-1</tex>). Затем перебирается вершина <tex>v </tex>, и из неё запускается обход в глубину <tex> \mathrm{dfs} </tex>, предварительно обнулив массив <tex> used</tex>. | ||
| + | |||
| + | Стоит заметить, что размер паросочетания легко получить как число вызовов <tex> \mathrm{dfs} </tex> в основной программе, вернувших результат <tex> true </tex>. Само искомое максимальное паросочетание содержится в массиве <tex> \mathtt{matching}</tex>. | ||
| + | После того, как все вершины <tex>v \in V</tex> будут просмотрены, текущее паросочетание будет максимальным. | ||
| + | Корректность алгоритма следует из [[Теорема о максимальном паросочетании и дополняющих цепях|теоремы о максимальном паросочетании и дополняющих цепях]] и теоремы, описанной выше.<br> | ||
| − | + | ==Реализация== | |
| − | + | * Граф <tex>G\langle V, E \rangle</tex> хранится в матрице смежности <tex>g[i][j]</tex> размера <tex>n </tex> на <tex>n</tex> | |
| + | *<tex>n = |V|</tex> | ||
| − | + | '''bool''' dfs(v: '''int'''): | |
| + | '''if''' (used[v]) | ||
| + | '''return''' ''false'' | ||
| + | used[v] = ''true'' | ||
| + | '''for''' to '''in''' g[v] | ||
| + | '''if''' (matching[to] == -1 '''or''' dfs(matching[to])): | ||
| + | matching[to] = v | ||
| + | '''return''' ''true'' | ||
| + | '''return''' ''false'' | ||
| − | |||
| − | + | function '''main'''(): | |
| − | + | fill(matching, -1) | |
| − | + | '''for''' i = 1..n | |
| − | + | fill(used, ''false'') | |
| − | + | dfs(i) | |
| − | + | '''for''' i = 1..n | |
| − | + | '''if''' (matching[i] != -1) | |
| − | + | print(i, " ", matching[i]) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Время работы== | ==Время работы== | ||
| − | Итак, алгоритм Куна можно представить как серию из | + | :Итак, алгоритм Куна можно представить как серию из <tex>n</tex> запусков обхода в глубину на всём графе. |
| + | :Следовательно, всего этот алгоритм исполняется за время <tex>O(nm)</tex>, где <tex>m</tex> {{---}} количество рёбер, что в худшем случае есть <tex>O(n^3)</tex> | ||
| + | :Если явно задано разбиение графа на две доли размером <tex>n_1</tex> и <tex>n_2</tex>, то можно запускать <tex>\mathtt{dfs}</tex> только из вершин первой доли, поэтому весь алгоритм исполняется за время <tex>O(n_1m)</tex>. В худшем случае это составляет <tex>O(n_1^2n_2).</tex> | ||
| + | |||
| + | ==Ссылки== | ||
| + | |||
| + | * [[Теорема_о_максимальном_паросочетании_и_дополняющих_цепях|Теорема о максимальном паросочетании и дополняющих цепях]] | ||
| + | * [[Алгоритм Форда-Фалкерсона для поиска максимального паросочетания|Алгоритм Форда-Фалкерсона для поиска максимального паросочетания]] | ||
| − | ==Источники== | + | ==Источники информации== |
| − | Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — | + | *[http://e-maxx.ru/algo/kuhn_matching MAXimal :: algo :: Алгоритм Куна нахождения наибольшего паросочетания]<br> |
| + | * Асанов М., Баранский В., Расин В. {{---}} Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр. | ||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о паросочетании]] | ||
Текущая версия на 19:41, 4 сентября 2022
Теорема
| Теорема: |
Если из вершины не существует дополняющей цепи относительно паросочетания и паросочетание получается из изменением вдоль дополняющей цепи, тогда из не существует дополняющей цепи в . |
| Доказательство: |
|
Алгоритм
Задан граф , про который известно, что он двудольный, но разбиение не задано явно. Требуется найти наибольшее паросочетание в нём
Алгоритм можно описать так: сначала возьмём пустое паросочетание, а потом — пока в графе удаётся найти увеличивающую цепь, — будем выполнять чередование паросочетания вдоль этой цепи, и повторять процесс поиска увеличивающей цепи. Как только такую цепь найти не удалось — процесс останавливаем, — текущее паросочетание и есть максимальное.
В массиве хранятся паросочетания (Если паросочетания с вершиной не существует, то ). А — обычный массив "посещённостей" вершин в обходе в глубину (он нужен, чтобы обход в глубину не заходил в одну вершину дважды). Функция возвращает , если ей удалось найти увеличивающую цепь из вершины , при этом считается, что эта функция уже произвела чередование паросочетания вдоль найденной цепи.
Внутри функции просматриваются все рёбра, исходящие из вершины , и затем проверяется: если это ребро ведёт в ненасыщенную вершину , либо если эта вершина насыщена, но удаётся найти увеличивающую цепь рекурсивным запуском из , то мы говорим, что мы нашли увеличивающую цепь, и перед возвратом из функции с результатом производим чередование в текущем ребре: перенаправляем ребро, смежное с , в вершину .
В основной программе сначала указывается, что текущее паросочетание — пустое (массив заполняется числами ). Затем перебирается вершина , и из неё запускается обход в глубину , предварительно обнулив массив .
Стоит заметить, что размер паросочетания легко получить как число вызовов в основной программе, вернувших результат . Само искомое максимальное паросочетание содержится в массиве .
После того, как все вершины будут просмотрены, текущее паросочетание будет максимальным.
Корректность алгоритма следует из теоремы о максимальном паросочетании и дополняющих цепях и теоремы, описанной выше.
Реализация
- Граф хранится в матрице смежности размера на
bool dfs(v: int):
if (used[v])
return false
used[v] = true
for to in g[v]
if (matching[to] == -1 or dfs(matching[to])):
matching[to] = v
return true
return false
function main():
fill(matching, -1)
for i = 1..n
fill(used, false)
dfs(i)
for i = 1..n
if (matching[i] != -1)
print(i, " ", matching[i])
Время работы
- Итак, алгоритм Куна можно представить как серию из запусков обхода в глубину на всём графе.
- Следовательно, всего этот алгоритм исполняется за время , где — количество рёбер, что в худшем случае есть
- Если явно задано разбиение графа на две доли размером и , то можно запускать только из вершин первой доли, поэтому весь алгоритм исполняется за время . В худшем случае это составляет
Ссылки
Источники информации
- MAXimal :: algo :: Алгоритм Куна нахождения наибольшего паросочетания
- Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.