Реализация булевой функции схемой из функциональных элементов — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Глубина схемы)
м (rollbackEdits.php mass rollback)
 
(не показано 5 промежуточных версий 3 участников)
Строка 7: Строка 7:
 
{{Определение  
 
{{Определение  
 
|definition=
 
|definition=
−
Если входные и выходные сигналы — являются нулями и единицами, элемент называется '''логическим''' (англ. ''logic gate'').
+
Если входные и выходные сигналы являются нулями и единицами, элемент называется '''логическим''' (англ. ''logic gate'').
 
При подаче на входы логического элемента любой комбинации двоичных сигналов, на выходах также возникает сигнал — значение [[Определение булевой функции|булевой функции]].
 
При подаче на входы логического элемента любой комбинации двоичных сигналов, на выходах также возникает сигнал — значение [[Определение булевой функции|булевой функции]].
 
}}
 
}}
Строка 13: Строка 13:
 
Отождествление переменных осуществляется при помощи ветвления проводников.[[File:Отождествление.png|thumb|200px|Отождествление переменных]]
 
Отождествление переменных осуществляется при помощи ветвления проводников.[[File:Отождествление.png|thumb|200px|Отождествление переменных]]
  
−
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
+
Чтобы осуществить подстановку одной функции в другую, нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
 
[[File:Подстановка.png|thumb|200px|Подстановка]]
 
[[File:Подстановка.png|thumb|200px|Подстановка]]
  
Строка 56: Строка 56:
 
{{Теорема
 
{{Теорема
 
|statement =
 
|statement =
−
Для любых базисов <tex>~B_1</tex>, <tex>~B_2</tex> и функции <tex>~f</tex> верно неравенство <tex>~size_{B_2}(f) \le C_{(B_1,\;B_2)}size_{B_1}(f)</tex>, где константа <tex>~C</tex> зависит только от базисов <tex>~B_1</tex> и <tex>~B_2</tex>.
+
Для любых базисов <tex>~B_1</tex>, <tex>~B_2</tex> и функции <tex>~f</tex> верно неравенство <tex>~size_{B_2}(f) \leqslant C_{(B_1,\;B_2)}size_{B_1}(f)</tex>, где константа <tex>~C</tex> зависит только от базисов <tex>~B_1</tex> и <tex>~B_2</tex>.
 
|proof =
 
|proof =
−
Пусть базис <tex>~B_2</tex> состоит из функций <tex>~g_1, g_2, \ldots, g_n</tex>. Каждый функциональный элемент базиса <tex>~B_2</tex> можно собрать с помощью не более чем <tex>~size_{B_1}(g_i)</tex> элементов из базиса <tex>~B_1</tex>. Собрать <tex>f</tex> в базисе <tex>B_1</tex> можно следующим образом: заменить каждый элемент схемы <tex>f</tex> в базисе <tex>B_2</tex> на схему соответствующей функции в базисе <tex>B_1</tex>. Такая сборка использует не более чем в <tex>~C = \overset{n}{\underset{i=1}{\max}} \ size_{B_1}(g_i)</tex> раз больше функциональных элементов, чем соответствующая схема в <tex>B_2</tex>. Параметр <tex>~C</tex> зависит только от выбранных базисов.
+
Пусть базис <tex>~B_2</tex> состоит из функций <tex>~g_1, g_2, \ldots, g_n</tex>. Каждый функциональный элемент базиса <tex>~B_2</tex> можно собрать с помощью не более чем <tex>~size_{B_1}(g_i)</tex> элементов из базиса <tex>~B_1</tex>. Собрать <tex>f</tex> в базисе <tex>B_1</tex> можно следующим образом: заменить каждый элемент схемы <tex>f</tex> в базисе <tex>B_2</tex> на схему соответствующей функции в базисе <tex>B_1</tex>. Такая сборка использует не более чем в <tex>~C = \underset{i=1 \ldots n}{\max} \ size_{B_1}(g_i)</tex> раз больше функциональных элементов, чем соответствующая схема в <tex>B_2</tex>. Параметр <tex>~C</tex> зависит только от выбранных базисов.
 
}}
 
}}
  
Строка 73: Строка 73:
 
|about=аналогична теореме про схемную сложность
 
|about=аналогична теореме про схемную сложность
 
|statement =
 
|statement =
−
Для любых базисов <tex>~B_1</tex>, <tex>~B_2</tex> и функции <tex>~f</tex> верно неравенство <tex>~depth_{B_2}(f) \leq C_{(B_1,\;B_2)}depth_{B_1}(f)</tex>, где константа <tex>~C</tex> зависит только от базисов <tex>~B_1</tex> и <tex>~B_2</tex>. Доказательство аналогично доказательству предыдущей теоремы.
+
Для любых базисов <tex>~B_1</tex>, <tex>~B_2</tex> и функции <tex>~f</tex> верно неравенство <tex>~depth_{B_2}(f) \leqslant C_{(B_1,\;B_2)}depth_{B_1}(f)</tex>, где константа <tex>~C</tex> зависит только от базисов <tex>~B_1</tex> и <tex>~B_2</tex>. Доказательство аналогично доказательству предыдущей теоремы.
 
}}
 
}}
  

Текущая версия на 19:14, 4 сентября 2022

Логические элементы

Определение:
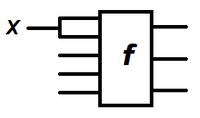
Функциональный элемент (англ. Combinational element) — устройство, предназначенное для обработки информации в цифровой форме. Функциональный элемент имеет входы и выходы. Сигналы на входах функционального элемента — аргументы функции, которую реализует функциональный элемент, сигналы на выходах — значение функции от аргументов.


Определение:
Если входные и выходные сигналы являются нулями и единицами, элемент называется логическим (англ. logic gate). При подаче на входы логического элемента любой комбинации двоичных сигналов, на выходах также возникает сигнал — значение булевой функции.


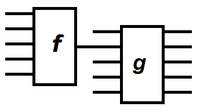
Отождествление переменных осуществляется при помощи ветвления проводников.
Отождествление переменных

Чтобы осуществить подстановку одной функции в другую, нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.

Подстановка

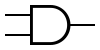
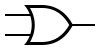
Изображение логических элементов на схемах

Тип элемента И ИЛИ НЕ Штрих Шеффера Стрелка Пирса
Традиционная форма AND logic element.png OR logic element.png NOT logic element.png NAND logic element.png NOR logic element.png
Прямоугольная форма AND logic relement.png

AND logic relement2.png

OR logic relement.png

OR logic relement2.png

NOT logic relement.png NAND logic relement.png

NAND logic relement2.png

NOR logic relement.png

NOR logic relement2.png

Схемная сложность

Определение:
Схемная сложность (англ. Circuit complexity) функции [math]f[/math] относительно базиса [math]B[/math] — это минимальное количество функциональных элементов из набора [math]B[/math], необходимое для реализации функции [math]f[/math] в базисе [math]B[/math]. Схемную сложность функции [math]f[/math] в базисе [math]B[/math] обозначают так: [math]size_B(f)[/math]


Теорема:
Для любых базисов [math]~B_1[/math], [math]~B_2[/math] и функции [math]~f[/math] верно неравенство [math]~size_{B_2}(f) \leqslant C_{(B_1,\;B_2)}size_{B_1}(f)[/math], где константа [math]~C[/math] зависит только от базисов [math]~B_1[/math] и [math]~B_2[/math].
Доказательство:
[math]\triangleright[/math]
Пусть базис [math]~B_2[/math] состоит из функций [math]~g_1, g_2, \ldots, g_n[/math]. Каждый функциональный элемент базиса [math]~B_2[/math] можно собрать с помощью не более чем [math]~size_{B_1}(g_i)[/math] элементов из базиса [math]~B_1[/math]. Собрать [math]f[/math] в базисе [math]B_1[/math] можно следующим образом: заменить каждый элемент схемы [math]f[/math] в базисе [math]B_2[/math] на схему соответствующей функции в базисе [math]B_1[/math]. Такая сборка использует не более чем в [math]~C = \underset{i=1 \ldots n}{\max} \ size_{B_1}(g_i)[/math] раз больше функциональных элементов, чем соответствующая схема в [math]B_2[/math]. Параметр [math]~C[/math] зависит только от выбранных базисов.
[math]\triangleleft[/math]

Глубина схемы

Определение:
Глубина схемы для функции [math]f[/math] относительно базиса [math]B[/math] (англ. Circuit depth) — это максимальная длина пути от входа до выхода по схеме соответствующей функции [math]f[/math], состоящей из элементов набора [math]B[/math], где за единицу длины принимается один элемент схемы. Глубину схемы для функции [math]f[/math] в базисе [math]B[/math] обозначают [math]depth_B(f)[/math]

Примечание: понятие глубины имеет смысл только для схем с ограниченной степенью входа (bounded fan-in).


Теорема (аналогична теореме про схемную сложность):
Для любых базисов [math]~B_1[/math], [math]~B_2[/math] и функции [math]~f[/math] верно неравенство [math]~depth_{B_2}(f) \leqslant C_{(B_1,\;B_2)}depth_{B_1}(f)[/math], где константа [math]~C[/math] зависит только от базисов [math]~B_1[/math] и [math]~B_2[/math]. Доказательство аналогично доказательству предыдущей теоремы.

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Реализация_булевой_функции_схемой_из_функциональных_элементов&oldid=84684»