Техника частичного каскадирования — различия между версиями
(Добавлены категории) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 47 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition='''Каталог''' (англ. ''catalog''){{---}} упорядоченный массив из элементов, на которых введено отношение порядка. В данной статье предполагается, что массив упорядочен по неубыванию. | + | |definition='''Каталог''' (англ. ''catalog'') {{---}} упорядоченный массив из элементов, на которых введено [[Отношение порядка|отношение порядка]]. В данной статье предполагается, что массив упорядочен по неубыванию. |
}} | }} | ||
{{Определение | {{Определение | ||
| Строка 12: | Строка 12: | ||
[[Файл:FCT_pic1.jpg|500px|right|thumb|Пример ответа на запрос]] | [[Файл:FCT_pic1.jpg|500px|right|thumb|Пример ответа на запрос]] | ||
Пусть <tex> n = \sum\limits_{i = 1}^k n_i </tex>. | Пусть <tex> n = \sum\limits_{i = 1}^k n_i </tex>. | ||
| + | # Для ответа на запрос последовательно посетим все каталоги. Пусть мы находимся в <tex> i</tex>-м каталоге, тогда мы можем ответить на запрос для данного каталога за <tex> O(\log n_i) </tex>, используя [[Целочисленный двоичный поиск|бинарный поиск]]. Так как каталогов <tex> k </tex> штук, то для ответа на запрос понадобится <tex> O(k \log n) </tex> времени. Для хранения всех каталогов понадобится <tex> O(n) </tex> памяти. | ||
| + | # Для второго способа построим сбалансированное бинарное дерево поиска из всех элементов всех каталогов. В каждой вершине дерева со значением будет храниться дополнительно кортеж из <tex> k </tex> элементов {{---}} максимальных представителей каждого каталога меньше либо равных данному значению. Таким образом такая структура будет занимать <tex> O(n) </tex> на дерево поиска и <tex> O(kn) </tex> на дополнительные кортежи. Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный <tex> x </tex> и выведем <tex> k </tex> элементов соответствующего кортежа, итого ответ на запрос производится за <tex> O(\log n + k) </tex>. | ||
| + | Пример работы второго алгоритма: пусть <tex> C_1 = \{1, 2, 3\}</tex>, <tex> C_2 = \{2, 3, 4\} </tex>, <tex> C_3 = \{1, 3, 4\} </tex> и запрос <tex> x = 2 </tex>. | ||
| + | *Построим кортежи для каждого значения по определению выше.<br><tex> key_1 = 1 \Leftrightarrow p_1 = \{1, \emptyset, 1\} </tex><br><tex> key_2 = 2 \Leftrightarrow p_2 = \{2, 2, 1\} </tex><br><tex> key_3 = 3 \Leftrightarrow p_3 = \{3, 3, 3\} </tex><br><tex> key_4 = 4 \Leftrightarrow p_4 = \{3, 4, 4\} </tex>. <br> <tex> key_i </tex> {{---}} значение, которое попадает в дерево поиска, <tex> p_i </tex> кортеж из элементов, который соответствует <tex> key_i </tex>. | ||
| + | *Для ответа на запрос найдем в дереве поиска ключ максимальный <tex> key \leqslant x </tex>, для <tex> x = 2 </tex> ключ <tex> key = key_2 = 2 </tex>, тогда в качестве ответа будет выступать кортеж <tex> p_2 </tex>. | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
Итого имеем: | Итого имеем: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Строка 22: | Строка 23: | ||
! Тип подхода к решению !! Необходимая память !! Время ответа на один запрос | ! Тип подхода к решению !! Необходимая память !! Время ответа на один запрос | ||
|- | |- | ||
| − | | <center><tex> k </tex> бинарных поисков </center> || <center><tex> | + | | <center><tex> k </tex> [[Целочисленный двоичный поиск|бинарных поисков]] </center> || <center><tex> O(n) </tex></center> || <center><tex> O(k \log n) </tex></center> |
|- | |- | ||
| <center>Построение бинарного дерева поиска с кортежами</center> || <center><tex> O(kn) </tex></center> || <center><tex> O(\log n + k) </tex></center> | | <center>Построение бинарного дерева поиска с кортежами</center> || <center><tex> O(kn) </tex></center> || <center><tex> O(\log n + k) </tex></center> | ||
| Строка 31: | Строка 32: | ||
<br> | <br> | ||
Идея данной техники построена на следующем: <br> | Идея данной техники построена на следующем: <br> | ||
| − | + | # Мы можем проводить ссылки из каталога номер <tex> i </tex> в <tex> (i + 1) </tex>-й каталог таким образом, что разница между элементами, соединенными ссылками минимальна, что, в некоторых случаях уменьшит время поиска элемента в следующем каталоге, так как область поиска сожмется. <br> | |
| − | + | # Мы можем для оптимизации пункта 1 создать модифицированные каталоги <tex> M_i </tex>, где <tex> i </tex>-й каталог будет представлять каталог <tex> C_i </tex> слитый с <tex> M_{i + 1} </tex> | |
=== Построение === | === Построение === | ||
| − | + | Будем называть подставным элементом такой элемент каталога <tex> M_i </tex>, который пришел из каталога <tex> M_{i + 1} </tex>. Сами каталоги <tex> M_i </tex> будем называть модифицированными каталогами. | |
| − | + | ||
| − | + | [[Файл:FCT_pic2.jpg|800px|left|thumb|Построение модифицированных каталогов]] | |
| − | + | '''Первый этап построения''': | |
| − | [[Файл:FCT_pic2.jpg| | ||
| − | |||
*<tex> i = k </tex> : Данный каталог не имеет никаких ссылок и равен <tex> C_i </tex>. | *<tex> i = k </tex> : Данный каталог не имеет никаких ссылок и равен <tex> C_i </tex>. | ||
*<tex> i < k </tex> : Для построения данного каталога будем сливать каталог <tex> C_i </tex> с каждым вторым элементом каталога <tex> M_{i + 1} </tex>. Каждый элемент из каталога <tex> M_{i + 1} </tex> оснастим ссылкой на позицию, откуда мы его взяли, такие ссылки будет называть ссылками вниз. | *<tex> i < k </tex> : Для построения данного каталога будем сливать каталог <tex> C_i </tex> с каждым вторым элементом каталога <tex> M_{i + 1} </tex>. Каждый элемент из каталога <tex> M_{i + 1} </tex> оснастим ссылкой на позицию, откуда мы его взяли, такие ссылки будет называть ссылками вниз. | ||
| − | + | '''Второй этап построения''': | |
| − | + | * В каждом модифицированном каталоге для каждого элемента заведем две ссылки. Для неподставных элементов это будут ссылки на максимальный подставной элемент меньше текущего и на минимальный любого типа больше текущего. Если элемент подставной, то ссылки будут на минимальный неподставной элемент больше текущего и на максимальный неподставной элемент меньше текущего. Назовем их ссылками влево и вправо. | |
<br> Рассмотрим на процесс построения на примере. | <br> Рассмотрим на процесс построения на примере. | ||
| Строка 54: | Строка 53: | ||
<br> <tex> C_4 = \{3, 4, 8, 10, 12\} </tex> | <br> <tex> C_4 = \{3, 4, 8, 10, 12\} </tex> | ||
<br> <tex> C_5 = \{1, 2, 4, 6, 9\} </tex> | <br> <tex> C_5 = \{1, 2, 4, 6, 9\} </tex> | ||
| − | <br> Для наглядности заведем таблицу, где в <tex>i</tex>- | + | <br> Для наглядности заведем таблицу, где в <tex>i</tex>-й строке <tex> j </tex>-я ячейка будет окрашена в зеленый цвет, если она присутствует в каталоге <tex> C_i </tex>. Тогда результатом построения будет таблица, которая представлена на рисунке. Для упрощения рисунка ссылки вправо из неподставных элементов не были отображены, их следует воспринимать как следующий справа от рассматриваемого элемент в ряду таблицы любого цвета. |
<br> | <br> | ||
Из-за необходимости хранения ссылок будет удобно завести структуру для хранения элементов в модифицированных каталогах: | Из-за необходимости хранения ссылок будет удобно завести структуру для хранения элементов в модифицированных каталогах: | ||
| − | struct | + | '''struct''' Node: |
| − | + | '''T''' key | |
| − | + | '''Node''' left, right, down | |
| − | bool is_alien | + | '''bool''' is_alien |
Псевдокод построения модифицированных каталогов: | Псевдокод построения модифицированных каталогов: | ||
M[k] = C[k] | M[k] = C[k] | ||
| − | '''for''' i = k - 1 ''' | + | '''for''' i = k - 1 '''downto''' 1 |
| − | pointer_in_C = 1 | + | '''int''' pointer_in_C = 1 <font color=green>// указатель на самый левый элемент каталога C[i], который еще не рассмотрели </font> |
| − | pointer_in_next_M = 1 | + | '''int''' pointer_in_next_M = 1 <font color=green>// указатель на самый левый элемент каталога M[i + 1], который еще не рассмотрели </font> |
| − | pointer_in_M = 1 | + | '''int''' pointer_in_M = 1 <font color=green>// указатель на самый левый элемент каталога M[i], в который будем добавлять элемент </font> |
| − | last_non_alien = | + | '''Node''' last_non_alien = <tex> \varnothing </tex> <font color=green>// указатель на последний неподставной элемент для текущей позиции </font> |
| − | last_alien = | + | '''Node''' last_alien = <tex> \varnothing </tex> <font color=green>// указатель на последний подставной элемент для текущей позиции</font> |
| − | '''while'' | + | '''while''' ''true'' |
| − | '''if''' | + | '''if''' pointer_in_next_M > M[i + 1].size '''and''' pointer_in_C > C[i].size |
'''break''' | '''break''' | ||
| − | '''if''' | + | '''if''' pointer_in_next_M > M[i + 1].size '''or''' M[i + 1][pointer_in_next_M] <tex> \geqslant </tex> C[i][pointer_in_C] |
M[i][pointer_in_M].key = C[i][pointer_in_C].key | M[i][pointer_in_M].key = C[i][pointer_in_C].key | ||
| − | M[i][pointer_in_M]. | + | M[i][pointer_in_M].left= last_alien |
last_non_alien = M[i][pointer_in_M] | last_non_alien = M[i][pointer_in_M] | ||
pointer_in_C++ | pointer_in_C++ | ||
| Строка 81: | Строка 80: | ||
M[i][pointer_in_M].key = M[i + 1][pointer_in_next_M].key | M[i][pointer_in_M].key = M[i + 1][pointer_in_next_M].key | ||
M[i][pointer_in_M].down = M[i + 1][pointer_in_next_M] | M[i][pointer_in_M].down = M[i + 1][pointer_in_next_M] | ||
| − | M[i][pointer_in_M].is_alien = | + | M[i][pointer_in_M].is_alien = ''true'' |
M[i][pointer_in_M].left = last_non_alien | M[i][pointer_in_M].left = last_non_alien | ||
| − | + | last_alien = M[i][pointer_in_M] | |
pointer_in_next_M += 2 | pointer_in_next_M += 2 | ||
pointer_in_M++ | pointer_in_M++ | ||
| − | + | '''if''' '''not''' M[i][M[i].size].is_alien | |
| − | '''for''' j = M[i].size - 1 ''' | + | last_non_alien = M[i][M[i].size] |
| − | if | + | '''else''' |
| + | last_non_alien = <tex> \varnothing </tex> <font color=green>// теперь last_non_alien указатель на первый справа неподставной элемент для текущей позиции</font> | ||
| + | '''for''' j = M[i].size - 1 '''downto''' 1 | ||
| + | '''if''' M[i][j].is_alien | ||
M[i][j].right = last_non_alien | M[i][j].right = last_non_alien | ||
| − | else | + | '''else''' |
M[i][j].right = M[i][j + 1] | M[i][j].right = M[i][j + 1] | ||
last_non_alien = M[i][j] | last_non_alien = M[i][j] | ||
| − | Из построения понятно, что мы тратим <tex> O(n_k) </tex> на построение последнего каталога, <tex> O(n_{k-1} + n_k / 2) </tex> на построение предпоследнего и т.д. Пусть <tex> p = 2^{ | + | Из построения понятно, что мы тратим <tex> O(n_k) </tex> на построение последнего каталога, <tex> O(n_{k-1} + n_k / 2) </tex> на построение предпоследнего и т.д. Пусть <tex> p = 2^{n - 1} </tex>. Тогда получаем оценку <tex> O(n_k (1 + 1/2 + 1/4 + \dots + 1/p) + n_{k - 1} (1 + 1/2 + 1/4 + \dots + 1/(p/2)) + \dots + n_1 ) </tex> <tex> = O(2 n_k + 2 n_{k -1} + \dots n_1) = O(n) </tex> памяти. По алгоритму понятно, что такая же оценка верна и для времени на предподсчет. |
| + | |||
=== Ответ на запрос === | === Ответ на запрос === | ||
| − | В первом каталоге ответ на запрос найдем с помощью бинарного поиска по <tex> | + | *В первом каталоге ответ на запрос найдем с помощью [[Целочисленный двоичный поиск|бинарного поиска]] по <tex> M_1 </tex>. Пусть ответом для этого каталога будет ячейка <tex> cell </tex>, тогда если <tex> cell </tex> {{---}} подставная вершина, то перейдем по ссылке влево. |
| + | *Проитерируемся по оставшимся каталогам. | ||
| + | **Для того, чтобы перейти в новый модифицированный каталог мы перейдем из <tex> cell </tex> по ссылке влево, чтобы попасть в подставную вершину, а потом из нее перейдем по ссылке вниз, чтобы попасть в следующий каталог. | ||
| + | **Если теперь <tex> cell </tex> {{---}} неподставная вершина, то нам достаточно рассмотреть двух ее соседей справа в <tex> C_i </tex>, так как <tex> cell.key \leqslant x </tex>, а каждая вторая ячейка из <tex> M_i </tex> попадает в <tex> M_{i - 1} </tex>, т.е. мы бы встретили ее ранее и перешли мы вниз по ней, но этого не случилось. | ||
| + | **Обновив <tex> cell </tex> максимальным из подходящих значений нужно проверить, является ли она подставным элементом, если да, то перейдем по ссылке влево, попав в ответ для текущего каталога, иначе это и будет ответ. | ||
| − | + | '''Node''' cell = binary_search(M[1], x) | |
| − | if | + | '''if''' cell.is_alien |
cell = cell.left | cell = cell.left | ||
| − | ans[1] = cell.key; | + | ans[1] = cell.key; <font color=green>// ans[i] - ответ на текущий запрос для каталога С[i] </font> |
'''for''' i = 2 '''to''' k | '''for''' i = 2 '''to''' k | ||
| − | cell = cell.left.down | + | cell = cell.left.down |
| − | if | + | '''if''' cell.right <tex> \leqslant </tex> x <font color=green>// Попытка сдвинуться к большему элементу </font> |
| − | cell = cell.right | + | cell = cell.right |
| − | if | + | '''if''' cell.right <tex> \leqslant </tex> x <font color=green>// Попытка сдвинуться к большему элементу </font> |
| − | cell = cell.right | + | cell = cell.right <font color=green>// Замечание: по построению, если мы стоим в ''неподставном элементе'', то при сдвиге вправо мы можем оказаться в элементе любого типа</font> |
| − | if | + | '''if''' cell.is_alien <font color=green>// Для этого есть проверка </font> |
cell = cell.left | cell = cell.left | ||
ans[i] = cell.key | ans[i] = cell.key | ||
| − | Как можно видеть, для того, чтобы найти ответ для первого каталога необходимо сделать один бинарный поиск, что требует <tex> O(\log n) </tex> времени, после чего необходимо <tex> O(k) </tex> времени, чтобы ответить на запрос для всех остальных каталогов. Суммарное время работы <tex> O(\log n + k) </tex>. | + | Как можно видеть, для того, чтобы найти ответ для первого каталога необходимо сделать один [[Целочисленный двоичный поиск|бинарный поиск]], что требует <tex> O(\log n) </tex> времени, после чего необходимо <tex> O(k) </tex> времени, чтобы ответить на запрос для всех остальных каталогов. Суммарное время работы <tex> O(\log n + k) </tex>. |
| + | <br> | ||
| + | |||
| + | ====Примеры ответа на запрос==== | ||
| + | {| border="0" cellpadding="5" cellspacing="0" center | ||
| + | |[[Файл:FCT_pic3.jpg|600px|center|thumb|Ответ на запрос <tex> x = 9 </tex>]] | ||
| + | |[[Файл:FCT_pic4.jpg|600px|center|thumb|Ответ на запрос <tex> x = 6 </tex>]] | ||
| + | |} | ||
| + | Рассмотрим, как будет происходить ответ на запрос для <tex> x = 9 </tex> (картинка справа) и для <tex> x = 6 </tex> (картинка слева). Каталоги взяты из примера для [[Техника частичного каскадирования#Построение | построения]]. Оставлены только ссылки, по которым осуществляется переход, а элементы пронумерованы в порядке обхода. | ||
| + | <br> | ||
| + | |||
| + | ===Дополнительно=== | ||
| + | Данная техника может использоваться для ускорения некоторых алгоритмов, где требуется ответить на запрос на отрезке <tex> [L, R] </tex>, где <tex> L, R \in R^n, n \in \mathbb N </tex>. Однако иногда наблюдается замедление<ref>[http://codeforces.com/blog/entry/21892?locale=en Fractional cascading is in fact slow? ifsmirnov's blog]</ref>. | ||
| + | |||
| + | ==См. также== | ||
| + | *[[Пересечение прямоугольника с множеством непересекающихся отрезков (segment tree)]] | ||
| + | *[[Перечисление точек в произвольном прямоугольнике за n * log ^(d - 1) n (range tree)]] | ||
| + | == Примечания == | ||
| + | <references /> | ||
== Ссылки == | == Ссылки == | ||
* [http://www.hpl.hp.com/techreports/Compaq-DEC/SRC-RR-12.pdf Fractional Cascading. Bernard Chazelle and Leonidas J. Guibas] | * [http://www.hpl.hp.com/techreports/Compaq-DEC/SRC-RR-12.pdf Fractional Cascading. Bernard Chazelle and Leonidas J. Guibas] | ||
Текущая версия на 19:15, 4 сентября 2022
| Определение: |
| Каталог (англ. catalog) — упорядоченный массив из элементов, на которых введено отношение порядка. В данной статье предполагается, что массив упорядочен по неубыванию. |
| Определение: |
| Техника частичного каскадирования (англ. fractional cascading technique) — это способ организации структуры данных, который предназначен для быстрого итеративного поиска в каталогах. |
| Задача: |
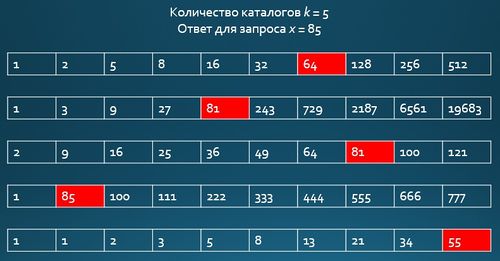
| Дано каталогов , каталог имеет размер . Поступают запросы, которые представляют собой один элемент . Требуется для каждого запроса определить в каждом каталоге максимальный элемент меньше либо равный . |
Различные подходы к решению
Пусть .
- Для ответа на запрос последовательно посетим все каталоги. Пусть мы находимся в -м каталоге, тогда мы можем ответить на запрос для данного каталога за , используя бинарный поиск. Так как каталогов штук, то для ответа на запрос понадобится времени. Для хранения всех каталогов понадобится памяти.
- Для второго способа построим сбалансированное бинарное дерево поиска из всех элементов всех каталогов. В каждой вершине дерева со значением будет храниться дополнительно кортеж из элементов — максимальных представителей каждого каталога меньше либо равных данному значению. Таким образом такая структура будет занимать на дерево поиска и на дополнительные кортежи. Тогда для ответа на запрос найдем в дереве поиска максимальный ключ меньше либо равный и выведем элементов соответствующего кортежа, итого ответ на запрос производится за .
Пример работы второго алгоритма: пусть , , и запрос .
- Построим кортежи для каждого значения по определению выше.
.
— значение, которое попадает в дерево поиска, кортеж из элементов, который соответствует . - Для ответа на запрос найдем в дереве поиска ключ максимальный , для ключ , тогда в качестве ответа будет выступать кортеж .
Итого имеем:
| Тип подхода к решению | Необходимая память | Время ответа на один запрос |
|---|---|---|
| |
|
|
| |
|
|
Решение с помощью техники частичного каскадирования
Как будет показано далее, эта техника берет лучшее от подходов к решению этой задачи, что были рассмотрены выше, а именно она требует памяти и времени для ответа на запрос.
Идея данной техники построена на следующем:
- Мы можем проводить ссылки из каталога номер в -й каталог таким образом, что разница между элементами, соединенными ссылками минимальна, что, в некоторых случаях уменьшит время поиска элемента в следующем каталоге, так как область поиска сожмется.
- Мы можем для оптимизации пункта 1 создать модифицированные каталоги , где -й каталог будет представлять каталог слитый с
Построение
Будем называть подставным элементом такой элемент каталога , который пришел из каталога . Сами каталоги будем называть модифицированными каталогами.
Первый этап построения:
- : Данный каталог не имеет никаких ссылок и равен .
- : Для построения данного каталога будем сливать каталог с каждым вторым элементом каталога . Каждый элемент из каталога оснастим ссылкой на позицию, откуда мы его взяли, такие ссылки будет называть ссылками вниз.
Второй этап построения:
- В каждом модифицированном каталоге для каждого элемента заведем две ссылки. Для неподставных элементов это будут ссылки на максимальный подставной элемент меньше текущего и на минимальный любого типа больше текущего. Если элемент подставной, то ссылки будут на минимальный неподставной элемент больше текущего и на максимальный неподставной элемент меньше текущего. Назовем их ссылками влево и вправо.
Рассмотрим на процесс построения на примере.
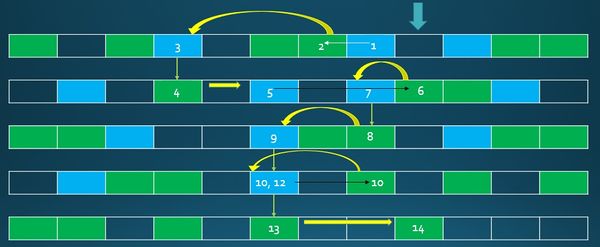
Пусть дано каталогов:
Для наглядности заведем таблицу, где в -й строке -я ячейка будет окрашена в зеленый цвет, если она присутствует в каталоге . Тогда результатом построения будет таблица, которая представлена на рисунке. Для упрощения рисунка ссылки вправо из неподставных элементов не были отображены, их следует воспринимать как следующий справа от рассматриваемого элемент в ряду таблицы любого цвета.
Из-за необходимости хранения ссылок будет удобно завести структуру для хранения элементов в модифицированных каталогах:
struct Node:
T key
Node left, right, down
bool is_alien
Псевдокод построения модифицированных каталогов:
M[k] = C[k]
for i = k - 1 downto 1
int pointer_in_C = 1 // указатель на самый левый элемент каталога C[i], который еще не рассмотрели
int pointer_in_next_M = 1 // указатель на самый левый элемент каталога M[i + 1], который еще не рассмотрели
int pointer_in_M = 1 // указатель на самый левый элемент каталога M[i], в который будем добавлять элемент
Node last_non_alien = // указатель на последний неподставной элемент для текущей позиции
Node last_alien = // указатель на последний подставной элемент для текущей позиции
while true
if pointer_in_next_M > M[i + 1].size and pointer_in_C > C[i].size
break
if pointer_in_next_M > M[i + 1].size or M[i + 1][pointer_in_next_M] C[i][pointer_in_C]
M[i][pointer_in_M].key = C[i][pointer_in_C].key
M[i][pointer_in_M].left= last_alien
last_non_alien = M[i][pointer_in_M]
pointer_in_C++
else
M[i][pointer_in_M].key = M[i + 1][pointer_in_next_M].key
M[i][pointer_in_M].down = M[i + 1][pointer_in_next_M]
M[i][pointer_in_M].is_alien = true
M[i][pointer_in_M].left = last_non_alien
last_alien = M[i][pointer_in_M]
pointer_in_next_M += 2
pointer_in_M++
if not M[i][M[i].size].is_alien
last_non_alien = M[i][M[i].size]
else
last_non_alien = // теперь last_non_alien указатель на первый справа неподставной элемент для текущей позиции
for j = M[i].size - 1 downto 1
if M[i][j].is_alien
M[i][j].right = last_non_alien
else
M[i][j].right = M[i][j + 1]
last_non_alien = M[i][j]
Из построения понятно, что мы тратим на построение последнего каталога, на построение предпоследнего и т.д. Пусть . Тогда получаем оценку памяти. По алгоритму понятно, что такая же оценка верна и для времени на предподсчет.
Ответ на запрос
- В первом каталоге ответ на запрос найдем с помощью бинарного поиска по . Пусть ответом для этого каталога будет ячейка , тогда если — подставная вершина, то перейдем по ссылке влево.
- Проитерируемся по оставшимся каталогам.
- Для того, чтобы перейти в новый модифицированный каталог мы перейдем из по ссылке влево, чтобы попасть в подставную вершину, а потом из нее перейдем по ссылке вниз, чтобы попасть в следующий каталог.
- Если теперь — неподставная вершина, то нам достаточно рассмотреть двух ее соседей справа в , так как , а каждая вторая ячейка из попадает в , т.е. мы бы встретили ее ранее и перешли мы вниз по ней, но этого не случилось.
- Обновив максимальным из подходящих значений нужно проверить, является ли она подставным элементом, если да, то перейдем по ссылке влево, попав в ответ для текущего каталога, иначе это и будет ответ.
Node cell = binary_search(M[1], x)
if cell.is_alien
cell = cell.left
ans[1] = cell.key; // ans[i] - ответ на текущий запрос для каталога С[i]
for i = 2 to k
cell = cell.left.down
if cell.right x // Попытка сдвинуться к большему элементу
cell = cell.right
if cell.right x // Попытка сдвинуться к большему элементу
cell = cell.right // Замечание: по построению, если мы стоим в неподставном элементе, то при сдвиге вправо мы можем оказаться в элементе любого типа
if cell.is_alien // Для этого есть проверка
cell = cell.left
ans[i] = cell.key
Как можно видеть, для того, чтобы найти ответ для первого каталога необходимо сделать один бинарный поиск, что требует времени, после чего необходимо времени, чтобы ответить на запрос для всех остальных каталогов. Суммарное время работы .
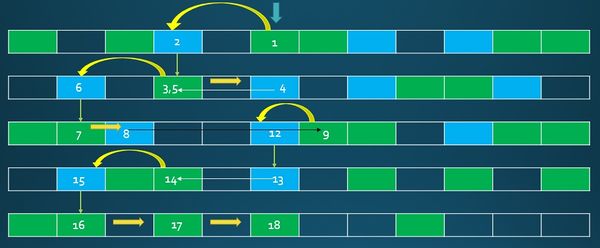
Примеры ответа на запрос
Рассмотрим, как будет происходить ответ на запрос для (картинка справа) и для (картинка слева). Каталоги взяты из примера для построения. Оставлены только ссылки, по которым осуществляется переход, а элементы пронумерованы в порядке обхода.
Дополнительно
Данная техника может использоваться для ускорения некоторых алгоритмов, где требуется ответить на запрос на отрезке , где . Однако иногда наблюдается замедление[1].