Панциклический граф — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 12 промежуточных версий 6 участников) | |||
| Строка 6: | Строка 6: | ||
{{Определение | {{Определение | ||
|definition='''<tex> r </tex>-панциклический граф''' (англ. ''<tex> r </tex>-pancyclic graph'') {{---}} граф содержит все циклы от <tex> r </tex> до <tex> n </tex>. | |definition='''<tex> r </tex>-панциклический граф''' (англ. ''<tex> r </tex>-pancyclic graph'') {{---}} граф содержит все циклы от <tex> r </tex> до <tex> n </tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Строка 25: | Строка 18: | ||
|proof= | |proof= | ||
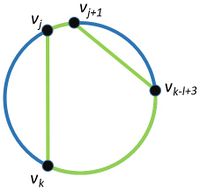
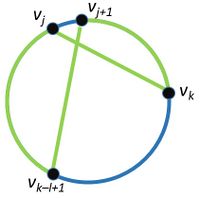
| − | [[Файл:Circle 1.jpg|200px|left|thumb| | + | [[Файл:Circle 1.jpg|200px|left|thumb| <tex> v_k </tex> на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j -1}) </tex> и ребра (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+3}</tex>) выделены. Дуги и ребра, окрашенные в зеленый цвет, образуют цикл длины l]] [[Файл:Circle 2.jpg|200px|right|thumb| <tex> v_k </tex> на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex> и ребра (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+1}</tex>) выделены. Дуги и ребра, окрашенные в зеленый цвет, образуют цикл длины l]] |
Обозначим как <tex> C=v_1 v_2 v_3 \ldots v_n </tex> гамильтонов цикл в графе <tex> G </tex>. Для простоты расположим <tex> C </tex> на окружности. Также подразумевается, что все индексы при вершинах берутся по модулю, то есть <tex> v_j = v_{((j - 1)\bmod n) + 1} </tex>. | Обозначим как <tex> C=v_1 v_2 v_3 \ldots v_n </tex> гамильтонов цикл в графе <tex> G </tex>. Для простоты расположим <tex> C </tex> на окружности. Также подразумевается, что все индексы при вершинах берутся по модулю, то есть <tex> v_j = v_{((j - 1)\bmod n) + 1} </tex>. | ||
| − | Пусть в | + | Пусть граф не панциклический, тогда в неи нет цикла длины <tex> l </tex>, <tex> 3 \leqslant l \leqslant n-1 </tex> (по условию в графе существует гамильтонов цикл, длина которого равна <tex> n </tex>). Рассмотрим две соседние вершины <tex> v_j v_{j+1} </tex> и вместе с ними рассмотрим следующие пары: |
| − | Для <tex>k</tex> таких, что <tex> v_k </tex> лежит на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j -1}) </tex> рассмотрим пары (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+3}</tex> | + | Для <tex>k</tex> таких, что <tex> v_k </tex> лежит на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j -1}) </tex> рассмотрим пары (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+3}</tex>) |
| − | Для <tex>k</tex> таких, что <tex> v_k </tex> лежит на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex> рассмотрим пары (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+1}</tex> | + | Для <tex>k</tex> таких, что <tex> v_k </tex> лежит на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex> рассмотрим пары (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+1}</tex>) |
| − | При добавлении таких пар ребер в графе появляется цикл длины <tex> l </tex> | + | При добавлении таких пар ребер в графе появляется цикл длины <tex> l </tex>. Действительно: |
| + | *Рассмотрим первый случай, когда <tex> v_k </tex> лежит на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j -1}) </tex> и существуют ребра (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+3}</tex>). Длина цикла равна <tex> len((v_{k - l + 3}, v_{k - l + 4}, v_{k})) + 3 = k - (k - l + 3) + 3 = l - 3 + 3 = l </tex>. | ||
| + | *Рассмотрим второй случай, когда <tex> v_k </tex> лежит на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex> и существуют ребра (<tex>v_j, v_k</tex>) и (<tex>v_{j+1}, v_{k-l+1}</tex>). Тогда длина цикла равна <tex> len((v_{k}, v_{k - 1}, v_{k - l + 1})) - 1 + 2 = k - (k - l + 1) - 1 + 2 = l - 1 - 1 + 2 = l </tex>. | ||
| + | Значит в <tex> G </tex> может входить максимум одно ребро из таких пар. Тогда можно утверждать, что <tex> deg(v_j) + deg(v_{j + 1}) \leqslant n </tex>. | ||
| + | |||
| + | {{Лемма | ||
| + | |statement= | ||
| + | Если для графа <tex> G </tex> выполнены условия из теоремы и в нем отсутствует цикл длины <tex> l </tex>, <tex> 3 \leqslant l \leqslant n-1 </tex>, то количество вершин в графе четное | ||
| + | |proof= Доказательство будем вести методом от противного. | ||
| + | *Пусть <tex> n </tex> является нечетным, тогда из рассуждений выше существует вершина <tex> v_x </tex>, для которое верно, что <tex> deg(v_x) \leqslant \genfrac{}{}{}{0}{n-1}{2} </tex>. | ||
| + | **Пусть это не так, тогда <tex> \forall i, 1 \leqslant i \leqslant n : deg(v_i) \geqslant \genfrac{}{}{}{0}{n-1}{2} + 1 = \genfrac{}{}{}{0}{n+1}{2} </tex>, значит <tex> \forall j, 1 \leqslant j \leqslant n : deg(v_j) + deg(v_{j+1}) \geqslant \genfrac{}{}{}{0}{n+1}{2} + \genfrac{}{}{}{0}{n+1}{2} = n + 1 </tex>, то есть мы получили противоречие с тем, что <tex> deg(v_j) + deg(v_{j + 1}) \leqslant n </tex>. | ||
| + | *Без потери общности пусть <tex> v_x = v_n </tex>. Рассмотрим <tex> 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{\genfrac{}{}{}{}{n - 1}{2}} (deg(v_{2i-1}) + deg(v_{2i})) + deg(v_n) \leqslant \genfrac{}{}{}{0}{n(n-1)}{2} + </tex> <tex> \genfrac{}{}{}{0}{n-1}{2} < \genfrac{}{}{}{0}{n^2}{2} </tex>, то есть <tex> |E| < \genfrac{}{}{}{0}{n^2}{4} </tex>, но по условию <tex> |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex> {{---}} получили противоречие. | ||
| + | }} | ||
| − | + | По лемме <tex> n </tex> является четным, если в цикле отсутствует цикл длины <tex> l </tex>. Тогда верно, что <tex> 2|E| = \sum\limits_{i=1}^n deg(v_i) = \sum\limits_{i=1}^{\genfrac{}{}{}{}{n}{2}} (deg(v_{2i-1}) + deg(v_{2i})) \leqslant \genfrac{}{}{}{0}{n^2}{2} </tex>, а так как по условию <tex> |E| \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex>, то <tex> |E| = \genfrac{}{}{}{0}{n^2}{4} </tex>. Данное равенство достигается, если верно, что: | |
| − | |||
| − | |||
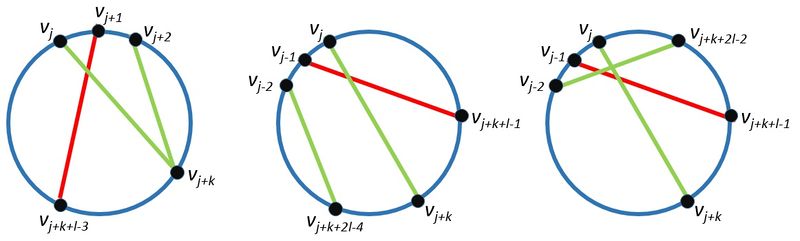
| − | [[Файл:Circle 3.jpg|800px|right]] | + | [[Файл:Circle 3.jpg|800px|right|thumb|Слева направо изображены случаи 1-3. Красным выделены ребра, которые не могут быть в рассматриваемом графе, если в нем присутствуют ребра, выделенные зеленым]] |
| − | *<tex> v_k </tex> лежит на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j - 1}) </tex>: <tex> (v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+3}) \notin E </tex> | + | *<tex> v_k </tex> лежит на дуге <tex> (v_{j + l - 1}, v_{j + l}, v_{j - 1}) </tex>: <tex> (v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+3}) \notin E </tex> или <tex> (v_j, v_k) \notin E </tex> и <tex>(v_{j+1}, v_{k-l+3}) \in E </tex> |
| − | *<tex> v_k </tex> лежит на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex>: <tex>(v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+1}) \notin E </tex> | + | *<tex> v_k </tex> лежит на дуге <tex> (v_{j + 2}, v_{j + 3}, v_{j + l - 2}) </tex>: <tex>(v_j, v_k) \in E </tex> и <tex>(v_{j+1}, v_{k-l+1}) \notin E </tex> или <tex>(v_j, v_k) \notin E </tex> и <tex>(v_{j+1}, v_{k-l+1}) \in E </tex> |
Пусть <tex> G </tex> не <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex>, тогда существует такое четное число <tex> k </tex>, что в графе <tex> G </tex> существует ребро <tex> (v_j, v_{j+k}) </tex>, то есть существует цикл нечетной длины. Докажем, что в таком случае существует ребро <tex> (v_j, v_{j+2}) \in E </tex>. Пусть это не так и минимальное четное <tex> k </tex>, что <tex> \exists (v_j, v_{j+k}) \in E </tex> больше двух, то есть <tex> k \geqslant 4 </tex>. Тогда существует три случая: | Пусть <tex> G </tex> не <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex>, тогда существует такое четное число <tex> k </tex>, что в графе <tex> G </tex> существует ребро <tex> (v_j, v_{j+k}) </tex>, то есть существует цикл нечетной длины. Докажем, что в таком случае существует ребро <tex> (v_j, v_{j+2}) \in E </tex>. Пусть это не так и минимальное четное <tex> k </tex>, что <tex> \exists (v_j, v_{j+k}) \in E </tex> больше двух, то есть <tex> k \geqslant 4 </tex>. Тогда существует три случая: | ||
| Строка 51: | Строка 54: | ||
# <tex> 4 \leqslant k \leqslant n - l </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j+1}, v_{j+k+l-3}) \notin E \Rightarrow (v_{j+2}, v_{j+k}) \in E </tex> <br> <tex> \exists l = k-2 : (v_i, v_{i+l}) \in E </tex> {{---}} противоречие с минимальностью <tex> k </tex> | # <tex> 4 \leqslant k \leqslant n - l </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j+1}, v_{j+k+l-3}) \notin E \Rightarrow (v_{j+2}, v_{j+k}) \in E </tex> <br> <tex> \exists l = k-2 : (v_i, v_{i+l}) \in E </tex> {{---}} противоречие с минимальностью <tex> k </tex> | ||
# <tex> n - l + 2 \leqslant k \leqslant 2n - 2l </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-4}) \in E </tex> <br> однако <tex> 2n - k - 2l + 2 \leqslant k - 2 </tex> {{---}} противоречие с минимальностью <tex> k </tex> | # <tex> n - l + 2 \leqslant k \leqslant 2n - 2l </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-4}) \in E </tex> <br> однако <tex> 2n - k - 2l + 2 \leqslant k - 2 </tex> {{---}} противоречие с минимальностью <tex> k </tex> | ||
| − | # <tex> 2n - 2l + 2 \leqslant k \leqslant n - 2 </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-2}) \in E </tex> <br> однако <tex> k + 2l - 2n \leqslant k - 2 </tex> {{---}} снова | + | # <tex> 2n - 2l + 2 \leqslant k \leqslant n - 2 </tex> <br> <tex> (v_j, v_{j+k}) \in E \Rightarrow (v_{j-1}, v_{j+k+l-1}) \notin E \Rightarrow (v_{j-2}, v_{j+k+2l-2}) \in E </tex> <br> однако <tex> k + 2l - 2n \leqslant k - 2 </tex> {{---}} снова противоречие с минимальностью выбранного k |
Таким образом, в <tex> G </tex> существует ребро <tex> (v_j, v_{j+2}) </tex>, но тогда <tex> (v_j, v_{j+l}) \notin E </tex>, а следовательно <tex> (v_{j+1}, v_{j+3}) \in E </tex>. Если продолжить по всему графу, то получим, что <tex> \forall j : (v_j, v_{j+2}) \in E </tex> и, как следствие, <tex> G </tex> {{---}} панциклический. | Таким образом, в <tex> G </tex> существует ребро <tex> (v_j, v_{j+2}) </tex>, но тогда <tex> (v_j, v_{j+l}) \notin E </tex>, а следовательно <tex> (v_{j+1}, v_{j+3}) \in E </tex>. Если продолжить по всему графу, то получим, что <tex> \forall j : (v_j, v_{j+2}) \in E </tex> и, как следствие, <tex> G </tex> {{---}} панциклический. | ||
| Строка 65: | Строка 68: | ||
#<tex> G </tex> = <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex> | #<tex> G </tex> = <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex> | ||
|proof=По [[Теорема Оре|теореме Оре]] <tex> G </tex> {{---}} гамильтонов граф. Покажем, что <tex> m \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex>. Пусть <tex> k </tex> {{---}} минимальная степень вершины в графе. | |proof=По [[Теорема Оре|теореме Оре]] <tex> G </tex> {{---}} гамильтонов граф. Покажем, что <tex> m \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex>. Пусть <tex> k </tex> {{---}} минимальная степень вершины в графе. | ||
| − | # <tex> k \geqslant \genfrac{}{}{}{ | + | # <tex> k \geqslant \genfrac{}{}{}{}{n}{2} </tex>, тогда <tex> 2m = \sum\limits_{i=1}^n deg(v_i) >= \sum\limits_{i=1}^n k = k n \geqslant \genfrac{}{}{}{0}{n^2}{2} </tex> |
| − | # <tex> k < \genfrac{}{}{}{ | + | # <tex> k < \genfrac{}{}{}{}{n}{2} </tex>. Пусть существует <tex> x </tex> вершин, так что их степени равны <tex> k </tex>, тогда они все должны быть связаны, так как иначе мы получим противоречие с утверждением теоремы <tex> \forall (u, v) \notin E : deg(u) + deg(v) \geqslant n </tex>. Понятно, что <tex> x \leqslant k + 1 </tex>, но так как граф является гамильтоновым, то он связен, а значит <tex> x < k + 1 </tex>. Несложно заметить, что если из всех <tex> x </tex> вершин степени <tex> k </tex> провести оставшиеся ребра в одну вершину, у которой степень больше, то в графе остенется как минимум <tex> n - k - 1 </tex> вершин, степени которых как минимум <tex> n - k </tex>, поскольку должно выполняться неравенство из теоермы. Тогда можно оценить количество ребер. <br> <tex> m \geqslant \genfrac{}{}{}{0}{1}{2}((n-k-1)(n-k)+k^2+(k+1)) = \genfrac{}{}{}{0}{1}{2}(n^2 - n(2k + 1) + 2k^2 + 2k + 1) \geqslant \genfrac{}{}{}{0}{n^2+1}{4} </tex> |
Таким образом <tex> m \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex> и согласно теореме граф либо панциклический, либо <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex>. | Таким образом <tex> m \geqslant \genfrac{}{}{}{0}{n^2}{4} </tex> и согласно теореме граф либо панциклический, либо <tex>K_{\genfrac{}{}{}{}{n}{2}, \genfrac{}{}{}{}{n}{2}}</tex>. | ||
Текущая версия на 19:34, 4 сентября 2022
Содержание
Основные определения
| Определение: |
| Панциклический граф (англ. pancyclic graph) — граф, в котором есть циклы всех длин от до . |
| Определение: |
| -панциклический граф (англ. -pancyclic graph) — граф содержит все циклы от до . |
Основная теорема
| Теорема (J. A. Bondy): | ||||||
Пусть — гамильтонов граф, .
Тогда верно одно из двух утверждений:
| ||||||
| Доказательство: | ||||||
|
Обозначим как гамильтонов цикл в графе . Для простоты расположим на окружности. Также подразумевается, что все индексы при вершинах берутся по модулю, то есть . Пусть граф не панциклический, тогда в неи нет цикла длины , (по условию в графе существует гамильтонов цикл, длина которого равна ). Рассмотрим две соседние вершины и вместе с ними рассмотрим следующие пары: Для таких, что лежит на дуге рассмотрим пары () и () Для таких, что лежит на дуге рассмотрим пары () и () При добавлении таких пар ребер в графе появляется цикл длины . Действительно:
Значит в может входить максимум одно ребро из таких пар. Тогда можно утверждать, что .
По лемме является четным, если в цикле отсутствует цикл длины . Тогда верно, что , а так как по условию , то . Данное равенство достигается, если верно, что:
Пусть не , тогда существует такое четное число , что в графе существует ребро , то есть существует цикл нечетной длины. Докажем, что в таком случае существует ребро . Пусть это не так и минимальное четное , что больше двух, то есть . Тогда существует три случая:
| ||||||
Следствие
| Утверждение: |
Пусть
Тогда верно одно из двух утверждений:
|
|
По теореме Оре — гамильтонов граф. Покажем, что . Пусть — минимальная степень вершины в графе.
|