Участник:Artem.ustinov/НВП — различия между версиями
м (→Обработка блока) |
(→Деление на блоки) |
||
| (не показано 10 промежуточных версий 2 участников) | |||
| Строка 170: | Строка 170: | ||
[[Цифровая сортировка]] каждого блока отдельно будет давать нам время работы <tex>O \left(\dfrac{n}{m}n \right) = O \left(\dfrac{n^2}{m} \right)</tex>. Дополним каждый элемент <tex>\pi</tex> номером блока, в котором он находится и смещением в этом блоке. Теперь, рассматривая номер блока как старший разряд, элемент как младший разряд (по смещению внутри блока не сортируем), можно сортировать цифровой сортировкой за линейное время <tex>O(n)</tex>, потому что значения элементов и номера блоков не превосходят <tex>n</tex>. | [[Цифровая сортировка]] каждого блока отдельно будет давать нам время работы <tex>O \left(\dfrac{n}{m}n \right) = O \left(\dfrac{n^2}{m} \right)</tex>. Дополним каждый элемент <tex>\pi</tex> номером блока, в котором он находится и смещением в этом блоке. Теперь, рассматривая номер блока как старший разряд, элемент как младший разряд (по смещению внутри блока не сортируем), можно сортировать цифровой сортировкой за линейное время <tex>O(n)</tex>, потому что значения элементов и номера блоков не превосходят <tex>n</tex>. | ||
| − | Перестановка смещений, образованная в сортированном блоке есть не что иное, как обратная перестановка перестановки, элементы которой соотносятся между собой как элементы исходного блока. | + | Перестановка смещений, образованная в сортированном блоке есть не что иное, как обратная перестановка перестановки <tex>\xi</tex>, элементы которой соотносятся между собой как элементы исходного блока. Т.е. если элемент <tex>\pi</tex> находится в исходной перестановке в блоке <tex>C_j</tex> на позиции <tex>i</tex>, то в блоке <tex>C_j^s</tex> он на позиции <tex>\xi_i</tex>. |
| − | == | + | ====Пример==== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | ||
Предположим, что <tex>m=5</tex>. Исходно получаем: | Предположим, что <tex>m=5</tex>. Исходно получаем: | ||
| Строка 221: | Строка 201: | ||
|} | |} | ||
| + | === Обработка блока === | ||
| + | Обрабатывая блок, каждому элементу <tex>x</tex> внутри этого блока взаимно однозначно сопоставим ключ <tex>y = \mathtt{key}(x);~x=\mathtt{elt}(y)</tex> так, чтобы их значения находились в промежутке <tex>\{1,2,\dots,2m\}</tex>. Очередь <tex>B</tex> будет работать непосредственно с ключами элементов. | ||
| + | |||
| + | Работая с блоком <tex>C_j</tex>, будем сливать элементы, ключи которых находятся в очереди <tex>B</tex>, с <tex>C_j^s</tex> в список <tex>\mathtt{merged}</tex>. Поскольку мы предположили, что <tex>m\geqslant k</tex>, то количество ключей в <tex>B</tex> не больше <tex>m</tex>, тогда длина <tex>\mathtt{merged}</tex> не больше <tex>2m</tex>, что позволяет однозначно определить ключи на множестве <tex>\{1,2,\dots,2m\}</tex>. Как было замечено ранее, элементы, чьи ключи находятся в <tex>B</tex>, располагаются в возрастающем порядке, поэтому возможно производить тривиальную операцию [[Сортировка слиянием#Принцип работы#Слияние двух массивов | слияния]] за <tex>O(m)</tex>. | ||
| + | |||
| + | В итоге, получим отсортированный список <tex>\mathtt{merged}</tex>. Сопоставим ключ каждому элементу как его позицию в этом списке, тогда справедливы утверждения, что <tex>\mathtt{elt}(x)=\mathtt{merged}[x]</tex> и <tex>(\pi_{i}<\pi_{k} \Longleftrightarrow \mathtt{key}(\pi_{i})<\mathtt{key}(\pi_{k}))</tex>, где <tex>\pi_{i},\pi_{k}\in \mathtt{merged}</tex>, поэтому любая возрастающая последовательность ключей элементов будет соответствовать возрастающей последовательности элементов. Таким образом, приоритетная очередь сможет корректно работать с ключами элементов. | ||
| + | |||
| + | Находим последовательность ключей, соответствующую элементам блока <tex>C_j^s</tex>. Действуя на эту последовательность перестановкой <tex>\xi_j</tex>, получаем последовательность ключей в порядке исходного блока. | ||
| + | |||
| + | Оставшиеся ключи, которые входят в <tex>\mathtt{merged}</tex>, но не являются ключами элементов в обрабатываемом блоке, будут ключами элементов из очереди <tex>B</tex>. Обновляем очередь <tex>B</tex> этими ключами. | ||
| + | |||
| + | Затем запускаем алгоритм <tex>\mathrm{LIS}</tex>, для ключей элементов <tex>C_j</tex> в порядке исходной последовательности. | ||
| + | |||
| + | В итоге, обработка блока делится на следующие этапы: | ||
| + | * Достаем из очереди <tex>B</tex> ключи <tex>x</tex>, конвертируем их в элементы <tex>\mathtt{elt}(x)</tex> и кладём в список <tex>\mathtt{elems}</tex>. | ||
| + | * Сливаем элементы в <tex>\mathtt{elems}</tex> со следующим отсортированным блоком <tex>C_j^s</tex> в список <tex>\mathtt{merged}</tex>, генерируя два вспомогательных массива <tex>\mathtt{ind_0}</tex> и <tex>\mathtt{ind_1}</tex>, хранящих индексы элементов списков <tex>C_j^s</tex> и <tex>\mathtt{elems}</tex> соответственно в списке <tex>\mathtt{merged}</tex>. | ||
| + | * Действуя на последовательность ключей в списке <tex>\mathtt{ind_0}</tex> перестановкой <tex>\xi_j</tex> получим ключи в порядке исходной последовательности. | ||
| + | * Вставляем в <tex>B</tex> новые ключи элементов списка <tex>\mathtt{elems}</tex> (элементы <tex>\mathtt{ind_1}</tex>). | ||
| + | * Обрабатываем ключи элементов блока в порядке исходной последовательности с помощью алгоритма <tex>\mathrm{LIS}</tex>. Для восстановления НВП также используем массив "предшественников", который будет работать с соответствующими ключам элементами <tex>\mathtt{elt}(x)</tex>. | ||
| + | |||
| + | ====Пример==== | ||
''' Первый блок ''' | ''' Первый блок ''' | ||
| − | Так как очередь <tex>B</tex> в начале пуста, то <tex>\mathtt{merged}=C_1^s</tex>. Присвоим ключи | + | Так как очередь <tex>B</tex> в начале пуста, то <tex>\mathtt{merged}=C_1^s</tex>. Присвоим ключи элементам в списке <tex>\mathtt{merged}</tex> как их индексы в этом списке. Восстанавливаем последовательность ключей элементов в порядке исходной последовательности, действуя перестановкой смещений <tex>\xi_1</tex> на последовательность ключей в отсортированном блоке. |
| − | {| | + | {| |
| || | | || | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
| Строка 290: | Строка 291: | ||
| <tex>1</tex>||<tex>2</tex>||<tex>5</tex>||<tex>6</tex>||<tex>12</tex> | | <tex>1</tex>||<tex>2</tex>||<tex>5</tex>||<tex>6</tex>||<tex>12</tex> | ||
|} | |} | ||
| + | |} | ||
| + | |||
| + | {| | ||
| || | | || | ||
{| class="wikitable" style="center" | {| class="wikitable" style="center" | ||
| Строка 298: | Строка 302: | ||
|-align="center" | |-align="center" | ||
|<tex>key</tex>||<tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>4</tex>||<tex>5</tex>||<tex>6</tex>||<tex>7</tex>||<tex>8</tex> | |<tex>key</tex>||<tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>4</tex>||<tex>5</tex>||<tex>6</tex>||<tex>7</tex>||<tex>8</tex> | ||
| + | |} | ||
| + | | || | ||
| + | {| class="wikitable" style="center" | ||
| + | |-align="center" | ||
| + | | colspan="3"|<tex>\mathtt{ind_1}</tex> | ||
| + | |-align="center" | ||
| + | | <tex>3</tex>||<tex>4</tex>||<tex>7</tex> | ||
| + | |} | ||
| + | | || | ||
| + | {| class="wikitable" style="center" | ||
| + | |-align="center" | ||
| + | | colspan="5"|<tex>\mathtt{ind_0}</tex> | ||
| + | |-align="center" | ||
| + | | <tex>1</tex>||<tex>2</tex>||<tex>5</tex>||<tex>6</tex>||<tex>8</tex> | ||
|} | |} | ||
|} | |} | ||
| Строка 306: | Строка 324: | ||
| || | | || | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
| − | ! colspan="6"| | + | ! colspan="6"|Сортированный |
|- | |- | ||
| <tex>\pi</tex> ||<tex>1</tex>||<tex>2</tex>||<tex>5</tex>||<tex>6</tex>||<tex>12</tex> | | <tex>\pi</tex> ||<tex>1</tex>||<tex>2</tex>||<tex>5</tex>||<tex>6</tex>||<tex>12</tex> | ||
| Строка 326: | Строка 344: | ||
Обновляем ключи в очереди: | Обновляем ключи в очереди: | ||
{| class="wikitable" style="center" style="background: #ffffcc" | {| class="wikitable" style="center" style="background: #ffffcc" | ||
| − | ! <tex>B_1</tex>||<tex>B_2</tex>||<tex>B_3</tex>||<tex> | + | ! <tex>B_1</tex>||<tex>B_2</tex>||<tex>B_3</tex>||<tex>key</tex> |
|-align="center" | |-align="center" | ||
| style="background:#FFC9C9"| <tex>3</tex> || || || style="background: #CFCFFF"| <tex>3</tex> | | style="background:#FFC9C9"| <tex>3</tex> || || || style="background: #CFCFFF"| <tex>3</tex> | ||
| Строка 377: | Строка 395: | ||
| <tex>7</tex>||<tex>11</tex> | | <tex>7</tex>||<tex>11</tex> | ||
|} | |} | ||
| + | |} | ||
| + | |||
| + | {| | ||
| || | | || | ||
{| class="wikitable" style="center" | {| class="wikitable" style="center" | ||
| Строка 385: | Строка 406: | ||
|-align="center" | |-align="center" | ||
|<tex>key</tex>||<tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>4</tex>||<tex>5</tex>||<tex>6</tex> | |<tex>key</tex>||<tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>4</tex>||<tex>5</tex>||<tex>6</tex> | ||
| + | |} | ||
| + | | || | ||
| + | {| class="wikitable" style="center" | ||
| + | |-align="center" | ||
| + | | colspan="4"|<tex>\mathtt{ind_1}</tex> | ||
| + | |-align="center" | ||
| + | | <tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>6</tex> | ||
| + | |} | ||
| + | | || | ||
| + | {| class="wikitable" style="center" | ||
| + | |-align="center" | ||
| + | | colspan="2"|<tex>\mathtt{ind_0}</tex> | ||
| + | |-align="center" | ||
| + | | <tex>4</tex>||<tex>5</tex> | ||
|} | |} | ||
|} | |} | ||
| Строка 415: | Строка 450: | ||
Обновление старых ключей: | Обновление старых ключей: | ||
{| class="wikitable" style="center" style="background: #ffffcc" | {| class="wikitable" style="center" style="background: #ffffcc" | ||
| − | ! <tex>B_1</tex>||<tex>B_2</tex>||<tex>B_3</tex>||<tex>B_4</tex>||<tex> | + | ! <tex>B_1</tex>||<tex>B_2</tex>||<tex>B_3</tex>||<tex>B_4</tex>||<tex>key</tex> |
|-align="center" | |-align="center" | ||
| style="background:#FFC9C9"| <tex>1</tex> || || || || style="background: #CFCFFF"| <tex>1</tex> | | style="background:#FFC9C9"| <tex>1</tex> || || || || style="background: #CFCFFF"| <tex>1</tex> | ||
Текущая версия на 21:42, 19 января 2018
| Задача: |
| Дана перестановка множества . Требуется найти НВП за , где — длина НВП. |
Содержание
Алгоритм за O(n log log n)
Нахождение длины НВП
Основная идея
Пусть — входная перестановка.
Будем последовательно обрабатывать элементы в порядке
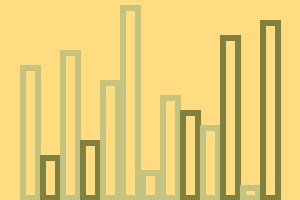
Для каждой длины предполагаемой НВП находим наименьший элемент, который может быть последним в возрастающей подпоследовательности длины и запишем его в массив . Будем называть его наилучшим элементом для длины .
- Если больше каждого элемента , вычисленного для подпоследовательности , тогда с ним можно сделать возрастающую подпоследовательность максимальной длины из уже рассмотренных, в которой он будет последним элементом. Значит, записываем его в конец .
- Иначе будет наилучшим элементом для уже существующей длины и сможет улучшить только один элемент в , тогда мы находим наименьшее и заменяем элементом .
Следует отметить, что полученный массив также образует возрастающую последовательность, на котором мы должны выполнять операции , соответственно целесообразно использовать приоритетную очередь, реализованную через Дерево ван Эмде Боаса. Так как данная структура данных производит описанные операции за , где k — количество бит чисел, которые позволяет хранить дерево, то полученный алгоритм работает за , потому что все элементы последовательности не превосходят n.
Пример
Типы операций
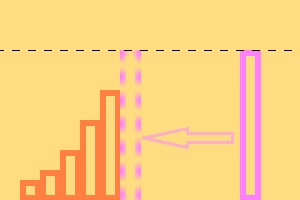
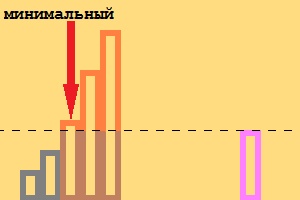
- Добавление элемента, который больше всех предыдущих:
- Замещение элемента более подходящим, т.е. добавление немаксимального элемента:
Пример последовательности
Состояние очереди при каждом добавлении
Псевдокод
int LIS([n]) PriorityQueue B // рабочая приоритетная очередь int k = 0 // длина НВП for i = 1 to n x = [i] // в любом случае добавляем в очередь очередной элемент // устаревшие будем удалять B.insert(x) if B.next(x) // добавленный элемент — не максимальный // удаляем следующее за x значение B.delete(B.next(x)) else // добавленный элемент — максимальный // предыдущие значения не трогаем, очередь увеличилась k = k + 1 return k
Расширение алгоритма до нахождения НВП
Основная идея
Будем запоминать пары: для каждого элемента записываем его "предшественника".
Тогда, пройдя по предшественникам, начиная с последнего элемента очереди , мы можем восстановить НВП.
Общий вид алгоритма
| predecessor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Псевдокод
int[] LIS([n]) PriorityQueue B int k = 0 int predecessor[n] // резервируем позиций for i = 1 to n x = [i] B.insert(x) predecessor[x] = B.prev(x) if B.next(x) B.delete(B.next(x)) else k = k + 1 // по цепочке от последнего элемента // восстанавливаем НВП int result[k] int cur = B.max for i = k - 1 downto 0 result[i] = cur cur = predecessor[cur] return result
Оптимизация до O(n log log k)
Основная идея
Чтобы Дерево ван Эмде Боаса выполняло операции за , необходимо алфавит обрабатываемых значений уменьшить до .
Предположим, мы знаем такое приближение числа числом . Мы обсудим, как найти такое позже.
Во время обработки ключей элементов описанный выше алгоритм работает только с очередью и не зависит от предыдущих элементов последовательности, которые не находятся в очереди. Поэтому, если мы разобьем всю последовательность на блоки из элементов (последний блок может быть меньше), и нам удастся обрабатывать каждый как перестановку из элементов, сохраняя очередь для вычисленных ранее блоков, то мы получим асимптотическое время , а так как , то . (Мы будем обрабатывать блоки последовательно, т.е. с предыдущего блока у нас может остаться значений в очереди, которые дополняются значениями очередного блока — получаем верхнее ограничение в обрабатываемых возможных значений.)
Деление на блоки
Последовательность делится на блоки :
Обозначим за отсортированный блок . Отсортированные и неотсортированные блоки будем хранить в памяти.
Цифровая сортировка каждого блока отдельно будет давать нам время работы . Дополним каждый элемент номером блока, в котором он находится и смещением в этом блоке. Теперь, рассматривая номер блока как старший разряд, элемент как младший разряд (по смещению внутри блока не сортируем), можно сортировать цифровой сортировкой за линейное время , потому что значения элементов и номера блоков не превосходят .
Перестановка смещений, образованная в сортированном блоке есть не что иное, как обратная перестановка перестановки , элементы которой соотносятся между собой как элементы исходного блока. Т.е. если элемент находится в исходной перестановке в блоке на позиции , то в блоке он на позиции .
Пример
Предположим, что . Исходно получаем:
| Блок | ||||||||||||
| Смещение |
После сортировки:
| Блок | ||||||||||||
| Смещение |
Обратные перестановки ():
Обработка блока
Обрабатывая блок, каждому элементу внутри этого блока взаимно однозначно сопоставим ключ так, чтобы их значения находились в промежутке . Очередь будет работать непосредственно с ключами элементов.
Работая с блоком , будем сливать элементы, ключи которых находятся в очереди , с в список . Поскольку мы предположили, что , то количество ключей в не больше , тогда длина не больше , что позволяет однозначно определить ключи на множестве . Как было замечено ранее, элементы, чьи ключи находятся в , располагаются в возрастающем порядке, поэтому возможно производить тривиальную операцию слияния за .
В итоге, получим отсортированный список . Сопоставим ключ каждому элементу как его позицию в этом списке, тогда справедливы утверждения, что и , где , поэтому любая возрастающая последовательность ключей элементов будет соответствовать возрастающей последовательности элементов. Таким образом, приоритетная очередь сможет корректно работать с ключами элементов.
Находим последовательность ключей, соответствующую элементам блока . Действуя на эту последовательность перестановкой , получаем последовательность ключей в порядке исходного блока.
Оставшиеся ключи, которые входят в , но не являются ключами элементов в обрабатываемом блоке, будут ключами элементов из очереди . Обновляем очередь этими ключами.
Затем запускаем алгоритм , для ключей элементов в порядке исходной последовательности.
В итоге, обработка блока делится на следующие этапы:
- Достаем из очереди ключи , конвертируем их в элементы и кладём в список .
- Сливаем элементы в со следующим отсортированным блоком в список , генерируя два вспомогательных массива и , хранящих индексы элементов списков и соответственно в списке .
- Действуя на последовательность ключей в списке перестановкой получим ключи в порядке исходной последовательности.
- Вставляем в новые ключи элементов списка (элементы ).
- Обрабатываем ключи элементов блока в порядке исходной последовательности с помощью алгоритма . Для восстановления НВП также используем массив "предшественников", который будет работать с соответствующими ключам элементами .
Пример
Первый блок
Так как очередь в начале пуста, то . Присвоим ключи элементам в списке как их индексы в этом списке. Восстанавливаем последовательность ключей элементов в порядке исходной последовательности, действуя перестановкой смещений на последовательность ключей в отсортированном блоке.
|
| ||||||||||||||||||||||||||||||||||||||||||||
Обработка блока с помощью алгоритма .
В результате получаем
Второй блок
Восстанавливаем элементы из : .
Сливаем и восстановленные элементы из в и присваиваем элементам ключи как индексы элементов в полученном списке:
|
|
| ||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||
Получаем ключи элементов в и находим перестановку ключей в порядке исходной последовательности, действуя перестановкой :
|
| ||||||||||||||||||||||||||||||||||||||||||||
Обновляем ключи в очереди:
запускаем для блока:
В результате получаем:
Третий блок
Восстанавливаем элементы из : .
Сливаем и восстановленные элементы из и присваиваем ключи элементам:
|
|
| ||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||
Получаем ключи элементов в и находим перестановку ключей в порядке исходной последовательности, действуя перестановкой :
Обновление старых ключей: запускаем для блока: Результат завершения алгоритма:
Получаем, что длина НВП — , и НВП оканчивается на . Восстановление НВП Начинаем восстановление с :
Нахождение размера блоковРассмотрим последовательность , где , — некоторое значение, меньшее . Будем последовательно для элементов этой последовательности запускать алгоритм, представленный выше. Если размер очереди становится больше , то условие перестает выполняться, тогда останавливаем алгоритм и переходим к следующему значению . Для каждого размер списка не больше , а количество блоков всего . То общее количество присваиваний новых ключей элементам последовательности, также как и количество операций слияния списков, не больше , где c — некоторая константа. Каждая операция с приоритетной очередью требует времени, так как элементы в не больше . Таким образом, время работы запущенного алгоритма для каждого — . Когда найдётся первое , то алгоритм успешно завершится. .
Общее время работы алгоритма для всех обработанных значений — . Заметим, что , так как в противном случае , что противоречит тому, что — первый из тех, которые больше . Следовательно, . Получаем время работы . См. также
Источники информации |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||