Модель алгоритма и её выбор — различия между версиями
(Исправлены замечания) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 54 промежуточные версии 10 участников) | |||
| Строка 2: | Строка 2: | ||
Пусть дана обучающая выборка <tex>(X, Y)</tex>, где <tex> X </tex> {{---}} множество признаков, описывающих объекты, а <tex> Y </tex> {{---}} конечное множество меток. | Пусть дана обучающая выборка <tex>(X, Y)</tex>, где <tex> X </tex> {{---}} множество признаков, описывающих объекты, а <tex> Y </tex> {{---}} конечное множество меток. | ||
| − | Пусть | + | Пусть задана функция <tex> g: X \times \Theta \rightarrow Y </tex>, где <tex> \Theta </tex> {{---}} множество дополнительных параметров (весов) функции. |
| − | + | Описанная выше функция <tex> g </tex> для фиксированного значения весов <tex> \theta \in \Theta </tex> называется '''решающим правилом'''. | |
| − | + | '''Модель''' {{---}} совокупность всех решающих правил, которые получаются путем присваивания весам всех возможных допустимых значений. | |
| − | + | Формально модель <tex> A = \{g(x, \theta) | \theta \in \Theta\} </tex>. | |
| − | + | Модель определяется множеством допустимых весов <tex> \Theta </tex> и структурой решающего правила <tex> g(x,\theta) </tex>. | |
| − | + | === Понятие гиперпараметров модели === | |
| + | '''Гиперпараметры модели''' {{---}} параметры, значения которых задается до начала обучения модели и не изменяется в процессе обучения. У модели может не быть гиперпараметров. | ||
| − | + | '''Параметры модели''' {{---}} параметры, которые изменяются и оптимизируются в процессе обучения модели и итоговые значения этих параметров являются результатом обучения модели. | |
| − | ''' | ||
| − | + | Примерами гиперпараметров могут служить количество слоев нейронной сети, а также количество нейронов на каждом слое. Примерами параметров могут служить веса ребер нейронной сети. | |
| + | |||
| + | Для нахождения оптимальных гиперпараметров модели могут применяться различные алгоритмы [[Настройка гиперпараметров | настройки гиперпараметров]]<sup>[на 28.01.19 не создан]</sup>. | ||
| + | |||
| + | === Пример === | ||
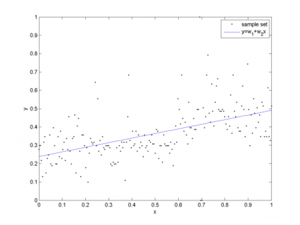
| + | [[Файл:Linear-regression.png|300px|thumb|[http://www.machinelearning.ru/wiki/index.php?title=%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29 Рис 1. Пример линейной регрессии]]] | ||
| + | В качестве примера модели приведем [[Линейная регрессия | линейную регрессию]]. | ||
| + | |||
| + | Линейная регрессия задается следующей формулой: | ||
| + | |||
| + | <tex> g(x, \theta) = \theta_0 + \theta_1x_1 + ... + \theta_kx_k = \theta_0 + \sum_{i=1}^k \theta_ix_i = \theta_0 + x^T\theta</tex>, где <tex> x^T = (x_1, x_2, ..., x_k) </tex> {{---}} вектор признаков, | ||
| + | |||
| + | <tex> \theta = (\theta_1, \theta_2, ..., \theta_k)</tex> {{---}} веса модели, настраиваемые в процессе обучения. | ||
| − | + | Гиперпараметром модели является число слагаемых в функции <tex> g(x, \theta) </tex>. | |
| − | + | Более подробный пример линейной регрессии можно посмотреть в статье [[Переобучение | переобучение]]. | |
== Задача выбора модели == | == Задача выбора модели == | ||
| − | Пусть <tex> A </tex> {{---}} модель алгоритма, характеризующаяся гиперпараметрами <tex> \lambda = \{\lambda_1, ..., \lambda_m\}, \lambda_1 \in \Lambda_1, ..., \lambda_m \in \Lambda_m </tex>. Тогда с ней связано пространство гиперпараметров <tex> \Lambda = \Lambda_1 \times ... \times \Lambda_m </tex>. За <tex> A_{\lambda}</tex> обозначим алгоритм, то есть модель алгоритма, для которой задан вектор гиперпараметров <tex> \lambda \in \Lambda </tex>. | + | Пусть <tex> A </tex> {{---}} модель алгоритма, характеризующаяся гиперпараметрами <tex> \lambda = \{\lambda_1, ..., \lambda_m\}, \lambda_1 \in \Lambda_1, ..., \lambda_m \in \Lambda_m </tex>. Тогда с ней связано пространство гиперпараметров <tex> \Lambda = \Lambda_1 \times ... \times \Lambda_m </tex>. |
| + | |||
| + | За <tex> A_{\lambda}</tex> обозначим алгоритм, то есть модель алгоритма, для которой задан вектор гиперпараметров <tex> \lambda \in \Lambda </tex>. | ||
Для выбора наилучшего алгоритма необходимо зафиксировать меру качества работы алгоритма. Назовем эту меру <tex> Q(A_{\lambda}, D) </tex>. | Для выбора наилучшего алгоритма необходимо зафиксировать меру качества работы алгоритма. Назовем эту меру <tex> Q(A_{\lambda}, D) </tex>. | ||
| Строка 31: | Строка 45: | ||
==== Подзадача выбора лучшего алгоритма из портфолио ==== | ==== Подзадача выбора лучшего алгоритма из портфолио ==== | ||
| − | Дано некоторое множество алгоритмов с фиксированными структурными параметрами <tex> \mathcal{A} = \{A^1_{\lambda_1}, ..., A^m_{\lambda_m}\}</tex> и обучающая выборка <tex> D = \{d_1, ..., d_n\}</tex>. Здесь <tex> d_i = (x_i, y_i) \in (X, Y)</tex>. Требуется выбрать алгоритм <tex> A^*_{\lambda_*} </tex>, который окажется наиболее эффективным с точки зрения меры качества <tex> Q </tex> | + | Дано некоторое множество алгоритмов с фиксированными структурными параметрами <tex> \mathcal{A} = \{A^1_{\lambda_1}, ..., A^m_{\lambda_m}\}</tex> и обучающая выборка <tex> D = \{d_1, ..., d_n\}</tex>. Здесь <tex> d_i = (x_i, y_i) \in (X, Y)</tex>. Требуется выбрать алгоритм <tex> A^*_{\lambda_*} </tex>, который окажется наиболее эффективным с точки зрения меры качества <tex> Q </tex>. |
==== Подзадача оптимизации гиперпараметров ==== | ==== Подзадача оптимизации гиперпараметров ==== | ||
Подзадача оптимизации гиперпараметров заключается в подборе таких <tex> \lambda^* \in \Lambda </tex>, при которых заданная модель алгоритма <tex> A </tex> будет наиболее эффективна. | Подзадача оптимизации гиперпараметров заключается в подборе таких <tex> \lambda^* \in \Lambda </tex>, при которых заданная модель алгоритма <tex> A </tex> будет наиболее эффективна. | ||
| Строка 38: | Строка 52: | ||
=== Методы выбора модели === | === Методы выбора модели === | ||
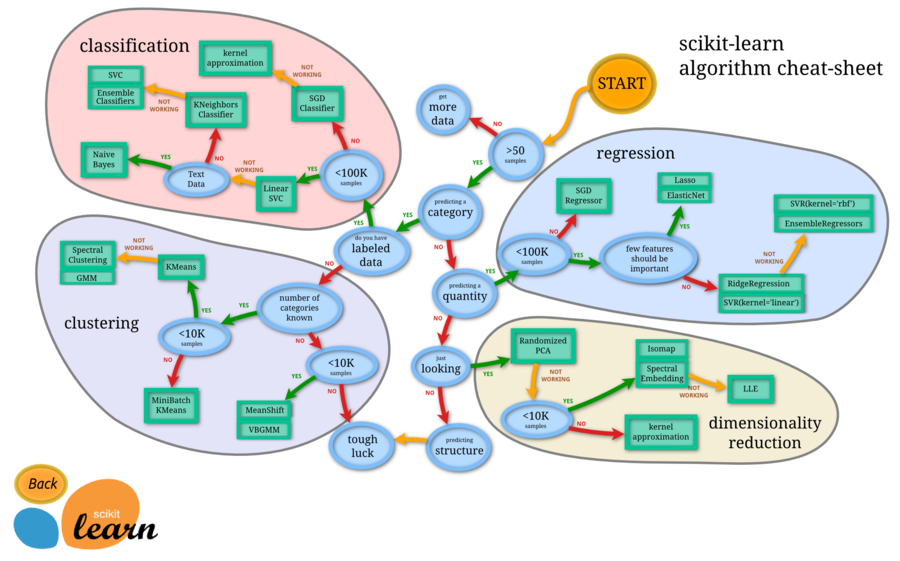
| − | + | Модель можно выбрать из некоторого множества моделей, проверив результат работы каждой модели из множества с помощью ручного тестирования, но ручное тестирование серьезно ограничивает количество моделей, которые можно перебрать, а также требует больших трудозатрат. Поэтому в большинстве случаев используются алгоритмы, позволяющие автоматически выбирать модель. Далее будут рассмотрены некоторые из таких алгоритмов. | |
| + | [[Файл:Scikit-learn-scheme.png|900px|thumb|center|[https://www.codeastar.com/choose-machine-learning-models-python/ Рис 2. Схема выбора модели в библиотеке scikit-learn для Python]]] | ||
| + | ==== Кросс-валидация ==== | ||
| + | {{main|Кросс-валидация}} | ||
| − | + | Основная идея алгоритма кросс-валидации {{---}} разбить обучающую выборку на обучающую и тестовую. Таким образом, будет возможным эмулировать наличие тестовой выборки, не участвующей в обучении, но для которой известны правильные ответы. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Таким образом | ||
Достоинства и недостатки кросс-валидации: | Достоинства и недостатки кросс-валидации: | ||
| Строка 55: | Строка 65: | ||
==== Мета-обучение ==== | ==== Мета-обучение ==== | ||
| − | Целью мета-обучения является решение задачи выбора алгоритма из портфолио алгоритмов для решения поставленной задачи без непосредственного применения каждого из них. Решение этой задачи в рамках мета-обучения сводится к задаче обучения с учителем. Для этого используется заранее отобранное множество наборов данных <tex> D </tex>. Для каждого набора данных <tex> d \in D </tex> вычисляется вектор мета-признаков, которые описывают свойства этого набора данных. Ими могут быть: число категориальных или численных признаков | + | {{main|Мета-обучение}} |
| + | |||
| + | Целью мета-обучения является решение задачи выбора алгоритма из портфолио алгоритмов для решения поставленной задачи без непосредственного применения каждого из них. Решение этой задачи в рамках мета-обучения сводится к задаче [https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81_%D1%83%D1%87%D0%B8%D1%82%D0%B5%D0%BB%D0%B5%D0%BC обучения с учителем]. Для этого используется заранее отобранное множество наборов данных <tex> D </tex>. Для каждого набора данных <tex> d \in D </tex> вычисляется вектор мета-признаков, которые описывают свойства этого набора данных. Ими могут быть: число категориальных или численных признаков объектов в <tex> d </tex>, число возможных меток, размер <tex> d </tex> и многие другие<ref>[https://www.fruct.org/publications/ainl-fruct/files/Fil.pdf Datasets meta-feature description for recommending feature selection algorithm]</ref>. Каждый алгоритм запускается на всех наборах данных из <tex> D </tex>. После этого вычисляется эмпирический риск, на основе которого формируются метки классов. Затем мета-классификатор обучается на полученных результатах. В качестве описания набора данных выступает вектор мета-признаков, а в качестве метки — алгоритм, оказавшийся самым эффективным с точки зрения заранее выбранной меры качества. | ||
Достоинства и недостатки мета-обучения: | Достоинства и недостатки мета-обучения: | ||
| Строка 61: | Строка 73: | ||
# Точность алгоритма может быть ниже, чем при кросс-валидации. | # Точность алгоритма может быть ниже, чем при кросс-валидации. | ||
| − | ==== Теория Вапника- | + | ====[http://www.machinelearning.ru/wiki/index.php?title=%D0%A0%D0%B0%D0%B7%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%92%D0%B0%D0%BF%D0%BD%D0%B8%D0%BA%D0%B0-%D0%A7%D0%B5%D1%80%D0%B2%D0%BE%D0%BD%D0%B5%D0%BD%D0%BA%D0%B8%D1%81%D0%B0 Теория Вапника-Червоненкинса] ==== |
Идея данной теории заключается в следующем: чем более «гибкой» является модель, тем хуже ее обобщающая способность. Данная идея базируется на том, что «гибкое» решающее правило способно настраиваться на малейшие шумы, содержащиеся в обучающей выборке. | Идея данной теории заключается в следующем: чем более «гибкой» является модель, тем хуже ее обобщающая способность. Данная идея базируется на том, что «гибкое» решающее правило способно настраиваться на малейшие шумы, содержащиеся в обучающей выборке. | ||
| Строка 70: | Строка 82: | ||
Очевидно, что чем больше емкость, тем более «гибкой» является модель и, соответственно, тем хуже. Значит нужно добиваться минимально возможного количества ошибок на обучении при минимальной возможной емкости. | Очевидно, что чем больше емкость, тем более «гибкой» является модель и, соответственно, тем хуже. Значит нужно добиваться минимально возможного количества ошибок на обучении при минимальной возможной емкости. | ||
| − | Существует формула Вапника, связывающая ошибку на обучении <tex> P_{train}( | + | Существует формула Вапника, связывающая ошибку на обучении <tex> P_{train}(\theta) </tex>, емкость <tex> h(\theta) </tex> и ошибку на генеральной совокупности <tex> P_{test}(\theta) </tex>: |
| − | <tex> P_{test}( | + | <tex> P_{test}(\theta) <= P_{train}(\theta) + \sqrt{\frac{h(\Theta) * (\log{(\frac{2d}{h(\Theta)})} + 1) - \log{(\frac{\eta}{4})}}{n}} </tex>, где <tex> d </tex> {{---}} размерность пространства признаков. |
| − | Неравенство верно с вероятностью <tex> 1 - \eta </tex> <tex> \forall | + | Неравенство верно с вероятностью <tex> 1 - \eta </tex> <tex> \forall \theta \in \Theta </tex>. |
| − | Алгоритм выбора модели согласно теории Вапника-Червоненкиса: | + | Алгоритм выбора модели согласно теории Вапника-Червоненкиса: последовательно анализируя модели с увеличивающейся емкостью, необходимо выбирать модель с наименьшей верхней оценкой тестовой ошибки. |
Достоинства теории Вапника-Червоненкиса: | Достоинства теории Вапника-Червоненкиса: | ||
| Строка 85: | Строка 97: | ||
# Для большинства моделей емкость не поддается оценке; | # Для большинства моделей емкость не поддается оценке; | ||
# Многие модели с бесконечной емкостью показывают хорошие результаты на практике. | # Многие модели с бесконечной емкостью показывают хорошие результаты на практике. | ||
| + | |||
| + | == Существующие системы автоматического выбора модели == | ||
| + | ===Автоматизированный выбор модели в библиотеке [https://www.ml4aad.org/wp-content/uploads/2018/07/automl_book_draft_auto-weka.pdf auto-WEKA] для Java=== | ||
| + | Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задач классификации и регрессии (начиная с версии 2.0). | ||
| + | |||
| + | Библиотека позволяет автоматически выбирать из 27 базовых алгоритмов, 10 мета-алгоритмов и 2 ансамблевых алгоритмов лучший, одновременно настраивая его гиперпараметры при помощи алгоритма [https://www.ml4aad.org/automated-algorithm-design/algorithm-configuration/smac/ SMAC]. Решение достигается полным перебором: оптимизация гиперпараметров запускается на всех алгоритмах по очереди. Недостатком такого подхода является слишком большое время выбора модели. | ||
| + | ===Автоматизированный выбор модели в библиотеке [https://epistasislab.github.io/tpot/ Tree-base Pipeline Optimization Tool (TPOT)] для Python.=== | ||
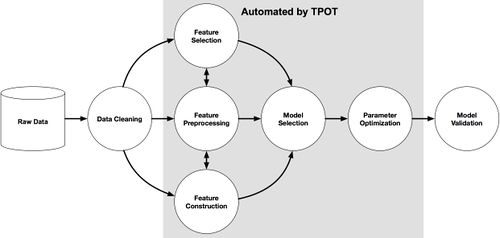
| + | [[Файл:TPOT-scheme.jpeg|500px|thumb|[https://raw.githubusercontent.com/EpistasisLab/tpot/master/images/tpot-ml-pipeline.png Рис 3. Схема выбора модели в библиотеке TPOT]]] | ||
| + | Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации. | ||
| + | |||
| + | Выбор модели осуществляется на основе конвейера, организованного в древовидной структуре. Каждая вершина дерева {{---}} один из четырех операторов конвейера (preprocessing, decomposition, feature selection, modeling). Каждый конвейер начинается с одной или нескольких копий входного набора данных, которые являются листьями дерева и которые подаются в операторы в соответствии со структурой конвейера. Данные модифицируются оператором в вершине и поступают на вход следующей вершины. В библиотеке используются генетические алгоритмы для нахождения лучших конвейеров. | ||
| + | |||
| + | После создания конвеера, оценивается его производительность и случайным образом изменяются части конвеера для поиска наибольшей эффективности. Время работы TPOT может варьироваться в зависимости от размера входных данных. При начальных настройках в 100 поколений с размером популяции 100, за время работы оценивается 10000 конфигураций конвеера. По времени это сравнимо с [https://en.wikipedia.org/wiki/Hyperparameter_optimization#Grid_search поиском по сетке] для 10000 комбинаций гиперпараметров. Это 10000 конфигураций модели со [[Кросс-валидация | скользящим контролем]] по 10 блокам, что означает, что около 100000 моделей создается и оценивается на обучающих данных в одном поиске по сетке. Поэтому, для некоторых наборов данных требуется всего несколько минут, чтобы найти высокопроизводительную модель для работы, а некоторым может потребоваться несколько дней. | ||
| + | |||
| + | После поиска конвейера его также можно экспортировать в файл Python. | ||
| + | |||
| + | ===Автоматизированный выбор модели в библиотеке [https://automl.github.io/auto-sklearn/stable/ auto-sklearn] для Python=== | ||
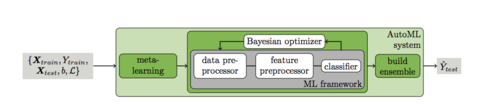
| + | [[Файл:Auto-sklearn-scheme.png|500px|thumb|[https://papers.nips.cc/paper/5872-efficient-and-robust-automated-machine-learning.pdf Рис 4. Схема выбора модели в библиотеке auto-sklearn]]] | ||
| + | Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации. | ||
| + | |||
| + | Сначала используется мета-обучение на основе различных признаков и мета-признаков набора данных, чтобы найти наилучшие модели. После этого используется подход [https://en.wikipedia.org/wiki/Bayesian_optimization Байесовской оптимизации], чтобы найти наилучшие гиперпараметры для наилучших моделей. | ||
| + | |||
| + | На рисунке 5 показаны общие компоненты Auto-sklearn. Он состоит из 15 алгоритмов классификации, 14 методов предварительной обработки и 4 методов предварительной обработки данных. Мы параметризовали каждый из них, что привело к пространству, состоящему из 110 гиперпараметров. Большинство из них являются условными гиперпараметрами, которые активны, только если выбран соответствующий компонент. Отметим, что SMAC может обрабатывать эту обусловленность изначально. | ||
| + | |||
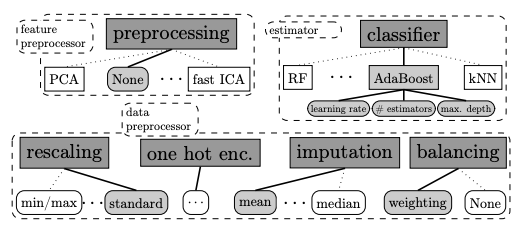
| + | [[Файл:model_5.png|900px|center|thumb| Рис 5. Структурированное пространство конфигурации. Квадратные прямоугольники обозначают родительские гиперпараметры, прямоугольники с закругленными краями являются листовыми гиперпараметрами. Серые прямоугольники отмечают активные гиперпараметры, которые образуют пример конфигурации и конвейера машинного обучения. Каждый конвейер содержит один препроцессор, классификатор и до трех методов препроцессора данных, а также соответствующие гиперпараметры.]] | ||
== См. также == | == См. также == | ||
| − | * [[Настройка гиперпараметров]]<sup>[на | + | * [[Настройка гиперпараметров]]<sup>[на 28.01.19 не создан]</sup> |
* [[Переобучение]] | * [[Переобучение]] | ||
| − | * [[Мета-обучение]] | + | * [[Мета-обучение]] |
| + | * [[Линейная регрессия]] | ||
== Примечания == | == Примечания == | ||
| − | + | <references/> | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Источники информации == | == Источники информации == | ||
| − | + | * [http://www.machinelearning.ru/wiki/images/0/05/BMMO11_4.pdf machinelearning.ru {{---}} Задачи выбора модели] | |
| − | + | * [https://en.wikipedia.org/wiki/Hyperparameter_(machine_learning) Wikipedia {{---}} Hyperparameter] | |
| − | + | * [https://machinelearningmastery.com/difference-between-a-parameter-and-a-hyperparameter/ What is the Difference Between a Parameter and a Hyperparameter?] | |
| − | + | * [http://jmlda.org/papers/doc/2016/no2/Efimova2016Reinforcement.pdf Применение обучения с подкреплением для одновременного выбора модели алгоритма классификации и ее структурных параметров] | |
| + | * [https://7bce9816-a-62cb3a1a-s-sites.googlegroups.com/site/automl2017icml/accepted-papers/AutoML_2017_paper_23.pdf?attachauth=ANoY7cr6uPaUoNh3gc3A-A1UbLXQgNEATEkfZmKD8kozB3hpCYtM9JwnOevEsW9W42CwurzJKrxxEatcB4DCjWNB_Ndvy1uC0lbQyCTlDIfrW6eYJXvdbFJPilYfmf8_ryilH0IwG0ddntLYy-VA3Fm1JeM495fTZxorYth0DDKiqtKvSR92dGl8CM_mUB7sun0R6wurCxM36QqcYEaf5kIm13MM0reWlR3aPZVNe_-AefOCpoXznR-wH04mSWjH8jmlk5Bw51AN&attredirects=0 Fast Automated Selection of Learning Algorithm And its Hyperparameters by Reinforcement Learning] | ||
| + | * Shalamov V., Efimova V., Muravyov S., and Filchenkov A. "Reinforcement-based Method for Simultaneous Clustering Algorithm Selection and its Hyperparameters Optimization." Procedia Computer Science 136 (2018): 144-153. | ||
| + | |||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
| − | |||
| − | |||
Текущая версия на 19:19, 4 сентября 2022
Понятие модели
Пусть дана обучающая выборка , где — множество признаков, описывающих объекты, а — конечное множество меток.
Пусть задана функция , где — множество дополнительных параметров (весов) функции.
Описанная выше функция для фиксированного значения весов называется решающим правилом.
Модель — совокупность всех решающих правил, которые получаются путем присваивания весам всех возможных допустимых значений.
Формально модель .
Модель определяется множеством допустимых весов и структурой решающего правила .
Понятие гиперпараметров модели
Гиперпараметры модели — параметры, значения которых задается до начала обучения модели и не изменяется в процессе обучения. У модели может не быть гиперпараметров.
Параметры модели — параметры, которые изменяются и оптимизируются в процессе обучения модели и итоговые значения этих параметров являются результатом обучения модели.
Примерами гиперпараметров могут служить количество слоев нейронной сети, а также количество нейронов на каждом слое. Примерами параметров могут служить веса ребер нейронной сети.
Для нахождения оптимальных гиперпараметров модели могут применяться различные алгоритмы настройки гиперпараметров[на 28.01.19 не создан].
Пример
В качестве примера модели приведем линейную регрессию.
Линейная регрессия задается следующей формулой:
, где — вектор признаков,
— веса модели, настраиваемые в процессе обучения.
Гиперпараметром модели является число слагаемых в функции .
Более подробный пример линейной регрессии можно посмотреть в статье переобучение.
Задача выбора модели
Пусть — модель алгоритма, характеризующаяся гиперпараметрами . Тогда с ней связано пространство гиперпараметров .
За обозначим алгоритм, то есть модель алгоритма, для которой задан вектор гиперпараметров .
Для выбора наилучшего алгоритма необходимо зафиксировать меру качества работы алгоритма. Назовем эту меру .
Задачу выбора наилучшего алгоритма можно разбить на две подзадачи: подзадачу выбора лучшего алгоритма из портфолио и подзадачу настройки гиперпараметров.
Подзадача выбора лучшего алгоритма из портфолио
Дано некоторое множество алгоритмов с фиксированными структурными параметрами и обучающая выборка . Здесь . Требуется выбрать алгоритм , который окажется наиболее эффективным с точки зрения меры качества .
Подзадача оптимизации гиперпараметров
Подзадача оптимизации гиперпараметров заключается в подборе таких , при которых заданная модель алгоритма будет наиболее эффективна.
Гиперпараметры могут выбираться из ограниченного множества или с помощью перебора из неограниченного множества гиперпараметров, это зависит от непосредственной задачи. Во втором случае актуален вопрос максимального времени, которое можно потратить на поиск наилучших гиперпараметров, так как чем больше времени происходит перебор, тем лучше гиперпараметры можно найти, но при этом может быть ограничен временной бюджет, из-за чего перебор придется прервать.
Методы выбора модели
Модель можно выбрать из некоторого множества моделей, проверив результат работы каждой модели из множества с помощью ручного тестирования, но ручное тестирование серьезно ограничивает количество моделей, которые можно перебрать, а также требует больших трудозатрат. Поэтому в большинстве случаев используются алгоритмы, позволяющие автоматически выбирать модель. Далее будут рассмотрены некоторые из таких алгоритмов.
Кросс-валидация
Основная идея алгоритма кросс-валидации — разбить обучающую выборку на обучающую и тестовую. Таким образом, будет возможным эмулировать наличие тестовой выборки, не участвующей в обучении, но для которой известны правильные ответы.
Достоинства и недостатки кросс-валидации:
- Ошибка в процедуре кросс-валидации является достаточно точной оценкой ошибки на генеральной совокупности;
- Проведение кросс-валидации требует значительного времени на многократное повторное обучение алгоритмов и применимо лишь для «быстрых» алгоритмов машинного обучения;
- Кросс-валидация плохо применима в задачах кластерного анализа и прогнозирования временных рядов.
Мета-обучение
Целью мета-обучения является решение задачи выбора алгоритма из портфолио алгоритмов для решения поставленной задачи без непосредственного применения каждого из них. Решение этой задачи в рамках мета-обучения сводится к задаче обучения с учителем. Для этого используется заранее отобранное множество наборов данных . Для каждого набора данных вычисляется вектор мета-признаков, которые описывают свойства этого набора данных. Ими могут быть: число категориальных или численных признаков объектов в , число возможных меток, размер и многие другие[1]. Каждый алгоритм запускается на всех наборах данных из . После этого вычисляется эмпирический риск, на основе которого формируются метки классов. Затем мета-классификатор обучается на полученных результатах. В качестве описания набора данных выступает вектор мета-признаков, а в качестве метки — алгоритм, оказавшийся самым эффективным с точки зрения заранее выбранной меры качества.
Достоинства и недостатки мета-обучения:
- Алгоритм, обучающийся большое время, запускается меньшее количество раз, что сокращает время работы;
- Точность алгоритма может быть ниже, чем при кросс-валидации.
Теория Вапника-Червоненкинса
Идея данной теории заключается в следующем: чем более «гибкой» является модель, тем хуже ее обобщающая способность. Данная идея базируется на том, что «гибкое» решающее правило способно настраиваться на малейшие шумы, содержащиеся в обучающей выборке.
Емкость модели для задачи классификации — максимальное число объектов обучающей выборки, для которых при любом их разбиении на классы найдется хотя бы одно решающее правило, безошибочно их классифицирующее.
По аналогии емкость обобщается на другие задачи машинного обучения.
Очевидно, что чем больше емкость, тем более «гибкой» является модель и, соответственно, тем хуже. Значит нужно добиваться минимально возможного количества ошибок на обучении при минимальной возможной емкости.
Существует формула Вапника, связывающая ошибку на обучении , емкость и ошибку на генеральной совокупности :
, где — размерность пространства признаков.
Неравенство верно с вероятностью .
Алгоритм выбора модели согласно теории Вапника-Червоненкиса: последовательно анализируя модели с увеличивающейся емкостью, необходимо выбирать модель с наименьшей верхней оценкой тестовой ошибки.
Достоинства теории Вапника-Червоненкиса:
- Серьезное теоретическое обоснование, связь с ошибкой на генеральной совокупности;
- Теория продолжает развиваться и в наши дни.
Недостатки теории Вапника-Червоненкиса:
- Оценки ошибки на генеральной совокупности сильно завышены;
- Для большинства моделей емкость не поддается оценке;
- Многие модели с бесконечной емкостью показывают хорошие результаты на практике.
Существующие системы автоматического выбора модели
Автоматизированный выбор модели в библиотеке auto-WEKA для Java
Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задач классификации и регрессии (начиная с версии 2.0).
Библиотека позволяет автоматически выбирать из 27 базовых алгоритмов, 10 мета-алгоритмов и 2 ансамблевых алгоритмов лучший, одновременно настраивая его гиперпараметры при помощи алгоритма SMAC. Решение достигается полным перебором: оптимизация гиперпараметров запускается на всех алгоритмах по очереди. Недостатком такого подхода является слишком большое время выбора модели.
Автоматизированный выбор модели в библиотеке Tree-base Pipeline Optimization Tool (TPOT) для Python.
Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации.
Выбор модели осуществляется на основе конвейера, организованного в древовидной структуре. Каждая вершина дерева — один из четырех операторов конвейера (preprocessing, decomposition, feature selection, modeling). Каждый конвейер начинается с одной или нескольких копий входного набора данных, которые являются листьями дерева и которые подаются в операторы в соответствии со структурой конвейера. Данные модифицируются оператором в вершине и поступают на вход следующей вершины. В библиотеке используются генетические алгоритмы для нахождения лучших конвейеров.
После создания конвеера, оценивается его производительность и случайным образом изменяются части конвеера для поиска наибольшей эффективности. Время работы TPOT может варьироваться в зависимости от размера входных данных. При начальных настройках в 100 поколений с размером популяции 100, за время работы оценивается 10000 конфигураций конвеера. По времени это сравнимо с поиском по сетке для 10000 комбинаций гиперпараметров. Это 10000 конфигураций модели со скользящим контролем по 10 блокам, что означает, что около 100000 моделей создается и оценивается на обучающих данных в одном поиске по сетке. Поэтому, для некоторых наборов данных требуется всего несколько минут, чтобы найти высокопроизводительную модель для работы, а некоторым может потребоваться несколько дней.
После поиска конвейера его также можно экспортировать в файл Python.
Автоматизированный выбор модели в библиотеке auto-sklearn для Python
Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации.
Сначала используется мета-обучение на основе различных признаков и мета-признаков набора данных, чтобы найти наилучшие модели. После этого используется подход Байесовской оптимизации, чтобы найти наилучшие гиперпараметры для наилучших моделей.
На рисунке 5 показаны общие компоненты Auto-sklearn. Он состоит из 15 алгоритмов классификации, 14 методов предварительной обработки и 4 методов предварительной обработки данных. Мы параметризовали каждый из них, что привело к пространству, состоящему из 110 гиперпараметров. Большинство из них являются условными гиперпараметрами, которые активны, только если выбран соответствующий компонент. Отметим, что SMAC может обрабатывать эту обусловленность изначально.
См. также
- Настройка гиперпараметров[на 28.01.19 не создан]
- Переобучение
- Мета-обучение
- Линейная регрессия
Примечания
Источники информации
- machinelearning.ru — Задачи выбора модели
- Wikipedia — Hyperparameter
- What is the Difference Between a Parameter and a Hyperparameter?
- Применение обучения с подкреплением для одновременного выбора модели алгоритма классификации и ее структурных параметров
- Fast Automated Selection of Learning Algorithm And its Hyperparameters by Reinforcement Learning
- Shalamov V., Efimova V., Muravyov S., and Filchenkov A. "Reinforcement-based Method for Simultaneous Clustering Algorithm Selection and its Hyperparameters Optimization." Procedia Computer Science 136 (2018): 144-153.