Кросс-валидация — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показана 51 промежуточная версия 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Кросс-валидация''' или '''скользящий контроль''' | + | '''Кросс-валидация''' или '''скользящий контроль''' {{---}} процедура эмпирического оценивания обобщающей способности алгоритмов. |
С помощью кросс-валидации эмулируется наличие тестовой выборки, которая не участвует в обучении, но для которой известны правильные ответы. | С помощью кросс-валидации эмулируется наличие тестовой выборки, которая не участвует в обучении, но для которой известны правильные ответы. | ||
| + | === Определения и обозначения === | ||
| + | Пусть <tex> X </tex> {{---}} множество [[Общие понятия | признаков]], описывающих объекты, а <tex> Y </tex> {{---}} конечное множество меток. | ||
| − | == | + | <tex>T^l = {(x_i, y_i)}_{i=1}^{l}, x_i \in X, y_i \in Y</tex> {{---}} обучающая выборка, |
| − | === | + | <tex>Q</tex> {{---}} мера качества, |
| + | |||
| + | <tex>A</tex> {{---}} [[Модель алгоритма и ее выбор | модель]], | ||
| + | |||
| + | <tex>\mu: (X \times Y)^l \to A, </tex> {{---}} алгоритм обучения. | ||
| + | |||
| + | == Разновидности кросс-валидации == | ||
| + | |||
| + | === Валидация на отложенных данных (Hold-Out Validation) === | ||
Обучающая выборка один раз случайным образом разбивается на две части <tex> T^l = T^t \cup T^{l-t} </tex> | Обучающая выборка один раз случайным образом разбивается на две части <tex> T^l = T^t \cup T^{l-t} </tex> | ||
| + | |||
| + | [[Файл:Hold-out.png|500px]] | ||
| + | |||
После чего решается задача оптимизации: | После чего решается задача оптимизации: | ||
| − | <tex>HO(\mu, T^t, T^{l-t}) = Q(\mu(T^t), T^{l-t}) \to min </tex> | + | <tex>HO(\mu, T^t, T^{l-t}) = Q(\mu(T^t), T^{l-t}) \to min </tex>, |
Метод Hold-out применяется в случаях больших датасетов, т.к. требует меньше вычислительных мощностей по сравнению с другими методами кросс-валидации. | Метод Hold-out применяется в случаях больших датасетов, т.к. требует меньше вычислительных мощностей по сравнению с другими методами кросс-валидации. | ||
Недостатком метода является то, что оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения. | Недостатком метода является то, что оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Полная кросс-валидация (Complete cross-validation) === | |
| − | + | # Выбирается значение <tex>t</tex>; | |
| + | # Выборка разбивается всеми возможными способами на две части <tex> T^l = T^t \cup T^{l-t} </tex>. | ||
| + | |||
| + | [[Файл:CompleteCrossValidation.png|500px]] | ||
| + | |||
<tex>CVV_t = \frac{1}{C_l^{l-t}} | <tex>CVV_t = \frac{1}{C_l^{l-t}} | ||
| − | \displaystyle\sum_{T^l = T^t \cup T^{l-t}} Q(\mu(T^t), T^{l-t}) \to min </tex> | + | \displaystyle\sum_{T^l = T^t \cup T^{l-t}} Q(\mu(T^t), T^{l-t}) \to min </tex>, |
| + | |||
| + | Здесь число разбиений <tex>C_l^{l-t}</tex> становится слишком большим даже при сравнительно малых значениях t, что затрудняет практическое применение данного метода. | ||
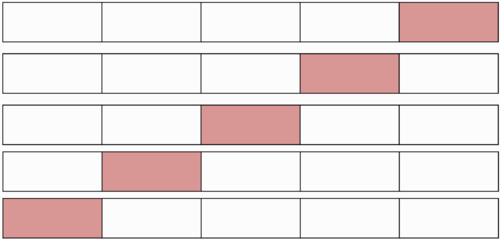
| − | === k-fold | + | === k-fold кросс-валидация === |
| − | # Обучающая выборка разбивается на <tex> k </tex> непересекающихся одинаковых по объему частей | + | # Обучающая выборка разбивается на <tex> k </tex> непересекающихся одинаковых по объему частей; |
# Производится <tex> k </tex> итераций. На каждой итерации происходит следующее: | # Производится <tex> k </tex> итераций. На каждой итерации происходит следующее: | ||
## Модель обучается на <tex> k - 1 </tex> части обучающей выборки; | ## Модель обучается на <tex> k - 1 </tex> части обучающей выборки; | ||
| − | ## Модель тестируется на части обучающей выборки, которая не участвовала в обучении; | + | ## Модель тестируется на части обучающей выборки, которая не участвовала в обучении. |
| + | Каждая из <tex>k</tex> частей единожды используется для тестирования. | ||
| + | Как правило, <tex>k = 10</tex> (5 в случае малого размера выборки). | ||
| + | |||
| + | [[Файл:K-fold-validation.png|500px]] | ||
| + | |||
| + | <tex>T^l = F_1 \cup \dots \cup F_k, |F_i| \approx \frac{l}{k}, | ||
| + | \\ CV_k = \frac{1}{k} \sum_{i=1}^{k} Q(\mu(T^l \setminus F_i),F_i) \to min </tex>. | ||
| + | |||
| + | <font color="green"># Пример кода для k-fold кросс-валидации: | ||
| + | '''# Пример классификатора, cпособного проводить различие между всего лишь двумя | ||
| + | '''# классами, "пятерка" и "не пятерка" из набор данных MNIST</font> | ||
| + | '''import''' numpy '''as''' np | ||
| + | '''from''' sklearn.model_selection '''import''' StratifiedKFold | ||
| + | '''from''' sklearn.datasets '''import''' fetch_openml | ||
| + | '''from''' sklearn.base '''import''' clone | ||
| + | '''from''' sklearn.linear_model '''import''' SGDClassifier | ||
| + | |||
| + | mnist = fetch_openml('mnist_784', version=1) | ||
| + | X, y = mnist["data"], mnist["target"] | ||
| + | y = y.astype(np.uint8) | ||
| + | X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] | ||
| + | y_train_5 = (y_train == 5) <font color="green"> # True для всех пятерок, False для всех остальных цифр. Задача опознать пятерки</font> | ||
| + | y_test_5 = (y_test == 5) | ||
| + | sgd_clf = SGDClassifier(random_state=42)<font color="green"> # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)</font> | ||
| + | <font color="green"># Разбиваем обучающий набора на 3 блока</font> | ||
| + | # выработку прогнозов и их оценку осуществляем на каждом блоке с использованием модели, обученной на остальных блоках</font> | ||
| + | skfolds = StratifiedKFold(n_splits=3, random_state=42) | ||
| + | for train_index, test_index in skfolds.split(X_train, y_train_5): | ||
| + | clone_clf = clone(sgd_clf) | ||
| + | X_train_folds = X_train[train_index] | ||
| + | y_train_folds = y_train_5[train_index] | ||
| + | X_test_fold = X_train[test_index] | ||
| + | y_test_fold = y_train_5[test_index] | ||
| + | clone_clf.fit(X_train_folds, y_train_folds) | ||
| + | y_pred = clone_clf.predict(X_test_fold) | ||
| + | n_correct = sum(y_pred == y_test_fold) | ||
| + | print(n_correct / len(y_pred)) | ||
| + | <font color="green"># print 0.95035 | ||
| + | # 0.96035 | ||
| + | # 0.9604</font> | ||
| + | |||
| + | === t×k-fold кросс-валидация === | ||
| + | # Процедура выполняется <tex>t</tex> раз: | ||
| + | ## Обучающая выборка случайным образом разбивается на <tex>k</tex> непересекающихся одинаковых по объему частей; | ||
| + | ## Производится <tex> k </tex> итераций. На каждой итерации происходит следующее: | ||
| + | ### Модель обучается на <tex> k - 1 </tex> части обучающей выборки; | ||
| + | ### Модель тестируется на части обучающей выборки, которая не участвовала в обучении. | ||
| + | |||
| + | |||
| + | <tex>T^l = F_{(1,1)} \cup \dots \cup F_{(k,1)} = \dots = F_{(1,t)} \cup \dots \cup F_{(k,t)}, |F_{(i,j)}| \approx \frac{l}{k} </tex>, | ||
| + | |||
| + | <tex> CV_{t \times k} = \frac{1}{tk} \sum_{j=1}^t \sum_{i=1}^{k} Q(\mu(T^l \setminus F_{(i,j)}),F_{(i,j)}) \to min </tex>. | ||
| + | |||
| + | === Кросс-валидация по отдельным объектам (Leave-One-Out) === | ||
| + | Выборка разбивается на <tex>l-1</tex> и 1 объект <tex>l</tex> раз. | ||
| + | |||
| + | [[Файл:LeaveOneOut.png|500px]] | ||
| + | |||
| + | <tex>LOO = \frac{1}{l} \sum_{i=1}^{l} Q(\mu(T^l \setminus p_i),p_i) \to min </tex>, где <tex>p_i = (x_i, y_i)</tex>. | ||
| + | |||
| + | Преимущества LOO в том, что каждый объект ровно один раз участвует в контроле, а длина обучающих подвыборок лишь на единицу меньше длины полной выборки. | ||
| + | |||
| + | Недостатком LOO является большая ресурсоёмкость, так как обучаться приходится <tex>L</tex> раз. Некоторые методы обучения позволяют достаточно быстро перенастраивать внутренние параметры алгоритма при замене одного обучающего объекта другим. В этих случаях вычисление LOO удаётся заметно ускорить. | ||
| + | |||
| + | === Случайные разбиения (Random subsampling) === | ||
| + | Выборка разбивается в случайной пропорции. Процедура повторяется несколько раз. | ||
| + | |||
| + | [[Файл:CompleteCrossValidation.png|500px]] | ||
| − | + | === Критерий целостности модели (Model consistency criterion) === | |
| − | + | Не переобученый алгоритм должен показывать одинаковую эффективность на каждой части. | |
| + | |||
| + | [[Файл:ModelConsistencyCriterion.png|500px]] | ||
| + | |||
| + | <tex> D_1 = (\mu, T^{l-t}) = \frac{1}{l} \sum_{i=1}^l (\mu(T^t)(x_i)-\mu(T^{l-t})(x_i)) </tex>, | ||
| − | + | Метод может быть обобщен как аналог <tex> CV_{t \times 2} </tex>. | |
== См. также == | == См. также == | ||
| − | * [[Общие понятия]] | + | * [[Общие понятия]] |
* [[Модель алгоритма и ее выбор]] | * [[Модель алгоритма и ее выбор]] | ||
| − | * [[Мета-обучение]] | + | * [[Мета-обучение]] |
== Примечания == | == Примечания == | ||
# [https://en.wikipedia.org/wiki/Cross-validation_(statistics) Кросс-валидация] | # [https://en.wikipedia.org/wiki/Cross-validation_(statistics) Кросс-валидация] | ||
| − | + | ||
| − | |||
| − | |||
== Источники информации == | == Источники информации == | ||
# [http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D0%BA%D0%BE%D0%BB%D1%8C%D0%B7%D1%8F%D1%89%D0%B8%D0%B9_%D0%BA%D0%BE%D0%BD%D1%82%D1%80%D0%BE%D0%BB%D1%8C Скользящий контроль] - статья на MachineLearning.ru | # [http://www.machinelearning.ru/wiki/index.php?title=%D0%A1%D0%BA%D0%BE%D0%BB%D1%8C%D0%B7%D1%8F%D1%89%D0%B8%D0%B9_%D0%BA%D0%BE%D0%BD%D1%82%D1%80%D0%BE%D0%BB%D1%8C Скользящий контроль] - статья на MachineLearning.ru | ||
| − | # [ | + | # [https://drive.google.com/open?id=1p9CTAa1_gJpj94RXBEcQ09aVOa-KTlrd Model assessment and selection] |
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Автоматическое машинное обучение]] | [[Категория: Автоматическое машинное обучение]] | ||
Текущая версия на 19:32, 4 сентября 2022
Кросс-валидация или скользящий контроль — процедура эмпирического оценивания обобщающей способности алгоритмов. С помощью кросс-валидации эмулируется наличие тестовой выборки, которая не участвует в обучении, но для которой известны правильные ответы.
Содержание
- 1 Определения и обозначения
- 2 Разновидности кросс-валидации
- 2.1 Валидация на отложенных данных (Hold-Out Validation)
- 2.2 Полная кросс-валидация (Complete cross-validation)
- 2.3 k-fold кросс-валидация
- 2.4 t×k-fold кросс-валидация
- 2.5 Кросс-валидация по отдельным объектам (Leave-One-Out)
- 2.6 Случайные разбиения (Random subsampling)
- 2.7 Критерий целостности модели (Model consistency criterion)
- 3 См. также
- 4 Примечания
- 5 Источники информации
Определения и обозначения
Пусть — множество признаков, описывающих объекты, а — конечное множество меток.
— обучающая выборка,
— мера качества,
— модель,
— алгоритм обучения.
Разновидности кросс-валидации
Валидация на отложенных данных (Hold-Out Validation)
Обучающая выборка один раз случайным образом разбивается на две части
После чего решается задача оптимизации:
,
Метод Hold-out применяется в случаях больших датасетов, т.к. требует меньше вычислительных мощностей по сравнению с другими методами кросс-валидации. Недостатком метода является то, что оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения.
Полная кросс-валидация (Complete cross-validation)
- Выбирается значение ;
- Выборка разбивается всеми возможными способами на две части .
,
Здесь число разбиений становится слишком большим даже при сравнительно малых значениях t, что затрудняет практическое применение данного метода.
k-fold кросс-валидация
- Обучающая выборка разбивается на непересекающихся одинаковых по объему частей;
- Производится итераций. На каждой итерации происходит следующее:
- Модель обучается на части обучающей выборки;
- Модель тестируется на части обучающей выборки, которая не участвовала в обучении.
Каждая из частей единожды используется для тестирования. Как правило, (5 в случае малого размера выборки).
.
# Пример кода для k-fold кросс-валидации:
# Пример классификатора, cпособного проводить различие между всего лишь двумя
# классами, "пятерка" и "не пятерка" из набор данных MNIST
import numpy as np
from sklearn.model_selection import StratifiedKFold
from sklearn.datasets import fetch_openml
from sklearn.base import clone
from sklearn.linear_model import SGDClassifier
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для всех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD)
# Разбиваем обучающий набора на 3 блока
# выработку прогнозов и их оценку осуществляем на каждом блоке с использованием модели, обученной на остальных блоках</font>
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = y_train_5[train_index]
X_test_fold = X_train[test_index]
y_test_fold = y_train_5[test_index]
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
# print 0.95035
# 0.96035
# 0.9604
t×k-fold кросс-валидация
- Процедура выполняется раз:
- Обучающая выборка случайным образом разбивается на непересекающихся одинаковых по объему частей;
- Производится итераций. На каждой итерации происходит следующее:
- Модель обучается на части обучающей выборки;
- Модель тестируется на части обучающей выборки, которая не участвовала в обучении.
,
.
Кросс-валидация по отдельным объектам (Leave-One-Out)
Выборка разбивается на и 1 объект раз.
, где .
Преимущества LOO в том, что каждый объект ровно один раз участвует в контроле, а длина обучающих подвыборок лишь на единицу меньше длины полной выборки.
Недостатком LOO является большая ресурсоёмкость, так как обучаться приходится раз. Некоторые методы обучения позволяют достаточно быстро перенастраивать внутренние параметры алгоритма при замене одного обучающего объекта другим. В этих случаях вычисление LOO удаётся заметно ускорить.
Случайные разбиения (Random subsampling)
Выборка разбивается в случайной пропорции. Процедура повторяется несколько раз.
Критерий целостности модели (Model consistency criterion)
Не переобученый алгоритм должен показывать одинаковую эффективность на каждой части.
,
Метод может быть обобщен как аналог .
См. также
Примечания
Источники информации
- Скользящий контроль - статья на MachineLearning.ru
- Model assessment and selection