Метрический классификатор и метод ближайших соседей — различия между версиями
Evaleria (обсуждение | вклад) м (→Метод парзеновского окна) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 11 промежуточных версий 9 участников) | |||
| Строка 7: | Строка 7: | ||
'''Метод <tex>k</tex> ближайших соседей''' (англ. kNN {{---}} <tex>k</tex> Nearest Neighbours) {{---}} Для повышения надёжности классификации объект относится к тому классу, которому принадлежит большинство из его соседей {{---}} <tex>k</tex> ближайших к нему объектов обучающей выборки <tex>x_i</tex>. В задачах с двумя классами число соседей берут нечётным, чтобы не возникало ситуаций неоднозначности, когда одинаковое число соседей принадлежат разным классам. | '''Метод <tex>k</tex> ближайших соседей''' (англ. kNN {{---}} <tex>k</tex> Nearest Neighbours) {{---}} Для повышения надёжности классификации объект относится к тому классу, которому принадлежит большинство из его соседей {{---}} <tex>k</tex> ближайших к нему объектов обучающей выборки <tex>x_i</tex>. В задачах с двумя классами число соседей берут нечётным, чтобы не возникало ситуаций неоднозначности, когда одинаковое число соседей принадлежат разным классам. | ||
| − | '''Метод взвешенных ближайших соседей''' {{---}} в задачах с числом классов 3 и более нечётность уже не помогает | + | '''Метод взвешенных ближайших соседей''' {{---}} в задачах с числом классов 3 и более нечётность уже не помогает и ситуации неоднозначности всё равно могут возникать. Тогда <tex>i</tex>-му соседу приписывается вес <tex>w_i</tex>, как правило, убывающий с ростом ранга соседа <tex>i</tex>. Объект относится к тому классу, который набирает больший суммарный вес среди <tex>k</tex> ближайших соседей. |
== Описание алгоритма == | == Описание алгоритма == | ||
| − | Пусть задана обучающая выборка пар | + | Пусть задана обучающая выборка пар "объект-ответ" <tex>X^m = \{(x_1,y_1),\dots,(x_m,y_m)\}.</tex> |
Пусть на множестве объектов задана функция расстояния <tex>\rho(x,x')</tex>. Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта <tex>x, x'</tex>. | Пусть на множестве объектов задана функция расстояния <tex>\rho(x,x')</tex>. Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта <tex>x, x'</tex>. | ||
| Строка 20: | Строка 20: | ||
<tex>a(u) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] w(i,u)</tex>, | <tex>a(u) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] w(i,u)</tex>, | ||
| − | где <tex>w(i,u)</tex> {{---}} заданная весовая функция, которая оценивает степень важности <tex>i</tex>-го соседа для классификации объекта <tex>u</tex>. Естественно полагать, что эта функция | + | где <tex>w(i,u)</tex> {{---}} заданная весовая функция, которая оценивает степень важности <tex>i</tex>-го соседа для классификации объекта <tex>u</tex>. Естественно полагать, что эта функция не отрицательна и не возрастает по <tex>i</tex> (поскольку чем дальше объект, тем меньший вклад он должен вносить в пользу своего класса). |
По-разному задавая весовую функцию, можно получать различные варианты метода ближайших соседей. | По-разному задавая весовую функцию, можно получать различные варианты метода ближайших соседей. | ||
| Строка 29: | Строка 29: | ||
<tex>w(i,u) = [i\leq k] q^i</tex> {{---}} метод <tex>k</tex> экспоненциально взвешенных ближайших соседей, где предполагается константа <tex>q < 1</tex>; | <tex>w(i,u) = [i\leq k] q^i</tex> {{---}} метод <tex>k</tex> экспоненциально взвешенных ближайших соседей, где предполагается константа <tex>q < 1</tex>; | ||
| + | |||
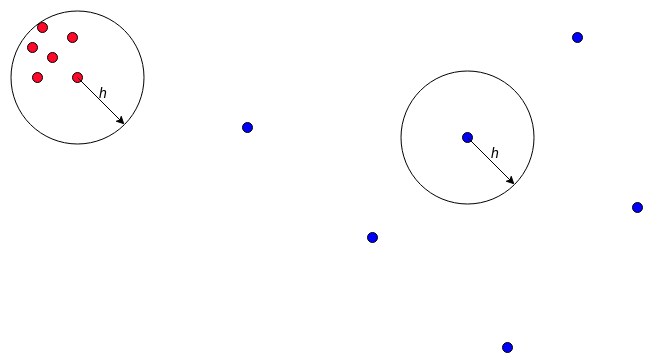
| + | [[Файл:SimpleKnnExample.png|frame|none|super|upright=1|Пример классификации, методом 5 ближайших соседей]] | ||
== Использование ядер сглаживания == | == Использование ядер сглаживания == | ||
| − | При использовании линейной функции в качестве <tex>w(i, u)</tex> возможно совпадение суммарного веса для нескольких классов. Это приводит к неоднозначности ответа при классификации. Чтобы такого не происходило, используют функцию [[Ядра]]<sup>[на | + | При использовании линейной функции в качестве <tex>w(i, u)</tex> возможно совпадение суммарного веса для нескольких классов. Это приводит к неоднозначности ответа при классификации. Чтобы такого не происходило, используют функцию [[Ядра]]<sup>[на 28.01.18 не создан]</sup>. |
Будем обозначать функцию ядра <tex>K(r)</tex>. | Будем обозначать функцию ядра <tex>K(r)</tex>. | ||
| Строка 37: | Строка 39: | ||
=== Примеры ядер === | === Примеры ядер === | ||
| − | Triangular: <tex>{\displaystyle K(r)=(1-|r|)}</tex> | + | Triangular: <tex>{\displaystyle K(r)=(1-|r|)}</tex>, |
| − | Parabolic: <tex>{\displaystyle K(r)={\frac {3}{4}}(1-r^{2})}</tex> | + | Parabolic: <tex>{\displaystyle K(r)={\frac {3}{4}}(1-r^{2})}</tex>, |
| − | Tricube: <tex>{\displaystyle K(r)={\frac {70}{81}}(1-{\left|r\right|}^{3})^{3}}</tex> | + | Tricube: <tex>{\displaystyle K(r)={\frac {70}{81}}(1-{\left|r\right|}^{3})^{3}}</tex>. |
=== Метод парзеновского окна === | === Метод парзеновского окна === | ||
| Строка 53: | Строка 55: | ||
Сравним два этих метода. Сперва запишем классификаторы, полученные при использовании этих методов, в явном виде: | Сравним два этих метода. Сперва запишем классификаторы, полученные при использовании этих методов, в явном виде: | ||
| − | Фиксированной ширины: <tex>a_h = a(u, X^m, \boldsymbol{h}, K) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] K\biggl(\frac{\rho(u,x_{i; u})}{h}\biggr)</tex> | + | Фиксированной ширины: <tex>a_h = a(u, X^m, \boldsymbol{h}, K) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] K\biggl(\frac{\rho(u,x_{i; u})}{h}\biggr)</tex>, |
| − | Переменной ширины: <tex>a_k = a(u, X^m, \boldsymbol{k}, K) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] K\biggl(\frac{\rho(u,x_{i; u})}{\rho(u,x_{k+1; u})}\biggr)</tex> | + | Переменной ширины: <tex>a_k = a(u, X^m, \boldsymbol{k}, K) = \mathrm{arg}\max_{y\in Y} \sum_{i=1}^m \bigl[ y_{i; u}=y \bigr] K\biggl(\frac{\rho(u,x_{i; u})}{\rho(u,x_{k+1; u})}\biggr)</tex>. |
<tex>a_h</tex> не будет учитывать соседей на расстояние больше чем <tex>h</tex>, а всех остальных учтет в соответствии с функций ядра <tex>K</tex>. | <tex>a_h</tex> не будет учитывать соседей на расстояние больше чем <tex>h</tex>, а всех остальных учтет в соответствии с функций ядра <tex>K</tex>. | ||
| Строка 62: | Строка 64: | ||
Часто используют окно переменной ширины т.е. классификатор <tex>a_k</tex>, по следующим причинам: | Часто используют окно переменной ширины т.е. классификатор <tex>a_k</tex>, по следующим причинам: | ||
| − | + | # Удобнее оптимизировать целочисленный параметр <tex>k</tex>, чем вещественный параметр <tex>h</tex> по некоторой сетке; | |
| − | + | # Существует большое количество задач, где точки разбросаны неравномерно. В них могут существовать области, где достаточно брать небольшую <tex>h</tex> и области, где в окно ширины <tex>h</tex> попадает только одна точка. Тогда для классификатора <tex>a_h</tex> будут существовать области в которых не будет ни одного объекта (кроме того, который нужно классифицировать). Для таких областей не понятно как классифицировать объекты. | |
[[Файл:KnnExample.png|frame|none|super|upright=1|Пример классификации, методом с постоянной шириной окна, и неравномерным разбросом точек]] | [[Файл:KnnExample.png|frame|none|super|upright=1|Пример классификации, методом с постоянной шириной окна, и неравномерным разбросом точек]] | ||
== Использование различных метрик расстояния == | == Использование различных метрик расстояния == | ||
| − | Очень редко | + | Очень редко известна хорошая функция расстояния <tex>\rho(x,x')</tex>. В качестве нее обычно использую следующие функции: |
=== Примеры метрик === | === Примеры метрик === | ||
Пусть <tex>x</tex>, <tex>y</tex> {{---}} объекты, а <tex>(x_1, x_2,..., x_n)</tex>, <tex>(y_1, y_2,..., y_n)</tex> их признаковые описания. | Пусть <tex>x</tex>, <tex>y</tex> {{---}} объекты, а <tex>(x_1, x_2,..., x_n)</tex>, <tex>(y_1, y_2,..., y_n)</tex> их признаковые описания. | ||
| − | Евклидова метрика: <tex>\rho(x,y) = \sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}</tex> | + | Евклидова метрика: <tex>\rho(x,y) = \sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}</tex>, |
| − | Расстояние Чебышёва: <tex>\rho(x,y)=\max _{i=1,\dots ,n}|x_{i}-y_{i}|</tex> | + | Расстояние Чебышёва: <tex>\rho(x,y)=\max _{i=1,\dots ,n}|x_{i}-y_{i}|</tex>, |
| − | Манхэттенское Расстояние: <tex>\rho(x,y)=\sum _{i=1}^{n}|x_{i}-y_{i}|</tex> | + | Манхэттенское Расстояние: <tex>\rho(x,y)=\sum _{i=1}^{n}|x_{i}-y_{i}|</tex>. |
| − | При их использовании важно нормировать значения признаков, иначе один признак с максимальным значением может стать | + | При их использовании важно нормировать значения признаков, иначе один признак с максимальным значением может стать преобладающим, а признаки с маленькими значениями не будут учитываться при классификации. Чтобы отсеять лишние признаки (т.е. не влияющие на класс объекта) можно использовать [http://neerc.ifmo.ru/wiki/index.php?title=%D0%A3%D0%BC%D0%B5%D0%BD%D1%8C%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%D1%80%D0%B0%D0%B7%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D0%B8 feature selection]. |
== Пример использования (через scikit-learn) == | == Пример использования (через scikit-learn) == | ||
Рассмотрим использование алгоритма <tex>kNN</tex> на примере [https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29 реального набора данных]. | Рассмотрим использование алгоритма <tex>kNN</tex> на примере [https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29 реального набора данных]. | ||
| − | Предположим, что мы загрузили <tex>wdbc.data</tex> и сохранили как <tex>tr.csv</tex> с заголовком - описанием признаков. | + | Предположим, что мы загрузили <tex>wdbc.data</tex> и сохранили как <tex>tr.csv</tex> с заголовком {{---}} описанием признаков. |
* Загружаем данные | * Загружаем данные | ||
| Строка 116: | Строка 118: | ||
| − | Теперь <tex>X</tex>, <tex>y</tex> - нормированные значения признаков и соответствующие им классы. | + | Теперь <tex>X</tex>, <tex>y</tex> {{---}} нормированные значения признаков и соответствующие им классы. |
| − | * Делим данные на тренировочное и тестовое множество | + | * Делим данные на тренировочное и тестовое множество: |
'''from''' sklearn.model_selection '''import''' train_test_split | '''from''' sklearn.model_selection '''import''' train_test_split | ||
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1234) | X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1234) | ||
| − | * Создаем классификатор | + | * Создаем классификатор: |
'''from''' sklearn.neighbors '''import''' KNeighborsClassifier | '''from''' sklearn.neighbors '''import''' KNeighborsClassifier | ||
| Строка 136: | Строка 138: | ||
) | ) | ||
| − | * Обучаемся | + | * Обучаемся: |
best_model.fit(X_train, y_train) | best_model.fit(X_train, y_train) | ||
| − | * Используем скользящий контроль для поиска лучших параметров (англ. cross validation) | + | * Используем скользящий контроль для поиска лучших параметров (англ. cross validation): |
'''from''' sklearn.model_selection '''import''' GridSearchCV | '''from''' sklearn.model_selection '''import''' GridSearchCV | ||
| Строка 153: | Строка 155: | ||
best_params = clf.best_params_ | best_params = clf.best_params_ | ||
| − | * Оценка классификатора | + | * Оценка классификатора: |
'''from''' sklearn '''import''' metrics | '''from''' sklearn '''import''' metrics | ||
| Строка 160: | Строка 162: | ||
predicted = best_model.predict(X_test) | predicted = best_model.predict(X_test) | ||
| − | * Выводим результат | + | * Выводим результат: |
print('Used params:', best_params) | print('Used params:', best_params) | ||
print('Evaluation:\n', metrics.classification_report(y_test, predicted)) | print('Evaluation:\n', metrics.classification_report(y_test, predicted)) | ||
| Строка 173: | Строка 175: | ||
weighted avg 0.94 0.93 0.93 114 | weighted avg 0.94 0.93 0.93 114 | ||
| − | ==Пример | + | ==Пример на языке Scala== |
SBT зависимость: | SBT зависимость: | ||
libraryDependencies '''+=''' "com.github.haifengl" '''%%''' "smile-scala" '''%''' "1.5.2" | libraryDependencies '''+=''' "com.github.haifengl" '''%%''' "smile-scala" '''%''' "1.5.2" | ||
| Строка 190: | Строка 192: | ||
'''val '''f1Score = '''new '''FMeasure().measure(predictions, y) | '''val '''f1Score = '''new '''FMeasure().measure(predictions, y) | ||
plot(x, y, KNN) | plot(x, y, KNN) | ||
| + | |||
| + | ==Пример на языке Java== | ||
| + | Пример классификации датасета с применением <code>weka.classifiers.lazy.IBk</code><ref>[http://weka.sourceforge.net/doc.stable-3-8/weka/classifiers/lazy/IBk.html/ Weka, KNN]</ref> | ||
| + | |||
| + | <code>Maven</code> зависимость: | ||
| + | <dependency> | ||
| + | <groupId>nz.ac.waikato.cms.weka</groupId> | ||
| + | <artifactId>weka-stable</artifactId> | ||
| + | <version>3.8.0</version> | ||
| + | </dependency> | ||
| + | |||
| + | '''import''' weka.classifiers.Evaluation; | ||
| + | '''import''' weka.classifiers.lazy.IBk; | ||
| + | '''import''' weka.core.converters.ConverterUtils; | ||
| + | |||
| + | <font color="green">// read dataset and build knn-classifier</font> | ||
| + | '''var''' source = new ConverterUtils.DataSource("iris.csv"); | ||
| + | '''var''' dataset = source.getDataSet(); | ||
| + | '''var''' ibk = new IBk(); | ||
| + | ibk.buildClassifier(dataset); | ||
| + | <font color="green">// test the model</font> | ||
| + | '''var''' eTest = new Evaluation(dataset); | ||
| + | eTest.evaluateModel(ibk, dataset); | ||
| + | <font color="green">// print results summary</font> | ||
| + | '''var''' strSummary = eTest.toSummaryString(); | ||
| + | System.out.println(strSummary); | ||
== См. также == | == См. также == | ||
| − | * [[Обзор библиотек для машинного обучения на Python]] | + | * [[Обзор библиотек для машинного обучения на Python]] |
| − | * [[Общие понятия]] | + | * [[Общие понятия]] |
* [[Уменьшение размерности]] | * [[Уменьшение размерности]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
== Источники информации == | == Источники информации == | ||
| − | + | * [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%84%D0%B8%D0%BA%D0%B0%D1%82%D0%BE%D1%80 machinelearning.ru {{---}} Метрический классификатор] | |
| − | + | * [http://www.machinelearning.ru/wiki/index.php?title=KNN machinelearning.ru {{---}} Метод ближайших соседей (kNN)] | |
| − | + | * [https://www.youtube.com/watch?v=l1xGQMowWA4&t=0s&list=PLJOzdkh8T5kp99tGTEFjH_b9zqEQiiBtC&index=3 Лекция "Метрические методы классификации" К.В. Воронцов, курс "Машинное обучение" 2014] | |
| − | + | * [https://en.wikipedia.org/wiki/Kernel_(statistics) Wikipedia {{---}} Kernel (statistics)] | |
| − | + | * [https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html Документация по scikit-learn] | |
| − | + | * [https://www.kaggle.com/jeffbrown/knn-classifier/data Пример по работе с датасетом с kaggle] | |
| + | |||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Метрический классификатор]] | ||
Текущая версия на 19:26, 4 сентября 2022
Метрический классификатор (англ. similarity-based classifier) — алгоритм классификации, основанный на вычислении оценок сходства между объектами.
Для формализации понятия сходства вводится функция расстояния между объектами . Как правило, не требуется, чтобы были выполнены все три аксиомы метрики — неравенство треугольника может нарушаться.
Метод ближайших соседей — простейший метрический классификатор, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Метод ближайших соседей (англ. kNN — Nearest Neighbours) — Для повышения надёжности классификации объект относится к тому классу, которому принадлежит большинство из его соседей — ближайших к нему объектов обучающей выборки . В задачах с двумя классами число соседей берут нечётным, чтобы не возникало ситуаций неоднозначности, когда одинаковое число соседей принадлежат разным классам.
Метод взвешенных ближайших соседей — в задачах с числом классов 3 и более нечётность уже не помогает и ситуации неоднозначности всё равно могут возникать. Тогда -му соседу приписывается вес , как правило, убывающий с ростом ранга соседа . Объект относится к тому классу, который набирает больший суммарный вес среди ближайших соседей.
Содержание
Описание алгоритма
Пусть задана обучающая выборка пар "объект-ответ"
Пусть на множестве объектов задана функция расстояния . Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта .
Для произвольного объекта расположим объекты обучающей выборки в порядке возрастания расстояний до :
, где через обозначается тот объект обучающей выборки, который является -м соседом объекта . Аналогичное обозначение введём и для ответа на -м соседе: . Таким образом, произвольный объект порождает свою перенумерацию выборки. В наиболее общем виде алгоритм ближайших соседей есть: ,
где — заданная весовая функция, которая оценивает степень важности -го соседа для классификации объекта . Естественно полагать, что эта функция не отрицательна и не возрастает по (поскольку чем дальше объект, тем меньший вклад он должен вносить в пользу своего класса).
По-разному задавая весовую функцию, можно получать различные варианты метода ближайших соседей.
— простейший метод ближайшего соседа;
— метод ближайших соседей;
— метод экспоненциально взвешенных ближайших соседей, где предполагается константа ;
Использование ядер сглаживания
При использовании линейной функции в качестве возможно совпадение суммарного веса для нескольких классов. Это приводит к неоднозначности ответа при классификации. Чтобы такого не происходило, используют функцию Ядра[на 28.01.18 не создан].
Будем обозначать функцию ядра .
Примеры ядер
Triangular: ,
Parabolic: ,
Tricube: .
Метод парзеновского окна
Алгоритм ближайших соседей можно обобщить с помощью функции ядра. Рассмотрим два способа, которыми это можно сделать.
— метод парзеновского окна фиксированной ширины ;
— метод парзеновского окна переменной ширины;
Сравним два этих метода. Сперва запишем классификаторы, полученные при использовании этих методов, в явном виде:
Фиксированной ширины: ,
Переменной ширины: .
не будет учитывать соседей на расстояние больше чем , а всех остальных учтет в соответствии с функций ядра . является аналогом метода ближайших соседей (т.к. для всех -ых соседей функция вернет 0), но при этом чем ближе -ый сосед, тем больший вклад в сторону своего класса он даст.
Часто используют окно переменной ширины т.е. классификатор , по следующим причинам:
- Удобнее оптимизировать целочисленный параметр , чем вещественный параметр по некоторой сетке;
- Существует большое количество задач, где точки разбросаны неравномерно. В них могут существовать области, где достаточно брать небольшую и области, где в окно ширины попадает только одна точка. Тогда для классификатора будут существовать области в которых не будет ни одного объекта (кроме того, который нужно классифицировать). Для таких областей не понятно как классифицировать объекты.
Использование различных метрик расстояния
Очень редко известна хорошая функция расстояния . В качестве нее обычно использую следующие функции:
Примеры метрик
Пусть , — объекты, а , их признаковые описания.
Евклидова метрика: ,
Расстояние Чебышёва: ,
Манхэттенское Расстояние: .
При их использовании важно нормировать значения признаков, иначе один признак с максимальным значением может стать преобладающим, а признаки с маленькими значениями не будут учитываться при классификации. Чтобы отсеять лишние признаки (т.е. не влияющие на класс объекта) можно использовать feature selection.
Пример использования (через scikit-learn)
Рассмотрим использование алгоритма на примере реального набора данных. Предположим, что мы загрузили и сохранили как с заголовком — описанием признаков.
- Загружаем данные
import pandas as pd from sklearn.preprocessing import StandardScaler
def load_data(data_path):
ds = pd.read_csv(data_path, names=["id", "diagnosis", "radius_mean", "texture_mean", "perimeter_mean", "area_mean",
"smoothness_mean", "compactness_mean", "concavity_mean", "concave points_mean",
"symmetry_mean", "fractal_dimension_mean", "radius_se", "texture_se",
"perimeter_se", "area_se", "smoothness_se", "compactness_se", "concavity_se",
"concave points_se", "symmetry_se", "fractal_dimension_se", "radius_worst",
"texture_worst", "perimeter_worst", "area_worst", "smoothness_worst",
"compactness_worst", "concavity_worst", "concave points_worst", "symmetry_worst",
"fractal_dimension_worst"])
y = ds['diagnosis']
X = ds.drop('diagnosis', axis=1)
X = X.drop('id', axis=1)
i = len(X.columns)
X = X.drop(X.columns[i - 1], axis=1)
y.replace(('M', 'B'), (1, 0), inplace=True)
sc = StandardScaler()
sc.fit(X)
X_ans = sc.transform(X)
return X_ans, y
X, y = load_data("tr.csv")
Теперь , — нормированные значения признаков и соответствующие им классы.
- Делим данные на тренировочное и тестовое множество:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1234)
- Создаем классификатор:
from sklearn.neighbors import KNeighborsClassifier
best_model = KNeighborsClassifier( n_neighbors=10, weights=’distance’, algorithm=’auto’, leaf_size=30, metric=’euclidean’, metric_params=None, n_jobs=4 )
- Обучаемся:
best_model.fit(X_train, y_train)
- Используем скользящий контроль для поиска лучших параметров (англ. cross validation):
from sklearn.model_selection import GridSearchCV
model_params = best_model.get_params()
tuned_params = {}
for k, v in model_params.items():
tuned_params[k] = [v]
tuned_params['n_neighbors'] = range(1, 30)
clf = GridSearchCV(KNeighborsClassifier(), tuned_params, cv=10, n_jobs=-1)
clf.fit(X_train, y_train)
best_params = clf.best_params_
- Оценка классификатора:
from sklearn import metrics
best_model = KNeighborsClassifier(**best_params) best_model.fit(X_train, y_train) predicted = best_model.predict(X_test)
- Выводим результат:
print('Used params:', best_params)
print('Evaluation:\n', metrics.classification_report(y_test, predicted))
> Used params: {'metric_params': None, 'metric': 'euclidean', 'weights': 'distance', 'n_neighbors': 9, 'leaf_size': 30, 'n_jobs': 4, 'p': 2, 'algorithm': 'auto'}
Evaluation:
precision recall f1-score support
0 0.90 1.00 0.95 69
1 1.00 0.82 0.90 45
micro avg 0.93 0.93 0.93 114
macro avg 0.95 0.91 0.92 114
weighted avg 0.94 0.93 0.93 114
Пример на языке Scala
SBT зависимость:
libraryDependencies += "com.github.haifengl" %% "smile-scala" % "1.5.2"
Пример классификации датасета и вычисления F1 меры[1] используя smile.classification.knn[2]:
import smile.classification._ import smile.data._ import smile.plot._ import smile.read import smile.validation.FMeasure
val toy: AttributeDataset = read.table("iris.csv", delimiter = ",", response = Some((new NumericAttribute("class"), 2)))
val x: Array[Array[Double]] = toy.x()
val y: Array[Int] = toy.y().map(_.toInt)
val KNN: KNN[Array[Double]] = knn(x, y, 3)
val predictions: Array[Int] = x.map(KNN.predict)
val f1Score = new FMeasure().measure(predictions, y)
plot(x, y, KNN)
Пример на языке Java
Пример классификации датасета с применением weka.classifiers.lazy.IBk[3]
Maven зависимость:
<dependency> <groupId>nz.ac.waikato.cms.weka</groupId> <artifactId>weka-stable</artifactId> <version>3.8.0</version> </dependency>
import weka.classifiers.Evaluation; import weka.classifiers.lazy.IBk; import weka.core.converters.ConverterUtils;
// read dataset and build knn-classifier
var source = new ConverterUtils.DataSource("iris.csv");
var dataset = source.getDataSet();
var ibk = new IBk();
ibk.buildClassifier(dataset);
// test the model
var eTest = new Evaluation(dataset);
eTest.evaluateModel(ibk, dataset);
// print results summary
var strSummary = eTest.toSummaryString();
System.out.println(strSummary);