Выброс — различия между версиями
Fest (обсуждение | вклад) (→Пример) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 51 промежуточная версия 10 участников) | |||
| Строка 1: | Строка 1: | ||
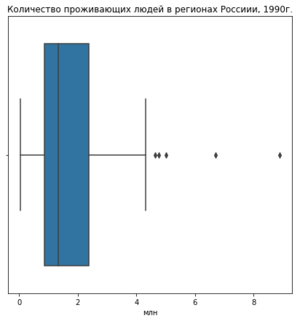
[[Файл:Outlier_boxplot.png|upright=1.0|thumb|Рис 1.График boxplot населения регионов России в 1990 году, где можно заметить 5 выбросов]] | [[Файл:Outlier_boxplot.png|upright=1.0|thumb|Рис 1.График boxplot населения регионов России в 1990 году, где можно заметить 5 выбросов]] | ||
| − | '''Выброс'''(англ. ''outlier'') | + | '''Выброс''' (англ. ''outlier'') {{---}} это экстремальные значения во входных данных, которые находятся далеко за пределами других наблюдений. Например, все предметы на кухне имеют температуру около 22-25 грудусов Цельсия, а {{---}} духовка 220. |
| + | |||
| + | Многие алгоритмы машинного обучения чувствительны к разбросу и распределению значений признаков обрабатываемых объектов. Соответственно, выбросы во входных данных могут исказить и ввести в заблуждение процесс обучения алгоритмов машинного обучения, что приводит к увеличению времени обучения, снижению точности моделей и, в конечном итоге, к снижению результатов. Даже до подготовки предсказательных моделей на основе обучающих данных выбросы могут приводить к ошибочным представлениям и в дальнейшем к ошибочной интерпретации собранных данных. | ||
===Виды выбросов=== | ===Виды выбросов=== | ||
| − | + | На основе размерности изучаемого массива данных выбросы подразделяют на одномерные и многомерные. | |
| − | + | ;Одномерные выбросы | |
| − | + | :Точка является выбросом только по одной из своих координат. | |
| + | ;Многомерные выбросы | ||
| + | :Точка является выбросом сразу по нескольким координатам. | ||
| + | |||
| + | Другой подход классификации выбросов {{---}} по их окружению. | ||
| + | ;Точечные выбросы | ||
| + | :Единичные точки, выбивающиеся из общей картины. Точечные аномалии часто используются в системах контроля транзакций для выявления мошенничества, например, когда с украденной карты совершается крупная покупка. | ||
| + | ;Контекстуальные выбросы | ||
| + | :Для того, чтобы определить, является ли точка выбросом необходим контекст. Например, в Петербурге +15 градусов Цельсия. Зимой такая температура является выбросом, а летом нет. | ||
| + | ;Коллективные выбросы | ||
| + | :Здесь выбросом является не точка, а группа точек. Примером таких выбросов могут служить, например, задержки поставок на фабрике. Одна задержка не является выбросом. Но если их много, значит это может стать проблемой. | ||
===Причины возникновения выбросов=== | ===Причины возникновения выбросов=== | ||
| − | * Сбой работы оборудования | + | * Сбой работы оборудования; |
| − | * Человеческий фактор | + | * Человеческий фактор; |
| − | * Случайность | + | * Случайность; |
| − | * Уникальные явления | + | * Уникальные явления; |
* и др. | * и др. | ||
==Примеры== | ==Примеры== | ||
| Строка 21: | Строка 33: | ||
==Методы обнаружения и борьбы с выбросами== | ==Методы обнаружения и борьбы с выбросами== | ||
===Методы обнаружения выбросов=== | ===Методы обнаружения выбросов=== | ||
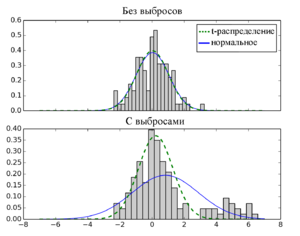
| − | [[Файл:Outlier_normal_distribution.png|upright=1.0|thumb|[http://work.thaslwanter.at/Stats/html/statsDistributions.html Так как t-распределение имеет более длинный хвост, нежели у нормального распределения, поэтому t-распределение менее чувствительно к выбросам.]]] | + | [[Файл:Outlier_normal_distribution.png|upright=1.0|thumb|[http://work.thaslwanter.at/Stats/html/statsDistributions.html Рис 4. Так как t-распределение имеет более длинный хвост, нежели у нормального распределения, поэтому t-распределение менее чувствительно к выбросам.]]] |
# Экстремальный анализ данных(англ. ''extreme value analysis''). При таком анализе не применяются какие-либо специальные статистические методы. Обычно этот метод применим для одномерного случая. Алгоритм использования таков: | # Экстремальный анализ данных(англ. ''extreme value analysis''). При таком анализе не применяются какие-либо специальные статистические методы. Обычно этот метод применим для одномерного случая. Алгоритм использования таков: | ||
| − | #* Визуализировать данные, используя диаграммы и гистограммы для нахождения экстремальных значений | + | #* Визуализировать данные, используя диаграммы и гистограммы для нахождения экстремальных значений; |
| − | #* Задействовать распределение, например Гауссовское, и найти значения, чье стандартное отклонение отличается в 2-3 раза от математического ожидания или в полтора раза от первой либо третьей квартилей | + | #* Задействовать распределение, например Гауссовское, и найти значения, чье стандартное отклонение отличается в 2-3 раза от математического ожидания или в полтора раза от первой либо третьей квартилей; |
| − | #* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели | + | #* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели; |
| − | # | + | # Аппроксимирующий метод (англ. ''proximity method''). Чуть более сложный метод, заключающийся в применении кластеризующих методов; |
| − | #* Использовать метод кластеризации для определения кластеров | + | #* Использовать метод кластеризации для определения кластеров в данных; |
| − | #* Идентифицировать и отметить центроиды каждого кластера | + | #* Идентифицировать и отметить центроиды каждого кластера; |
| − | #* Соотнести кластеры с экземплярами данных, находящимися на фиксированном расстоянии или на процентном удалении от | + | #* Соотнести кластеры с экземплярами данных, находящимися на фиксированном расстоянии или на процентном удалении от центроида соответствующего кластера; |
| − | #* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели | + | #* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели; |
| − | # Проецирующие методы (англ. ''projections methods''). Эти методы довольно быстро и просто определяют выбросы в выборке | + | # Проецирующие методы (англ. ''projections methods''). Эти методы довольно быстро и просто определяют выбросы в выборке; |
| − | #* Использовать один из проецирующих методов, например метод главных компонент (англ. ''principal component analysis'', ''PCA''<ref>[https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 Метод главных компонент]</ref>) или самоорганизующиеся карты Кохонена(англ. ''self-organizing map'', ''SOM''<ref>[https://habr.com/post/338868/ Самоорганизующиеся карты Кохонена]</ref>) или проекцию Саммона(англ. ''Sammon mapping'', ''Sammon projection''<ref>[https://en.wikipedia.org/wiki/Sammon_mapping Проекция Саммона]</ref>), для суммирования обучающих данных в двух измерениях | + | #* Использовать один из проецирующих методов, например, метод главных компонент (англ. ''principal component analysis'', ''PCA''<ref>[https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D1%8B%D1%85_%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%82 Метод главных компонент]</ref>) или самоорганизующиеся карты Кохонена(англ. ''self-organizing map'', ''SOM''<ref>[https://habr.com/post/338868/ Самоорганизующиеся карты Кохонена]</ref>) или проекцию Саммона(англ. ''Sammon mapping'', ''Sammon projection''<ref>[https://en.wikipedia.org/wiki/Sammon_mapping Проекция Саммона]</ref>), для суммирования обучающих данных в двух измерениях; |
| − | #* Визуализировать отображение | + | #* Визуализировать отображение; |
| − | #* Использовать критерий близости от проецируемых значений или от вектора таблицы кодирования (англ. ''codebook vector'') для идентифицирования выбросов | + | #* Использовать критерий близости от проецируемых значений или от вектора таблицы кодирования (англ. ''codebook vector'') для идентифицирования выбросов; |
#* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели. | #* Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели. | ||
===Локально взвешенное сглаживание=== | ===Локально взвешенное сглаживание=== | ||
| − | Локально взвешенное сглаживание(англ. ''LOcally WEighted Scatter plot Smoothing'', ''LOWESS'')<ref>[http://www.aliquote.org/cours/2012_biomed/biblio/Cleveland1979.pdf Локально взвешенное сглаживание]</ref>. Данная методика была предложена Кливлендом(Cleveland) в 1979 году для моделирования и сглаживания двумерных данных <math>X^m={(x_i, y_i)}_{i=1}^m</math>. Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. Локально-линейная модель может быть записана в виде: <math>y_t=\alpha_t+\beta_t x_t + \varepsilon_t</math>. Эта модель может быть расширена на случай локально-квадратичной зависимости и на модель с | + | Локально взвешенное сглаживание (англ. ''LOcally WEighted Scatter plot Smoothing'', ''LOWESS'')<ref>[http://www.aliquote.org/cours/2012_biomed/biblio/Cleveland1979.pdf Локально взвешенное сглаживание]</ref>. Данная методика была предложена Кливлендом (Cleveland) в 1979 году для моделирования и сглаживания двумерных данных <math>X^m={(x_i, y_i)}_{i=1}^m</math>. Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. Локально-линейная модель может быть записана в виде: <math>y_t=\alpha_t+\beta_t x_t + \varepsilon_t</math>. Эта модель может быть расширена на случай локально-квадратичной зависимости и на модель с большим числом независимых переменных. Параметры <math>\alpha_t</math> и <math>\beta_t</math> локально линейной модели оцениваются с помощью локально взвешенной регрессии, которая присваивает объекту тем больший вес, чем более близок он к объекту t. Степень сглаживания определяется параметром сглаживания <math>f</math>, который выбирает пользователь. Параметр <math>f</math> указывает какая доля (англ. ''fraction'') данных используется в процедуре. Если <math>f = 0.5</math>, то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если <math>f = 0.8</math>, то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше, чем они ближе к объекту <math>t</math>. |
====Постановка задачи==== | ====Постановка задачи==== | ||
| − | Пусть задано пространство объектов X и множество возможных ответов <math>Y = \mathbb{R}</math>. Существует неизвестная зависимость <math>y^*\colon X \to Y</math>, значения которой известны только на объектах обучающией выборки <math>X^l = (x_i\ ,\ y_i)^l_{i=1},\ y_i = y^*(x_i)</math>. Требуется построить алгоритм <math>a\colon X\to Y</math>, аппроксимирующий неизвестную зависимость <math>y^*</math>. Предполагается, что на множестве X задана метрика <math>\rho(x,x')</math>. | + | Пусть задано пространство объектов $X$ и множество возможных ответов <math>Y = \mathbb{R}</math>. Существует неизвестная зависимость <math>y^*\colon X \to Y</math>, значения которой известны только на объектах обучающией выборки <math>X^l = (x_i\ ,\ y_i)^l_{i=1},\ y_i = y^*(x_i)</math>. Требуется построить алгоритм <math>a\colon X\to Y</math>, аппроксимирующий неизвестную зависимость <math>y^*</math>. Предполагается, что на множестве $X$ задана метрика <math>\rho(x,x')</math>. |
| − | Также стоит определить следующее. Для вычисления <math>a(x) = \alpha</math> | + | |
| − | <math>Q(\alpha;X^l) = \sum_{i=1}^l \omega_i(x)(\alpha-y_i)^2 \rightarrow \underset{\alpha \in \mathbb{R}}{min}</math>, где <math>\omega_i</math> - это вес i-ого объекта. Веса <math>\omega_i</math> разумно задать так, чтобы они убывали по мере увеличения расстояния <math>\rho(x,x_i)</math>. Для этого можно ввести невозрастающую, гладкую, ограниченную функцию <math>K:[0, \infty) \rightarrow [0, \infty)</math>, называемую ядром, и представить <math>\omega_i</math> в следующем виде : | + | Также стоит определить следующее. Для вычисления <math>a(x) = \alpha</math> для <math>\forall x \in X</math> воспользуемся методом наименьших квадратов: |
| − | <math>\omega_i(x) = K\left(\frac{\rho(x,x_i)}{h} \right )</math>, где h | + | <math>Q(\alpha;X^l) = \sum_{i=1}^l \omega_i(x)(\alpha-y_i)^2 \rightarrow \underset{\alpha \in \mathbb{R}}{min}</math>, где <math>\omega_i</math> {{---}} это вес $i$-ого объекта. |
| − | Приравняв нулю производную <math>\frac{\partial Q}{\partial \alpha} = 0</math> | + | |
| − | <math>a_h(x;X^l) = \frac{\sum_{i=1}^{l} y_i\omega_i(x)}{\sum_{i=1}^{l} \omega_i(x)} = \frac{\sum_{i=1}^{l} y_iK\left(\frac{\rho(x,x_i)}{h} \right )}{\sum_{i=1}^{l} K\left(\frac{\rho(x,x_i)}{h} \right )}</math> | + | Веса <math>\omega_i</math> разумно задать так, чтобы они убывали по мере увеличения расстояния <math>\rho(x,x_i)</math>. Для этого можно ввести невозрастающую, гладкую, ограниченную функцию <math>K:[0, \infty) \rightarrow [0, \infty)</math>, называемую [[Ядра|ядром]]<sup>[на 28.01.19 не создан]</sup>, и представить <math>\omega_i</math> в следующем виде: |
| + | |||
| + | |||
| + | <math>\omega_i(x) = K\left(\frac{\rho(x,x_i)}{h} \right )</math>, где $h$ {{---}} ширина окна. | ||
| + | |||
| + | |||
| + | Приравняв равной нулю производную <math>\frac{\partial Q}{\partial \alpha} = 0</math> и выразив <math>\alpha</math>, получаем ''формулу Надарая-Ватсона''<ref>[http://www.machinelearning.ru/wiki/index.php?title=%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B0_%D0%9D%D0%B0%D0%B4%D0%B0%D1%80%D0%B0%D1%8F-%D0%92%D0%B0%D1%82%D1%81%D0%BE%D0%BD%D0%B0 Формула Надарая-Ватсона]</ref> : | ||
| + | <math>a_h(x;X^l) = \frac{\sum_{i=1}^{l} y_i\omega_i(x)}{\sum_{i=1}^{l} \omega_i(x)} = \frac{\sum_{i=1}^{l} y_iK\left(\frac{\rho(x,x_i)}{h} \right )}{\sum_{i=1}^{l} K\left(\frac{\rho(x,x_i)}{h} \right )}</math>. | ||
====Проблема выбросов в этой задаче==== | ====Проблема выбросов в этой задаче==== | ||
| − | Большие случайные ошибки в значениях <math>y_i</math> сильно искажают оценку Надарая-Ватсона | + | Большие случайные ошибки в значениях <math>y_i</math> сильно искажают оценку Надарая-Ватсона. |
====Идея==== | ====Идея==== | ||
| − | Чем больше величина невязки <math>\varepsilon_i = \left | a_h\left (x_i;X^\ell\backslash\left \{x_i\right \} \right )-y_i\right |</math>, тем меньше должен быть вес i-го объекта <math>\omega_i(x)</math> | + | Чем больше величина невязки <math>\varepsilon_i = \left | a_h\left (x_i;X^\ell\backslash\left \{x_i\right \} \right )-y_i\right |</math>, тем меньше должен быть вес i-го объекта <math>\omega_i(x)</math>. |
====Эвристика==== | ====Эвристика==== | ||
| − | Домножить веса <math>\omega_i(x)</math> на | + | Домножить веса <math>\omega_i(x)</math> на коэффициенты <math>\gamma_i = \widetilde{K}\left ( \varepsilon_i \right )</math>, где <math>\widetilde{K}\left ( \varepsilon \right )</math> — ещё одно ядро, вообще говоря, отличное от <math>K\left ( \rho \right )</math>. |
====Псевдокод==== | ====Псевдокод==== | ||
| − | + | INPUT: <math>X^\ell</math> - training sample; | |
| − | + | OUTPUT: coefficents <math>\gamma_i, i = 1,...,\ell</math>; | |
________________________________________________________ | ________________________________________________________ | ||
| − | 1: | + | 1: initialization: <math>\gamma_i := 1, i = 1,...,\ell</math>; <span style="color:green">//инициализация коэффициентов</span> |
| − | 2: | + | 2: do |
| − | 3: | + | 3: for each object <math>i = 1,...,\ell</math>; |
| − | 4: вычислить оценки скользящего контроля | + | 4: calculate cross-validation estimates: <span style="color:green">//вычислить оценки скользящего контроля</span> |
<math>a_i := a_h(x_i;X^\ell\setminus{x_i}) = \frac{\sum\limits^{\ell}_{j=1,j\ne i} {y_j\gamma_j K \left ( \tfrac{\rho\left (x_i,x_j \right )}{h\left (x_i \right)} \right )}}{\sum\limits^{\ell}_{j=1,j\ne i}{\gamma_j K\left(\tfrac{\rho\left (x_i,x_j \right )}{h\left (x_i\right )}\right )} }</math> | <math>a_i := a_h(x_i;X^\ell\setminus{x_i}) = \frac{\sum\limits^{\ell}_{j=1,j\ne i} {y_j\gamma_j K \left ( \tfrac{\rho\left (x_i,x_j \right )}{h\left (x_i \right)} \right )}}{\sum\limits^{\ell}_{j=1,j\ne i}{\gamma_j K\left(\tfrac{\rho\left (x_i,x_j \right )}{h\left (x_i\right )}\right )} }</math> | ||
| − | 5: | + | 5: for each object <math>i = 1,...,\ell</math>; |
6: <math>\gamma_i := \widetilde{K}\left (\left | a_i-y_i \right | \right );</math> | 6: <math>\gamma_i := \widetilde{K}\left (\left | a_i-y_i \right | \right );</math> | ||
| − | 7: | + | 7: while coefficents <math>\gamma_i</math> not stabilized; <span style="color:green">//пока коэффициенты не стабилизируются</span> |
| − | ====Пример==== | + | |
| − | В этом примере мы попытаемся локально регрессировать и сгладить | + | ====Пример на языке R==== |
| + | В этом примере мы попытаемся локально регрессировать и сгладить среднюю продолжительность безработицы на основе набора экономических данных из пакета $ggplot2$ языка $R$. Мы рассматриваем только первые 80 строк для этого анализа, чтобы легче было наблюдать степень сглаживания на приведенных ниже графиках.<br> | ||
| + | data(economics, package="ggplot2") <span style="color:green"># загрузка данных</span> | ||
| + | economics$index <- 1:nrow(economics) <span style="color:green"># создание индексной переменной</span> | ||
| + | economics <- economics[1:80, ] <span style="color:green"># усечение до 80 строк для более наглядного демонстрирования</span> | ||
| + | loessMod10 <- loess(uempmed ~ index, data=economics, span=0.10) <span style="color:green"># 10% параметр сглаживания span</span> | ||
| + | loessMod25 <- loess(uempmed ~ index, data=economics, span=0.25) <span style="color:green"># 25% параметр сглаживания span</span> | ||
| + | loessMod50 <- loess(uempmed ~ index, data=economics, span=0.50) <span style="color:green"># 50% параметр сглаживания span</span> | ||
| + | |||
| + | <span style="color:green"># получить сглаженный результат</span> | ||
| + | smoothed10 <- predict(loessMod10) | ||
| + | smoothed25 <- predict(loessMod25) | ||
| + | smoothed50 <- predict(loessMod50) | ||
| + | |||
| + | <span style="color:green"># Нарисовать</span> | ||
| + | plot(economics''$''uempmed, x=economics''$''date, type="l", main="Локально взвешенное сглаживание", xlab="Дата", ylab="Длительность безработицы") | ||
| + | lines(smoothed10, x=economics''$''date, col="red") | ||
| + | lines(smoothed25, x=economics''$''date, col="green") | ||
| + | lines(smoothed50, x=economics''$''date, col="blue") | ||
| + | {|align="center" | ||
| + | |-valign="top" | ||
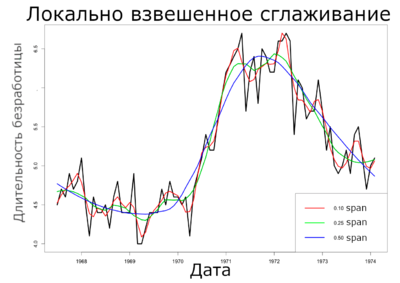
| + | |[[Файл:LOWESS.png|400px|thumb|Рис 5. На приведенном графике показано, что чем больше параметр сглаживания span, тем более сглаженной выглядит восстановленная регрессия]] | ||
| + | |} | ||
===Другие алгоритмы борьбы с выбросами=== | ===Другие алгоритмы борьбы с выбросами=== | ||
В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются ''робастными''. Метод локально взвешенного сглаживания относится к ''робастным'' методам, так как он устойчив к наличию небольшого количества выбросов. | В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются ''робастными''. Метод локально взвешенного сглаживания относится к ''робастным'' методам, так как он устойчив к наличию небольшого количества выбросов. | ||
| − | * Дерево принятия решения (англ. ''decision tree''<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B9 Дерево принятия решения]</ref>). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится к ''робастным'' методам | + | * [[Дерево решений и случайный лес|Дерево принятия решения]] (англ. ''decision tree''<ref>[https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B9 Дерево принятия решения]</ref>). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится к ''робастным'' методам; |
| − | * Робастная регрессия (англ. ''robust regression''<ref>[https://en.wikipedia.org/wiki/Robust_regression Робастная регрессия]</ref>). В | + | * [[Вариации регрессии|Робастная регрессия]] (англ. ''robust regression''<ref>[https://en.wikipedia.org/wiki/Robust_regression Робастная регрессия]</ref>). В отличие от регрессии, использующей, например, метод наименьших квадратов, в этом алгоритме не строится идеализированное предположение, что вектор ошибок <math>\varepsilon</math> распределен согласно нормальному закону. Однако на практике зачастую имеют место отклонения от этого предположения. Тогда можно применить метод наименьших модулей (англ. ''Least Absolute Deviation, LAD ''<ref>[https://en.wikipedia.org/wiki/Least_absolute_deviations Метод наименьших модулей]</ref>) в случае, если распределение ошибок измерений подчиняется распределению Лапласа (англ. Laplace distribution <ref>[https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0 Распределение Лапласа]</ref>). |
==См.также== | ==См.также== | ||
| − | * [[ | + | * [[Общие понятия]] |
* [[Переобучение]] | * [[Переобучение]] | ||
| + | * [[Дерево решений и случайный лес]] | ||
==Примечания== | ==Примечания== | ||
| Строка 84: | Строка 126: | ||
# https://machinelearningmastery.com/how-to-identify-outliers-in-your-data/ | # https://machinelearningmastery.com/how-to-identify-outliers-in-your-data/ | ||
# https://ru.coursera.org/lecture/vvedenie-mashinnoe-obuchenie/obnaruzhieniie-vybrosov-t9PG4 | # https://ru.coursera.org/lecture/vvedenie-mashinnoe-obuchenie/obnaruzhieniie-vybrosov-t9PG4 | ||
| + | # https://www.reg.ru/blog/ishchem-anomalii-s-python-chast-1/ | ||
| + | |||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Статистика]] | [[Категория: Статистика]] | ||
Текущая версия на 19:13, 4 сентября 2022
Выброс (англ. outlier) — это экстремальные значения во входных данных, которые находятся далеко за пределами других наблюдений. Например, все предметы на кухне имеют температуру около 22-25 грудусов Цельсия, а — духовка 220.
Многие алгоритмы машинного обучения чувствительны к разбросу и распределению значений признаков обрабатываемых объектов. Соответственно, выбросы во входных данных могут исказить и ввести в заблуждение процесс обучения алгоритмов машинного обучения, что приводит к увеличению времени обучения, снижению точности моделей и, в конечном итоге, к снижению результатов. Даже до подготовки предсказательных моделей на основе обучающих данных выбросы могут приводить к ошибочным представлениям и в дальнейшем к ошибочной интерпретации собранных данных.
Содержание
Виды выбросов
На основе размерности изучаемого массива данных выбросы подразделяют на одномерные и многомерные.
- Одномерные выбросы
- Точка является выбросом только по одной из своих координат.
- Многомерные выбросы
- Точка является выбросом сразу по нескольким координатам.
Другой подход классификации выбросов — по их окружению.
- Точечные выбросы
- Единичные точки, выбивающиеся из общей картины. Точечные аномалии часто используются в системах контроля транзакций для выявления мошенничества, например, когда с украденной карты совершается крупная покупка.
- Контекстуальные выбросы
- Для того, чтобы определить, является ли точка выбросом необходим контекст. Например, в Петербурге +15 градусов Цельсия. Зимой такая температура является выбросом, а летом нет.
- Коллективные выбросы
- Здесь выбросом является не точка, а группа точек. Примером таких выбросов могут служить, например, задержки поставок на фабрике. Одна задержка не является выбросом. Но если их много, значит это может стать проблемой.
Причины возникновения выбросов
- Сбой работы оборудования;
- Человеческий фактор;
- Случайность;
- Уникальные явления;
- и др.
Примеры
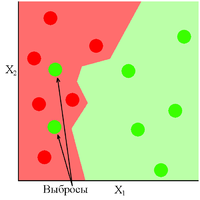
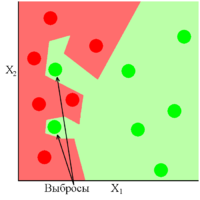
Рис 2 показывает хорошо обученную модель, в которой присутствуют два выброса. Как видно из рисунка данная модель показала себя устойчивой к выбросам, либо же вовремя прекратила своё обучение. Обратная ситуация обстоит с Рис 3, где модель сильно переобучилась из-за присутствующих в ней выбросов.
Методы обнаружения и борьбы с выбросами
Методы обнаружения выбросов
- Экстремальный анализ данных(англ. extreme value analysis). При таком анализе не применяются какие-либо специальные статистические методы. Обычно этот метод применим для одномерного случая. Алгоритм использования таков:
- Визуализировать данные, используя диаграммы и гистограммы для нахождения экстремальных значений;
- Задействовать распределение, например Гауссовское, и найти значения, чье стандартное отклонение отличается в 2-3 раза от математического ожидания или в полтора раза от первой либо третьей квартилей;
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели;
- Аппроксимирующий метод (англ. proximity method). Чуть более сложный метод, заключающийся в применении кластеризующих методов;
- Использовать метод кластеризации для определения кластеров в данных;
- Идентифицировать и отметить центроиды каждого кластера;
- Соотнести кластеры с экземплярами данных, находящимися на фиксированном расстоянии или на процентном удалении от центроида соответствующего кластера;
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели;
- Проецирующие методы (англ. projections methods). Эти методы довольно быстро и просто определяют выбросы в выборке;
- Использовать один из проецирующих методов, например, метод главных компонент (англ. principal component analysis, PCA[1]) или самоорганизующиеся карты Кохонена(англ. self-organizing map, SOM[2]) или проекцию Саммона(англ. Sammon mapping, Sammon projection[3]), для суммирования обучающих данных в двух измерениях;
- Визуализировать отображение;
- Использовать критерий близости от проецируемых значений или от вектора таблицы кодирования (англ. codebook vector) для идентифицирования выбросов;
- Отфильтровать предполагаемые выбросы из обучающей выборки и оценить работу модели.
Локально взвешенное сглаживание
Локально взвешенное сглаживание (англ. LOcally WEighted Scatter plot Smoothing, LOWESS)[4]. Данная методика была предложена Кливлендом (Cleveland) в 1979 году для моделирования и сглаживания двумерных данных . Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. Локально-линейная модель может быть записана в виде: . Эта модель может быть расширена на случай локально-квадратичной зависимости и на модель с большим числом независимых переменных. Параметры и локально линейной модели оцениваются с помощью локально взвешенной регрессии, которая присваивает объекту тем больший вес, чем более близок он к объекту t. Степень сглаживания определяется параметром сглаживания , который выбирает пользователь. Параметр указывает какая доля (англ. fraction) данных используется в процедуре. Если , то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если , то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше, чем они ближе к объекту .
Постановка задачи
Пусть задано пространство объектов $X$ и множество возможных ответов . Существует неизвестная зависимость , значения которой известны только на объектах обучающией выборки . Требуется построить алгоритм , аппроксимирующий неизвестную зависимость . Предполагается, что на множестве $X$ задана метрика .
Также стоит определить следующее. Для вычисления для воспользуемся методом наименьших квадратов: , где — это вес $i$-ого объекта.
Веса разумно задать так, чтобы они убывали по мере увеличения расстояния . Для этого можно ввести невозрастающую, гладкую, ограниченную функцию , называемую ядром[на 28.01.19 не создан], и представить в следующем виде:
, где $h$ — ширина окна.
Приравняв равной нулю производную и выразив , получаем формулу Надарая-Ватсона[5] :
.
Проблема выбросов в этой задаче
Большие случайные ошибки в значениях сильно искажают оценку Надарая-Ватсона.
Идея
Чем больше величина невязки , тем меньше должен быть вес i-го объекта .
Эвристика
Домножить веса на коэффициенты , где — ещё одно ядро, вообще говоря, отличное от .
Псевдокод
INPUT: - training sample; OUTPUT: coefficents ; ________________________________________________________ 1: initialization: ; //инициализация коэффициентов 2: do 3: for each object ; 4: calculate cross-validation estimates: //вычислить оценки скользящего контроля 5: for each object ; 6: 7: while coefficents not stabilized; //пока коэффициенты не стабилизируются
Пример на языке R
В этом примере мы попытаемся локально регрессировать и сгладить среднюю продолжительность безработицы на основе набора экономических данных из пакета $ggplot2$ языка $R$. Мы рассматриваем только первые 80 строк для этого анализа, чтобы легче было наблюдать степень сглаживания на приведенных ниже графиках.
data(economics, package="ggplot2") # загрузка данных economics$index <- 1:nrow(economics) # создание индексной переменной economics <- economics[1:80, ] # усечение до 80 строк для более наглядного демонстрирования loessMod10 <- loess(uempmed ~ index, data=economics, span=0.10) # 10% параметр сглаживания span loessMod25 <- loess(uempmed ~ index, data=economics, span=0.25) # 25% параметр сглаживания span loessMod50 <- loess(uempmed ~ index, data=economics, span=0.50) # 50% параметр сглаживания span
# получить сглаженный результат
smoothed10 <- predict(loessMod10)
smoothed25 <- predict(loessMod25)
smoothed50 <- predict(loessMod50)
# Нарисовать
plot(economics$uempmed, x=economics$date, type="l", main="Локально взвешенное сглаживание", xlab="Дата", ylab="Длительность безработицы")
lines(smoothed10, x=economics$date, col="red")
lines(smoothed25, x=economics$date, col="green")
lines(smoothed50, x=economics$date, col="blue")
Другие алгоритмы борьбы с выбросами
В статистике методы, устойчивые к нарушениям модельных предположений о данных, называются робастными. Метод локально взвешенного сглаживания относится к робастным методам, так как он устойчив к наличию небольшого количества выбросов.
- Дерево принятия решения (англ. decision tree[6]). Это дерево, как и уже описанный алгоритм локально взвешенного сглаживания, относится к робастным методам;
- Робастная регрессия (англ. robust regression[7]). В отличие от регрессии, использующей, например, метод наименьших квадратов, в этом алгоритме не строится идеализированное предположение, что вектор ошибок распределен согласно нормальному закону. Однако на практике зачастую имеют место отклонения от этого предположения. Тогда можно применить метод наименьших модулей (англ. Least Absolute Deviation, LAD [8]) в случае, если распределение ошибок измерений подчиняется распределению Лапласа (англ. Laplace distribution [9]).