Сегментация изображений — различия между версиями
(→Введение) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 51 промежуточная версия 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Сегментация изображения - | + | '''Сегментация изображения''' {{---}} задача поиска групп пикселей, каждая из которых характеризует один смысловой объект. В статистике эта проблема известна как кластерный анализ и является широко изученной областью с сотнями различных алгоритмов. В компьютерном зрении сегментация изображения является одной из старейших и широко изучаемых проблем. |
| − | В более ранних техниках используется ''расщепление'' и ''слияние'' регионов, что соответствует ''разделительным'' и ''агломерационным'' алгоритмам в литературе по кластеризации. Современные алгоритмы чаще оптимизируют некоторые глобальные критерии, такие как внутрирегиональная согласованность и межрегиональные длины границ. | + | В более ранних техниках используется ''расщепление'' и ''слияние'' регионов, что соответствует ''разделительным'' и ''агломерационным'' алгоритмам в литературе по [[Кластеризация|кластеризации]]. Современные алгоритмы чаще оптимизируют некоторые глобальные критерии, такие как внутрирегиональная согласованность и межрегиональные длины границ. |
| − | + | Ниже будут рассмотрены два алгоритма {{---}} графо-ориентированная сегментация и метод нормализованных срезов. Первый из них является базовым алгоритмом сегментации, который прост и понятен в реализации, но медленный и результаты недостаточно хороши. Второй алгоритм является продвинутой версией первого со множеством эвристик. Что отражается, как на производительности, так и на результатах. | |
| − | Это алгоритм объединения, который использует относительные различия между регионами, чтобы определить, какие из них следует объединить. Кроме того, он доказуемо оптимизирует глобальную метрику группировки. Введем ''меру отличия'' одного пикселя от другого <tex>w(e)</tex>, | + | == Графо-ориентированная сегментация (англ. Graph-based segmentation) == |
| + | |||
| + | Это алгоритм объединения, который использует относительные различия между регионами, чтобы определить, какие из них следует объединить. Кроме того, он доказуемо оптимизирует глобальную метрику группировки. Введем ''меру отличия'' одного пикселя от другого <tex>w(e)</tex>, где <tex>e = (v_1, v_2)</tex> {{---}} пара соседних по стороне или по углу пикселей. ''Мера отличия'' может показывать, например, разницу цветовой интенсивности между соседями, которых у пикселя максимум восемь. | ||
Для любого региона ''R'', его внутренняя разница определяется как наибольшая ''мера отличия'' в минимальном остовном дереве региона, | Для любого региона ''R'', его внутренняя разница определяется как наибольшая ''мера отличия'' в минимальном остовном дереве региона, | ||
| − | <br><center><tex>Int(R) = \displaystyle\min_{e \in MST(R)} w(e) | + | <br><center><tex>Int(R) = \displaystyle\min_{e \in MST(R)} w(e)</tex></center>, |
Для любых двух соседних областей, по крайней мере, с одним смежным ребром, соединяющим их вершины, разность между этими регионами определяется как ребро минимального веса, соединяющее эти два региона, | Для любых двух соседних областей, по крайней мере, с одним смежным ребром, соединяющим их вершины, разность между этими регионами определяется как ребро минимального веса, соединяющее эти два региона, | ||
| − | <br><center><tex>Dif(R_1, R_2) = \displaystyle\min_{e = (v_1, v_2) | v_1 \in R_1, v_2 \in R_2} w(e) | + | <br><center><tex>Dif(R_1, R_2) = \displaystyle\min_{e = (v_1, v_2) | v_1 \in R_1, v_2 \in R_2} w(e)</tex></center>, |
Алгоритм объединяет любые две соседние области, разница которых меньше минимальной внутренней разности этих двух областей, | Алгоритм объединяет любые две соседние области, разница которых меньше минимальной внутренней разности этих двух областей, | ||
<br><center><tex>MInt(R_1, R_2) = \min(Int(R_1) + \tau(R_1), Int(R_2) +\tau(R_2)),</tex></center> | <br><center><tex>MInt(R_1, R_2) = \min(Int(R_1) + \tau(R_1), Int(R_2) +\tau(R_2)),</tex></center> | ||
| − | где <tex>\tau(R)</tex> - | + | где <tex>\tau(R)</tex> {{---}} эвристический штраф по региону, который был установлен <tex>k / |R|</tex>, однако, он может быть установлен как любая специфическая для области применения мера. |
| + | |||
| + | Объединяя области в порядке убывания разделяющих их ребер (можно эффективно оценить с использованием алгоритма минимального остовного дерева Крускала), они доказуемо дают сегментацию. Причем такую, в которой присутствуют как области, которые могли бы быть объединены, так и те, которые могут быть разделены, но в небольших количествах. Для окрестностей пикселей фиксированного размера время работы этого алгоритма составляет <tex>O (N \log N)</tex>, где <tex>N</tex> {{---}} количество пикселей изображения, что делает его одним из самых быстрых алгоритмов сегментации. | ||
| + | <br><center>[[Файл:beforeAfterGraphBased.png|800px|thumb|center|Источник: Felzenszwalb, P. F. and Huttenlocher, D. P. «Efficient graph-based image segmentation.»[http://people.cs.uchicago.edu/~pff/papers/seg-ijcv.pdf]]]</center> | ||
| + | <br>На рисунке слева {{---}} исходное изображение, справа {{---}} сегментированное после применения данного алгоритма. | ||
| + | |||
| + | == Метод нормализованных срезов (англ. Normalized cuts) == | ||
| + | |||
| + | Mетод нормализованных срезов, исследует сходство между соседними пикселями и пытается разделить их на группы, которые в свою очередь связаны слабо. | ||
| + | Рассмотрим простой пример. | ||
| + | [[Файл:graphNormalizedCut.png|800px|thumb|center|Источник: Richard Szeliski «Computer Vision: Algorithms and Applications.»[http://szeliski.org/Book/drafts/SzeliskiBook_20100903_draft.pdf]]] | ||
| + | <br>Все пиксели в группе A имеют высокое сходство, показанное в виде толстых красных линий, как и пиксели в группе B. Соединения между этими двумя группами, показанные в виде более тонких синих линий, намного слабее. ''Нормализованный разрез'' между двумя группами, показанный пунктирной линией, разделяет их на два кластера. | ||
| + | |||
| + | Разрез между двумя группами A и B определяется как сумма всех взвешенных весов, | ||
| + | <br><center><tex>cut(A, B) = \displaystyle\sum_{i \in A, j \in B}w_{ij},</tex></center> | ||
| + | где веса между двумя пикселями <tex>i</tex> и <tex>j</tex> соответствуют их сходству. Однако использование минимального среза в качестве критерия сегментации не приводит к разумным кластерам, поскольку наименьшие срезы обычно предусматривают выделение одного пикселя. | ||
| + | |||
| + | Лучшей мерой сегментации является нормализованный срез, который определяется как | ||
| + | <br><center><tex>Ncut(A,B)=\frac{cut(A,B)}{assoc(A, V)}+\frac{cut(A,B)}{assoc(B,V)},</tex></center> | ||
| + | где <tex>assoc(A,A)=\sum_{i \in A, j \in A}w_{ij}</tex> это ''ассоциация'' (сумма всех весов) в кластере и <tex>assoc(A,V)=assoc(A,A)+cut(A,B)</tex> это сумма всех весов ассоциированных с <tex>А</tex>. | ||
| + | <br>Нормализованные разрезы могут быть довольно медленными, поскольку это требует решения больших разреженных задач. Однако существует способ ускорить вычисление нормализованных разрезов, используя подход, основанный на алгебраической сетке. Можно выбирать меньшее количество переменных, чтобы оставшиеся переменные более нижнего уровня были ''сильно связаны'' по крайней мере с одной переменной грубого уровня. Подмножество <tex>C \subset V</tex> считается ''сильно связанным'', если выполняется | ||
| + | <br><center><tex>\frac{\sum_{j \in C}w_{ij}}{\sum_{j \in V}w_{ij}} > \phi, [*]</tex></center> | ||
| + | обычно <tex>\phi = 0.2.</tex> Данный рисунок схематично показывает этот процесс. | ||
| + | |||
| + | [[Файл:grephEdges.png|880px|thumb|center|''на первом изображении'' {{---}} исходная пиксельная сетка черно-белого изображения; ''на втором'' {{---}} межпиксельные связи, где более толстые линии указывают на более сильные связи; ''на третьем'' {{---}} сетка после одного уровня огрубления, когда каждый исходный пиксель сильно связан с одним из узлов грубого уровня; ''на четвертом'' {{---}} после двух уровней огрубления. Источник: Shaw, D. and Barnes, N. «Perspective rectangle detection. In Workshop on Applications of Computer Vision.» [https://www.researchgate.net/publication/6975028_Hierarchy_and_adaptivity_in_segmenting_visual_scenes]]] | ||
| + | |||
| + | Каждый пиксель на первом изображении соответствует вершине графа на втором изображении, которая связана с каждым из ее четырех соседей в соответствии с их сходством по уровню яркости. Цель состоит в том, чтобы «разрезать» этот граф на части. Далее можно найти ''сильно связное'' подмножество, которое минимизирует отношение <tex>[*]</tex>. Но несмотря на свою концептуальную значимость, минимизация этого ''нормализованного разреза'' является вычислительно непомерной, а стоимость увеличивается экспоненциально с размером изображения. Приближения к оптимальному разрезу могут быть получены с использованием спектральных методов, при этом наиболее эффективное на сегодняшний день приближение имеет вычислительную стоимость, пропорциональную <tex>n^{\frac{2}{3}}</tex>, где <tex>n</tex> {{---}} количество пикселей. Эта сверхлинейная сложность может быть чрезвычайно полезна, когда дело касается очень больших изображений. | ||
| + | |||
| + | Так как количество вершин графа на втором изображении велико и работать с каждым из них чрезвычайно дорого, необходимо выделить подмножество вершин-предводителей для каждого из подмножеств и далее работать уже с ними. Мы начнем с выбора примерно половины пикселей в качестве представителей, которые назовем ''начальными числами'': они выбираются таким образом, чтобы каждый пиксель в исходном изображении был ''сильно связан'' по крайней мере с одним соседним с ним ''начальным числом'' (см. третье изображение). Далее процесс продолжается рекурсивно (см. четвертое изображение), количество вершин на каждом новом более грубом уровне уменьшается. Значения узлов более нижнего уровня вычисляются путем интерполяции родительских значений и сопоставления значений <tex> \epsilon = 0,1</tex> в пределах от 0 и 1 до Boolean значений. Выраженные сегменты появляются на соответствующем уровне как узлы, которые слабо связаны со своими соседями. Следовательно, задача минимизации упрощается до поиска вершин-предводителей на всех уровнях. | ||
| + | |||
| + | Результат работы данного алгоритма: | ||
| + | [[Файл:watches.png|880px|thumb|center|Источник: Shaw, D. and Barnes, N. «Perspective rectangle detection. In Workshop on Applications of Computer Vision.» [https://www.researchgate.net/publication/6975028_Hierarchy_and_adaptivity_in_segmenting_visual_scenes]]] | ||
| + | |||
| + | == Свёрточные нейронные сети == | ||
| + | |||
| + | [[Файл:SegmentationExample.jpeg|300px|thumb|right|Пример семантической сегментации изображения]] | ||
| + | |||
| + | С учётом прогресса глубоких нейронных сетей за последние несколько лет в различных областях, лучшие результаты для семантической сегментации чаще всего достигаются при помощи [[:Сверточные_нейронные_сети|свёрточных нейронных сетей]], в том числе, когда данные [https://arxiv.org/abs/1502.02734 слабо размечены]. Действительно, проблема низкого уровня размеченности данных в семантической сегментации довольно важна, поскольку для каждого пикселя определить его принадлежность с высокой точностью {{---}} задача, требующая высоких затрат времени и не всегда высокую точность. Однако, сочетание хорошо размеченных данных со слабо размеченными данными (например, с точностью до ограничивающих рамок) улучшает производительность модели. Для задачи сегментации [https://arxiv.org/abs/1605.06211 хорошо себя показали] FCN (англ. fully-convolutional networks) {{---}} полносвёрточные сети, позволяющие работать с изображениями произвольного размера, а на выходе выдавать тепловую карту нахождения классов на изображении через серию свёрток. Поскольку свёртка над матрицей большой размерности с большим числом каналом является затратной, как правило, первая половина слоёв в таких свёрточных сетях обеспечивает сабсэмплинг (англ. subsampling - уменьшение размерности), а вторая часть слоёв - апсэмплинг (англ. upsampling - увеличение размерности). Таким образом, размерность изображений в пикселях на входе и на выходе сети является одинаковой, а большинство операций свёртки применяется к матрицам небольшой размерности. Конечная классификация достигается за счёт выбора максимума по классам из значений тензора размерности $C \times W \times H$, где $C$ {{---}} множество классов, заранее заданных перед обучением и к которым могут принадлежать пиксели изображения, $W \times H$ {{---}} размер изображения. Такую модель можно обучить при помощи [[:Обратное_распространение_ошибки|обратного распространения ошибок]], а в качестве функции потерь для пикселей использовать кросс-энтропию. | ||
| + | |||
| + | Модель [https://arxiv.org/abs/1505.04597 U-Net], разработанная авторами для сегментации биомедицинских изображений, улучшает архитектуру FCN путём использования сужающихся блоков свёртки для захвата контекста, расширяющихся блоков свёртки для локализации, а также прямых связей между блоками свёртки на одинаковых уровнях. Прямая связь слоёв обеспечивает улучшенное обучение за счёт отсутствия так называемого "артефакта шахматной доски" {{---}} негативного явления, вызванного апсэмплингом при помощи транспонированной свёртки. Развитием U-Net, в свою очередь модель [https://arxiv.org/abs/1611.09326 DenseNet], в которой используются полностью связанные свёрточные сети. В основе идеи лежит использование "плотных блоков" {{---}} совокупности нескольких свёрточных слоёв с подключением каждого слоя к каждому слою. Однако, существенным недостатком такой модели является низкая эффективность работы с памятью. | ||
| + | |||
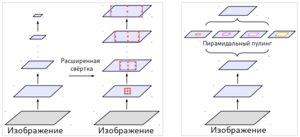
| + | Совершенно по-иному на свёртку для сегментации объектов позволил взглянуть метод расширенных свёрток (англ. atrous convolutions), применяющийся в современных state-of-the-art подходах ([https://arxiv.org/abs/1606.00915 DeepLab], [https://arxiv.org/abs/1706.05587 DeepLab v3], [https://paperswithcode.com/paper/encoder-decoder-with-atrous-separable DeepLab v3+]). Расширенная свёртка заключается в том, чтобы применять свёртки с ядрами разного размера и разным страйдом над прямоугольниками с одним и тем же центром, а впоследствии комбинировать полученные таким образом признаки. Расширенные свёртки могут применяться как каскадно (последовательно регулируя показатель расширения фильтра), так и параллельно (англ. ASPP, Atrous Spatial Pyramid Pooling {{---}} применяя свёртки с различным масштабом ядер на одном и том же слое свёрточной сети с пулингом в конце). Такой подход позволил достичь лучших результатов в изображениях с объектами разных масштабов. | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:U-Net-RUS.png|300px|thumb|Архитектура слоёв свёртки U-Net]] | ||
| + | |[[Файл:AtrousConvolution-RUS.png|300px|thumb|Расширенная свёртка (atrous convolution) и пространственный пирамидальный пулинг (ASPP)]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | == См. также == | ||
| + | |||
| + | [[Задача нахождения объектов на изображении]] | ||
| + | |||
| + | == Источники информации == | ||
| + | |||
| + | * Richard Szeliski «Computer Vision: Algorithms and Applications.» - «Springer», 2010. - С. 286-300 | ||
| + | * Felzenszwalb, P. F. and Huttenlocher, D. P. (2004b). Efficient graph-based image segmentation.[http://people.cs.uchicago.edu/~pff/papers/seg-ijcv.pdf] | ||
| + | * Shaw, D. and Barnes, N. (2006). Perspective rectangle detection. In Workshop on Applications of Computer Vision at ECCV’2006. | ||
| + | * Brandt, A. (1986). Algebraic multigrid theory: The symmetric case. Applied Mathematics and Computation, 19(1-4):23–56. | ||
| − | + | [[Категория: Машинное обучение]] | |
| − | + | [[Категория: Компьютерное зрение]] | |
| − | |||
Текущая версия на 19:03, 4 сентября 2022
Сегментация изображения — задача поиска групп пикселей, каждая из которых характеризует один смысловой объект. В статистике эта проблема известна как кластерный анализ и является широко изученной областью с сотнями различных алгоритмов. В компьютерном зрении сегментация изображения является одной из старейших и широко изучаемых проблем.
В более ранних техниках используется расщепление и слияние регионов, что соответствует разделительным и агломерационным алгоритмам в литературе по кластеризации. Современные алгоритмы чаще оптимизируют некоторые глобальные критерии, такие как внутрирегиональная согласованность и межрегиональные длины границ.
Ниже будут рассмотрены два алгоритма — графо-ориентированная сегментация и метод нормализованных срезов. Первый из них является базовым алгоритмом сегментации, который прост и понятен в реализации, но медленный и результаты недостаточно хороши. Второй алгоритм является продвинутой версией первого со множеством эвристик. Что отражается, как на производительности, так и на результатах.
Содержание
Графо-ориентированная сегментация (англ. Graph-based segmentation)
Это алгоритм объединения, который использует относительные различия между регионами, чтобы определить, какие из них следует объединить. Кроме того, он доказуемо оптимизирует глобальную метрику группировки. Введем меру отличия одного пикселя от другого , где — пара соседних по стороне или по углу пикселей. Мера отличия может показывать, например, разницу цветовой интенсивности между соседями, которых у пикселя максимум восемь.
Для любого региона R, его внутренняя разница определяется как наибольшая мера отличия в минимальном остовном дереве региона,
Для любых двух соседних областей, по крайней мере, с одним смежным ребром, соединяющим их вершины, разность между этими регионами определяется как ребро минимального веса, соединяющее эти два региона,
Алгоритм объединяет любые две соседние области, разница которых меньше минимальной внутренней разности этих двух областей,
где — эвристический штраф по региону, который был установлен , однако, он может быть установлен как любая специфическая для области применения мера.
Объединяя области в порядке убывания разделяющих их ребер (можно эффективно оценить с использованием алгоритма минимального остовного дерева Крускала), они доказуемо дают сегментацию. Причем такую, в которой присутствуют как области, которые могли бы быть объединены, так и те, которые могут быть разделены, но в небольших количествах. Для окрестностей пикселей фиксированного размера время работы этого алгоритма составляет , где — количество пикселей изображения, что делает его одним из самых быстрых алгоритмов сегментации.

На рисунке слева — исходное изображение, справа — сегментированное после применения данного алгоритма.
Метод нормализованных срезов (англ. Normalized cuts)
Mетод нормализованных срезов, исследует сходство между соседними пикселями и пытается разделить их на группы, которые в свою очередь связаны слабо. Рассмотрим простой пример.
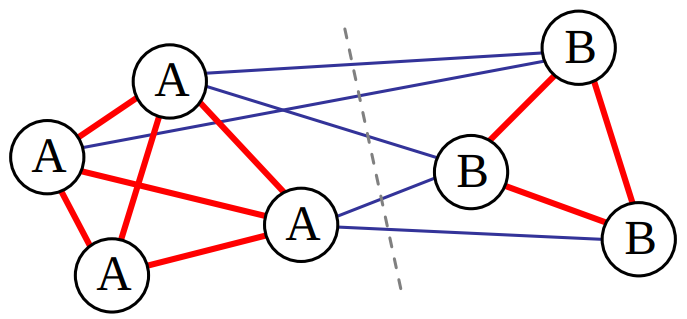
Все пиксели в группе A имеют высокое сходство, показанное в виде толстых красных линий, как и пиксели в группе B. Соединения между этими двумя группами, показанные в виде более тонких синих линий, намного слабее. Нормализованный разрез между двумя группами, показанный пунктирной линией, разделяет их на два кластера.
Разрез между двумя группами A и B определяется как сумма всех взвешенных весов,
где веса между двумя пикселями и соответствуют их сходству. Однако использование минимального среза в качестве критерия сегментации не приводит к разумным кластерам, поскольку наименьшие срезы обычно предусматривают выделение одного пикселя.
Лучшей мерой сегментации является нормализованный срез, который определяется как
где это ассоциация (сумма всех весов) в кластере и это сумма всех весов ассоциированных с .
Нормализованные разрезы могут быть довольно медленными, поскольку это требует решения больших разреженных задач. Однако существует способ ускорить вычисление нормализованных разрезов, используя подход, основанный на алгебраической сетке. Можно выбирать меньшее количество переменных, чтобы оставшиеся переменные более нижнего уровня были сильно связаны по крайней мере с одной переменной грубого уровня. Подмножество считается сильно связанным, если выполняется
обычно Данный рисунок схематично показывает этот процесс.
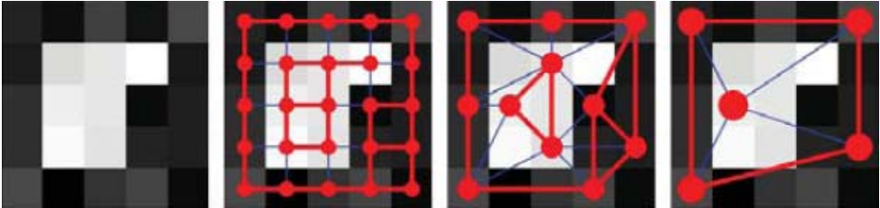
Каждый пиксель на первом изображении соответствует вершине графа на втором изображении, которая связана с каждым из ее четырех соседей в соответствии с их сходством по уровню яркости. Цель состоит в том, чтобы «разрезать» этот граф на части. Далее можно найти сильно связное подмножество, которое минимизирует отношение . Но несмотря на свою концептуальную значимость, минимизация этого нормализованного разреза является вычислительно непомерной, а стоимость увеличивается экспоненциально с размером изображения. Приближения к оптимальному разрезу могут быть получены с использованием спектральных методов, при этом наиболее эффективное на сегодняшний день приближение имеет вычислительную стоимость, пропорциональную , где — количество пикселей. Эта сверхлинейная сложность может быть чрезвычайно полезна, когда дело касается очень больших изображений.
Так как количество вершин графа на втором изображении велико и работать с каждым из них чрезвычайно дорого, необходимо выделить подмножество вершин-предводителей для каждого из подмножеств и далее работать уже с ними. Мы начнем с выбора примерно половины пикселей в качестве представителей, которые назовем начальными числами: они выбираются таким образом, чтобы каждый пиксель в исходном изображении был сильно связан по крайней мере с одним соседним с ним начальным числом (см. третье изображение). Далее процесс продолжается рекурсивно (см. четвертое изображение), количество вершин на каждом новом более грубом уровне уменьшается. Значения узлов более нижнего уровня вычисляются путем интерполяции родительских значений и сопоставления значений в пределах от 0 и 1 до Boolean значений. Выраженные сегменты появляются на соответствующем уровне как узлы, которые слабо связаны со своими соседями. Следовательно, задача минимизации упрощается до поиска вершин-предводителей на всех уровнях.
Результат работы данного алгоритма:

Свёрточные нейронные сети
С учётом прогресса глубоких нейронных сетей за последние несколько лет в различных областях, лучшие результаты для семантической сегментации чаще всего достигаются при помощи свёрточных нейронных сетей, в том числе, когда данные слабо размечены. Действительно, проблема низкого уровня размеченности данных в семантической сегментации довольно важна, поскольку для каждого пикселя определить его принадлежность с высокой точностью — задача, требующая высоких затрат времени и не всегда высокую точность. Однако, сочетание хорошо размеченных данных со слабо размеченными данными (например, с точностью до ограничивающих рамок) улучшает производительность модели. Для задачи сегментации хорошо себя показали FCN (англ. fully-convolutional networks) — полносвёрточные сети, позволяющие работать с изображениями произвольного размера, а на выходе выдавать тепловую карту нахождения классов на изображении через серию свёрток. Поскольку свёртка над матрицей большой размерности с большим числом каналом является затратной, как правило, первая половина слоёв в таких свёрточных сетях обеспечивает сабсэмплинг (англ. subsampling - уменьшение размерности), а вторая часть слоёв - апсэмплинг (англ. upsampling - увеличение размерности). Таким образом, размерность изображений в пикселях на входе и на выходе сети является одинаковой, а большинство операций свёртки применяется к матрицам небольшой размерности. Конечная классификация достигается за счёт выбора максимума по классам из значений тензора размерности $C \times W \times H$, где $C$ — множество классов, заранее заданных перед обучением и к которым могут принадлежать пиксели изображения, $W \times H$ — размер изображения. Такую модель можно обучить при помощи обратного распространения ошибок, а в качестве функции потерь для пикселей использовать кросс-энтропию.
Модель U-Net, разработанная авторами для сегментации биомедицинских изображений, улучшает архитектуру FCN путём использования сужающихся блоков свёртки для захвата контекста, расширяющихся блоков свёртки для локализации, а также прямых связей между блоками свёртки на одинаковых уровнях. Прямая связь слоёв обеспечивает улучшенное обучение за счёт отсутствия так называемого "артефакта шахматной доски" — негативного явления, вызванного апсэмплингом при помощи транспонированной свёртки. Развитием U-Net, в свою очередь модель DenseNet, в которой используются полностью связанные свёрточные сети. В основе идеи лежит использование "плотных блоков" — совокупности нескольких свёрточных слоёв с подключением каждого слоя к каждому слою. Однако, существенным недостатком такой модели является низкая эффективность работы с памятью.
Совершенно по-иному на свёртку для сегментации объектов позволил взглянуть метод расширенных свёрток (англ. atrous convolutions), применяющийся в современных state-of-the-art подходах (DeepLab, DeepLab v3, DeepLab v3+). Расширенная свёртка заключается в том, чтобы применять свёртки с ядрами разного размера и разным страйдом над прямоугольниками с одним и тем же центром, а впоследствии комбинировать полученные таким образом признаки. Расширенные свёртки могут применяться как каскадно (последовательно регулируя показатель расширения фильтра), так и параллельно (англ. ASPP, Atrous Spatial Pyramid Pooling — применяя свёртки с различным масштабом ядер на одном и том же слое свёрточной сети с пулингом в конце). Такой подход позволил достичь лучших результатов в изображениях с объектами разных масштабов.
См. также
Задача нахождения объектов на изображении
Источники информации
- Richard Szeliski «Computer Vision: Algorithms and Applications.» - «Springer», 2010. - С. 286-300
- Felzenszwalb, P. F. and Huttenlocher, D. P. (2004b). Efficient graph-based image segmentation.[5]
- Shaw, D. and Barnes, N. (2006). Perspective rectangle detection. In Workshop on Applications of Computer Vision at ECCV’2006.
- Brandt, A. (1986). Algebraic multigrid theory: The symmetric case. Applied Mathematics and Computation, 19(1-4):23–56.