Виды ансамблей — различия между версиями
(→Вероятность ошибки: Графики, которые нужно после вставить) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 60 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
== Ансамбль == | == Ансамбль == | ||
| − | Рассмотрим задачу классификации на K классов: <tex>Y = \{1, 2, ..., K\}</tex> <br> | + | Ансамбль алгоритмов (методов) — метод, который использует несколько обучающих алгоритмов с целью получения лучшей эффективности прогнозирования, чем можно было бы получить от каждого обучающего алгоритма по отдельности. |
| − | Пусть имеется M | + | |
| − | <tex> f_m : X \ | + | Рассмотрим задачу классификации на <tex> K </tex> классов: <tex>Y = \{1, 2, ..., K\}</tex>. <br> |
| + | Пусть имеется <tex> M </tex> классификаторов ("экспертов"): <tex> f_1, f_2, ..., f_M </tex>. <br> | ||
| + | <tex> f_m : X \rightarrow Y, f_m \in F, m = (1 ... M) </tex>. <br> | ||
Тогда давайте посмотрим новый классификатор на основе данных: | Тогда давайте посмотрим новый классификатор на основе данных: | ||
| − | Простое голосование: <tex> f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M I(f_i(x) = k) </tex> <br> | + | Простое голосование: <tex> f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M I(f_i(x) = k) </tex>. <br> |
| − | Взвешенное голосование: <tex> f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M \alpha_i I(f_i(x) = k), \sum \limits_i \alpha_i = 1, \alpha_i > 0</tex> | + | Взвешенное голосование: <tex> f(x) = \max \limits_{k = 1 .. K} \sum \limits_{i = 1}^M \alpha_i I(f_i(x) = k), \sum \limits_i \alpha_i = 1, \alpha_i > 0</tex>. <br> |
| + | Где <tex> \begin{equation*} | ||
| + | I(x) = \begin{cases} | ||
| + | 1 &\text{x = true}\\ | ||
| + | 0 &\text{x = false} | ||
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | </tex> | ||
| + | |||
| + | == Теорема Кондорсе о присяжных == | ||
| − | = | + | {{Теорема |
| + | |statement= | ||
| + | Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри, и стремится к единице. <br> | ||
| + | Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных. | ||
| + | }} | ||
| − | Пусть <tex>M</tex> | + | Пусть <tex>M</tex> — количество присяжных, <tex>p</tex> — вероятность правильного решения одного эксперта, <tex>R</tex> — вероятность правильного решения всего жюри, |
| − | <tex>m</tex> | + | <tex>m</tex> — минимальное большинство членов жюри <tex> = \lfloor \frac N 2 \rfloor + 1 </tex>. |
Тогда <tex> R = \sum \limits_{i = m}^M C_M^i p ^ i (1 - p) ^ {M - i} </tex> | Тогда <tex> R = \sum \limits_{i = m}^M C_M^i p ^ i (1 - p) ^ {M - i} </tex> | ||
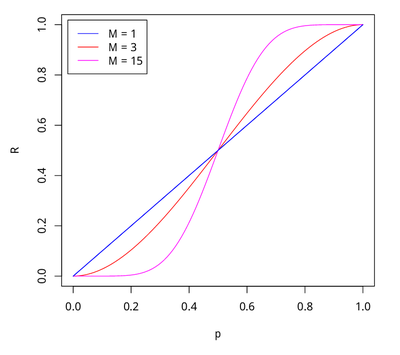
| − | + | [[Файл:Виды_Ансамблей_2.png|none|400px|thumb|Вероятность правильного решения всего жюри (R) в зависимости от вероятности правильного решения одного эксперта (p) при разном количестве экспертов(M)]] | |
| − | + | ||
| + | == Бэггинг == | ||
| + | |||
| + | Пусть имеется выборка <tex>X</tex> размера <tex>N</tex>. Количество классификаторов <tex>M</tex>. | ||
| + | |||
| + | Алгоритм использует метод бутстрэпа (англ. ''bootstrap''): | ||
| + | |||
| + | Из всего множества объектов равновероятно выберем N объектов с возвращением. Это значит, что после выбора каждого из объектов мы будем возращать его в множество для выбора. Отметим, что из-за возвращения некоторые объекты могут повторяться в выбранном множестве.<br> Обозначим новую выборку через <tex>X_1</tex>. Повторяя процедуру <tex>M</tex> раз, сгенерируем <tex>M</tex> подвыборок <tex>X_1 ... X_M</tex>. Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения. | ||
| + | |||
| + | Шаги алгоритма бэггинг: | ||
| + | <ul> | ||
| + | <li> Генерируется с помощью бутстрэпа M выборок размера N для каждого классификатора. | ||
| + | <li> Производится независимое обучения каждого элементарного классификатора (каждого алгоритма, определенного на своем подпространстве). | ||
| + | <li> Производится классификация основной выборки на каждом из подпространств (также независимо). | ||
| + | <li> Принимается окончательное решение о принадлежности объекта одному из классов. Это можно сделать несколькими разными способами, подробнее описано ниже. | ||
| + | </ul> | ||
| + | |||
| + | |||
| + | Окончательное решение о принадлежности объекта классу может приниматься, например, одним из следующих методов: | ||
| + | <ul> | ||
| + | <li> Консенсус: если все элементарные классификаторы присвоили объекту одну и ту же метку, то относим объект к выбранному классу. | ||
| + | <li> Простое большинство: консенсус достижим очень редко, поэтому чаще всего используют метод простого большинства. Здесь объекту присваивается метка того класса, который определило для него большинство элементарных классификаторов. | ||
| + | <li> Взвешивание классификаторов: если классификаторов четное количество, то голосов может получиться поровну, еще возможно, что для экспертов одна из групп параметров важна в большей степени, тогда прибегают к взвешиванию классификаторов. То есть при голосовании голос классификатора умножается на его вес. | ||
| + | </ul> | ||
| + | |||
| + | [[Файл:Виды_ансамблей_Бэггинг_рус.png|none|800px]] | ||
| + | |||
| + | |||
| + | Рассмотрим задачу регрессии с базовыми алгоритмами <tex>b_1, b_2, ..., b_m</tex>. Предположим, что существует истинная функция ответа для всех объектов y(x), а также задано распределение p(x) на объектах. В этом случае мы можем записать ошибку каждой функции регрессии: | ||
| + | |||
| + | <tex> \epsilon_i(x) = b_i(x) - y(x), y = 1, ..., n </tex> | ||
| + | |||
| + | и записать матожидание среднеквадратичной ошибки: | ||
| + | |||
| + | <tex>E_x(b_i(x) - y(x))^2 = E_x \epsilon_i^2(x) </tex> | ||
| + | |||
| + | Средняя ошибка построенных функций регрессии имеет вид: | ||
| + | |||
| + | <tex>E_1 = \frac 1 n E_x \sum \limits_{i = 1}^n \epsilon_i^2(x) </tex> | ||
| + | |||
| + | Предположим, что ошибки несмещены и некоррелированы: | ||
| + | |||
| + | <tex> E_x\epsilon_i(x) = 0, E_x\epsilon_i(x)\epsilon_j(x) = 0, i ≠ j </tex> | ||
| + | |||
| + | Построим теперь новую функцию регрессии, усредняющую ответы уже построенных: | ||
| + | |||
| + | <tex> a(x) = \frac 1 n \sum \limits_{i = 1}^n b_i(x) </tex> | ||
| + | |||
| + | Найдем ее среднеквадратичную ошибку: | ||
| + | |||
| + | <tex> E_n = E_x(\frac 1 n \sum \limits_{i = 1}^n (b_i(x) - y(x))^2 | ||
| + | = E_x(\frac 1 n \sum \limits_{i = 1}^n \epsilon_i)^2 | ||
| + | = \frac 1 {n^2} E_x(\sum \limits_{i = 1}^n \epsilon_i^2(x) + \sum \limits_{i ≠ j} \epsilon_i(x)\epsilon_j(x)) | ||
| + | = \frac 1 n E_1 </tex> | ||
| + | |||
| + | Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в <tex>n</tex> раз. | ||
| + | |||
| + | == Бустинг == | ||
| + | |||
| + | [[Бустинг, AdaBoost|'''Бустинг''']] (англ. boosting — улучшение) — это процедура последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов. Бустинг представляет собой жадный алгоритм построения композиции алгоритмов. | ||
| + | |||
| + | Пусть <tex>h(x, a)</tex> — базовый классификатор, где <tex>a</tex> — вектор параметров. | ||
| + | |||
| + | Задача состоит в том, чтоб найти такой алгоритм <tex>H_T(x) = \sum_{t=1}^T b_t h(x, a),</tex> где <tex>b_t \in \mathbb{R}</tex> — коэффиценты, такие, чтобы минимизировать эмпирический риск <tex>Q = \sum_i L(H_T(x_i), y_i) \rightarrow min</tex>, где <tex>L(H_T(x_i), y_i)</tex> — функция потерь. | ||
| + | |||
| + | Очевидно, что сложно найти сразу <tex>\{(a_t, b_t)\}_{t=1}^T.</tex> Основная идея в том, чтоб найти решение пошагово <tex>H_t(x) = H_{t — 1}(x) + b_t h(x, a_t)</tex>. Таким образом мы сможем постепенно оценивать изменение эмпирического риска <tex>Q^{(t)} = \sum_{i = 1}^l L(H_t(x_i), y_i) </tex>. | ||
| + | |||
| + | Алгоритмы бустинга: | ||
| + | |||
| + | <ul> | ||
| + | <li>[[Бустинг, AdaBoost|AdaBoost]] — адаптивный алгоритм бустинга, усиливающий классификаторы, объединяя их в «комитет». Чувствителен к шуму. | ||
| + | <li>BrownBoost — алгоритм бустинга, эффективный на зашумленных наборах данных | ||
| + | <li>GradientBoost — алгоритм бустинга, использующий идеи линейной регресии | ||
| + | <li>LogitBoost — алгоритм бустинга, использующий идеи логистической регресси | ||
| + | </ul> | ||
| + | |||
| + | == Реализации и применения бустинга == | ||
| + | |||
| + | Реализации бустинга: | ||
| + | |||
| + | * [[XGBoost|XGBoost]] — одна из самых популярных и эффективных реализаций алгоритма градиентного бустинга на деревьях на 2019-й год. | ||
| + | * [[CatBoost|CatBoost]] — открытая программная библиотека, разработанная компанией Яндекс. | ||
| + | * LightGBM — библиотека для метода машинного обучения, основанная на градиентном бустинге (англ. gradient boosting). | ||
| + | |||
| + | |||
| + | Применение бустинга: | ||
| + | * поисковые системы | ||
| + | * ранжирования ленты рекомендаций | ||
| + | * прогноз погоды | ||
| + | * оптимизации расхода сырья | ||
| + | * предсказания дефектов при производстве. | ||
| + | * исследованиях на Большом адронном коллайдере (БАК) для объединения информации с различных частей детектора LHCb в максимально точное, агрегированное знание о частице. | ||
| − | == | + | == Различия между алгоритмами == |
| − | |||
| − | == | + | <ul> |
| − | + | <li> Оба алгоритма используют N базовых классификаторов | |
| + | <ul> | ||
| + | <li> Бустинг использует последовательное обучение </li> | ||
| + | <li> Бэггинг использует параллельное обучение </li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | <li> Оба генерируют несколько наборов данных для обучения путем случайной выборки | ||
| + | <ul> | ||
| + | <li> Бустинг определяет вес данных, чтоб утяжелить тяжелые случаи </li> | ||
| + | <li> Бэггинг имеет невзвешенные данные </li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | <li> Оба принимают окончательное решение, усредняя N классификаторов | ||
| + | <ul> | ||
| + | <li> В бустинге определяются веса для них </li> | ||
| + | <li> В бэггинге они равнозначны </li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | <li> Оба уменьшают дисперсию и обеспечивают более высокую стабильность | ||
| + | <ul> | ||
| + | <li> Бэггинг может решить проблему переобучения </li> | ||
| + | <li> Бустинг пытается уменьшить смещение, но может увеличить проблему переобучения </li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | </ul> | ||
| + | |||
| + | == Примеры кода == | ||
| + | |||
| + | '''Инициализация''' | ||
| + | |||
| + | from pydataset import data | ||
| + | |||
| + | <font color="green">#Считаем данные The Boston Housing Dataset<ref>[http://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html The Boston Housing Dataset]</ref> </font> | ||
| + | df = data('Housing') | ||
| + | |||
| + | <font color="green">#Проверим данные</font> | ||
| + | df.head().values | ||
| + | array([[42000.0, 5850, 3, 1, 2, 'yes', 'no', 'yes', 'no', 'no', 1, 'no'], | ||
| + | [38500.0, 4000, 2, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'], | ||
| + | [49500.0, 3060, 3, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'], ... | ||
| + | |||
| + | <font color="green"># Создадим словарь для слов 'no', 'yes'</font> | ||
| + | d = dict(zip(['no', 'yes'], range(0,2))) | ||
| + | for i in zip(df.dtypes.index, df.dtypes): | ||
| + | if str(i[1]) == 'object': | ||
| + | df[i[0]] = df[i[0]].map(d) | ||
| + | df[‘price’] = pd.qcut(df[‘price’], 3, labels=[‘0’, ‘1’, ‘2’]).cat.codes | ||
| + | |||
| + | <font color="green"># Разделим множество на два</font> | ||
| + | y = df['price'] | ||
| + | X = df.drop('price', 1) | ||
| + | |||
| + | '''Бэггинг''' | ||
| + | |||
| + | <font color="green"># Импорты классификаторов</font> | ||
| + | from sklearn.model_selection import cross_val_score | ||
| + | from sklearn.ensemble import BaggingClassifier, ExtraTreesClassifier, RandomForestClassifier | ||
| + | from sklearn.neighbors import KNeighborsClassifier | ||
| + | from sklearn.linear_model import RidgeClassifier | ||
| + | from sklearn.svm import SVC | ||
| + | |||
| + | seed = 1075 | ||
| + | np.random.seed(seed) | ||
| + | <font color="green"># Инициализуруем классификаторы</font> | ||
| + | rf = RandomForestClassifier() | ||
| + | et = ExtraTreesClassifier() | ||
| + | knn = KNeighborsClassifier() | ||
| + | svc = SVC() | ||
| + | rg = RidgeClassifier() | ||
| + | clf_array = [rf, et, knn, svc, rg] | ||
| + | |||
| + | for clf in clf_array: | ||
| + | vanilla_scores = cross_val_score(clf, X, y, cv=10, n_jobs=-1) | ||
| + | bagging_clf = BaggingClassifier(clf, max_samples=0.4, max_features=10, random_state=seed) | ||
| + | bagging_scores = cross_val_score(bagging_clf, X, y, cv=10, n_jobs=-1) | ||
| + | print "Mean of: {1:.3f}, std: (+/-) {2:.3f [{0}]" | ||
| + | .format(clf.__class__.__name__, | ||
| + | vanilla_scores.mean(), vanilla_scores.std()) | ||
| + | print "Mean of: {1:.3f}, std: (+/-) {2:.3f} [Bagging {0}]\n" | ||
| + | .format(clf.__class__.__name__, | ||
| + | bagging_scores.mean(), bagging_scores.std()) | ||
| + | |||
| + | <font color="green">#Результат</font> | ||
| + | Mean of: 0.632, std: (+/-) 0.081 [RandomForestClassifier] | ||
| + | Mean of: 0.639, std: (+/-) 0.069 [Bagging RandomForestClassifier] | ||
| + | |||
| + | Mean of: 0.636, std: (+/-) 0.080 [ExtraTreesClassifier] | ||
| + | Mean of: 0.654, std: (+/-) 0.073 [Bagging ExtraTreesClassifier] | ||
| + | |||
| + | Mean of: 0.500, std: (+/-) 0.086 [KNeighborsClassifier] | ||
| + | Mean of: 0.535, std: (+/-) 0.111 [Bagging KNeighborsClassifier] | ||
| + | |||
| + | Mean of: 0.465, std: (+/-) 0.085 [SVC] | ||
| + | Mean of: 0.535, std: (+/-) 0.083 [Bagging SVC] | ||
| + | |||
| + | Mean of: 0.639, std: (+/-) 0.050 [RidgeClassifier] | ||
| + | Mean of: 0.597, std: (+/-) 0.045 [Bagging RidgeClassifier] | ||
| + | |||
| + | '''Бустинг''' | ||
| + | |||
| + | ada_boost = AdaBoostClassifier() | ||
| + | grad_boost = GradientBoostingClassifier() | ||
| + | xgb_boost = XGBClassifier() | ||
| + | boost_array = [ada_boost, grad_boost, xgb_boost] | ||
| + | eclf = EnsembleVoteClassifier(clfs=[ada_boost, grad_boost, xgb_boost], voting='hard') | ||
| + | |||
| + | labels = ['Ada Boost', 'Grad Boost', 'XG Boost', 'Ensemble'] | ||
| + | for clf, label in zip([ada_boost, grad_boost, xgb_boost, eclf], labels): | ||
| + | scores = cross_val_score(clf, X, y, cv=10, scoring='accuracy') | ||
| + | print("Mean: {0:.3f}, std: (+/-) {1:.3f} [{2}]".format(scores.mean(), scores.std(), label)) | ||
| + | |||
| + | <font color="green"># Результат</font> | ||
| + | Mean: 0.641, std: (+/-) 0.082 [Ada Boost] | ||
| + | Mean: 0.654, std: (+/-) 0.113 [Grad Boost] | ||
| + | Mean: 0.663, std: (+/-) 0.101 [XG Boost] | ||
| + | Mean: 0.667, std: (+/-) 0.105 [Ensemble] | ||
| + | |||
| + | == См. также == | ||
| + | * [[:Бустинг, AdaBoost|Бустинг, AdaBoost]] | ||
| + | * [[:XGBoost|XGBoost]] | ||
| + | * [[:CatBoost|CatBoost]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
| + | |||
| + | == Источники информации == | ||
| + | |||
| + | * https://github.com/Microsoft/LightGBM | ||
| + | * https://github.com/dmlc/xgboost | ||
| + | * https://ru.wikipedia.org/wiki/CatBoost | ||
| + | * https://quantdare.com/what-is-the-difference-between-bagging-and-boosting/ | ||
| + | * https://medium.com/@rrfd/boosting-bagging-and-stacking-ensemble-methods-with-sklearn-and-mlens-a455c0c982de | ||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Ансамбли]] | ||
Текущая версия на 19:15, 4 сентября 2022
Содержание
Ансамбль
Ансамбль алгоритмов (методов) — метод, который использует несколько обучающих алгоритмов с целью получения лучшей эффективности прогнозирования, чем можно было бы получить от каждого обучающего алгоритма по отдельности.
Рассмотрим задачу классификации на классов: .
Пусть имеется классификаторов ("экспертов"): .
.
Тогда давайте посмотрим новый классификатор на основе данных:
Простое голосование: .
Взвешенное голосование: .
Где
Теорема Кондорсе о присяжных
| Теорема: |
Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри, и стремится к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных. |
Пусть — количество присяжных, — вероятность правильного решения одного эксперта, — вероятность правильного решения всего жюри, — минимальное большинство членов жюри .
Тогда
Бэггинг
Пусть имеется выборка размера . Количество классификаторов .
Алгоритм использует метод бутстрэпа (англ. bootstrap):
Из всего множества объектов равновероятно выберем N объектов с возвращением. Это значит, что после выбора каждого из объектов мы будем возращать его в множество для выбора. Отметим, что из-за возвращения некоторые объекты могут повторяться в выбранном множестве.
Обозначим новую выборку через . Повторяя процедуру раз, сгенерируем подвыборок . Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.
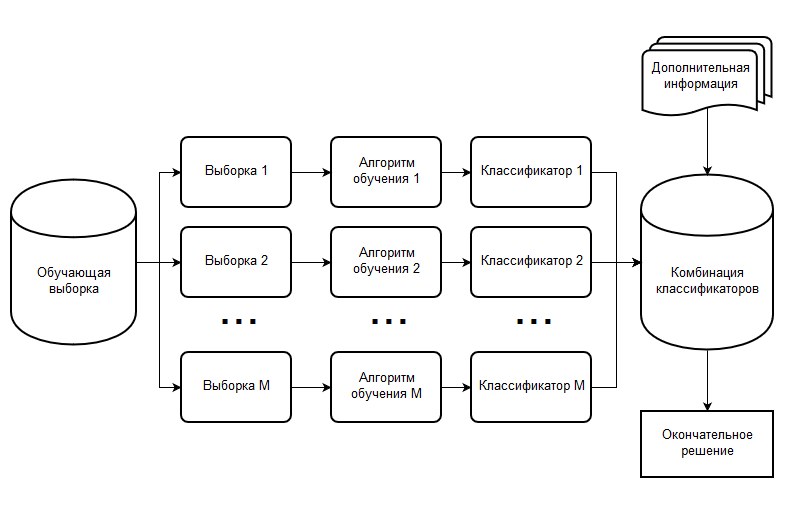
Шаги алгоритма бэггинг:
- Генерируется с помощью бутстрэпа M выборок размера N для каждого классификатора.
- Производится независимое обучения каждого элементарного классификатора (каждого алгоритма, определенного на своем подпространстве).
- Производится классификация основной выборки на каждом из подпространств (также независимо).
- Принимается окончательное решение о принадлежности объекта одному из классов. Это можно сделать несколькими разными способами, подробнее описано ниже.
Окончательное решение о принадлежности объекта классу может приниматься, например, одним из следующих методов:
- Консенсус: если все элементарные классификаторы присвоили объекту одну и ту же метку, то относим объект к выбранному классу.
- Простое большинство: консенсус достижим очень редко, поэтому чаще всего используют метод простого большинства. Здесь объекту присваивается метка того класса, который определило для него большинство элементарных классификаторов.
- Взвешивание классификаторов: если классификаторов четное количество, то голосов может получиться поровну, еще возможно, что для экспертов одна из групп параметров важна в большей степени, тогда прибегают к взвешиванию классификаторов. То есть при голосовании голос классификатора умножается на его вес.
Рассмотрим задачу регрессии с базовыми алгоритмами . Предположим, что существует истинная функция ответа для всех объектов y(x), а также задано распределение p(x) на объектах. В этом случае мы можем записать ошибку каждой функции регрессии:
и записать матожидание среднеквадратичной ошибки:
Средняя ошибка построенных функций регрессии имеет вид:
Предположим, что ошибки несмещены и некоррелированы:
Построим теперь новую функцию регрессии, усредняющую ответы уже построенных:
Найдем ее среднеквадратичную ошибку:
Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в раз.
Бустинг
Бустинг (англ. boosting — улучшение) — это процедура последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов. Бустинг представляет собой жадный алгоритм построения композиции алгоритмов.
Пусть — базовый классификатор, где — вектор параметров.
Задача состоит в том, чтоб найти такой алгоритм где — коэффиценты, такие, чтобы минимизировать эмпирический риск , где — функция потерь.
Очевидно, что сложно найти сразу Основная идея в том, чтоб найти решение пошагово . Таким образом мы сможем постепенно оценивать изменение эмпирического риска .
Алгоритмы бустинга:
- AdaBoost — адаптивный алгоритм бустинга, усиливающий классификаторы, объединяя их в «комитет». Чувствителен к шуму.
- BrownBoost — алгоритм бустинга, эффективный на зашумленных наборах данных
- GradientBoost — алгоритм бустинга, использующий идеи линейной регресии
- LogitBoost — алгоритм бустинга, использующий идеи логистической регресси
Реализации и применения бустинга
Реализации бустинга:
- XGBoost — одна из самых популярных и эффективных реализаций алгоритма градиентного бустинга на деревьях на 2019-й год.
- CatBoost — открытая программная библиотека, разработанная компанией Яндекс.
- LightGBM — библиотека для метода машинного обучения, основанная на градиентном бустинге (англ. gradient boosting).
Применение бустинга:
- поисковые системы
- ранжирования ленты рекомендаций
- прогноз погоды
- оптимизации расхода сырья
- предсказания дефектов при производстве.
- исследованиях на Большом адронном коллайдере (БАК) для объединения информации с различных частей детектора LHCb в максимально точное, агрегированное знание о частице.
Различия между алгоритмами
- Оба алгоритма используют N базовых классификаторов
- Бустинг использует последовательное обучение
- Бэггинг использует параллельное обучение
- Оба генерируют несколько наборов данных для обучения путем случайной выборки
- Бустинг определяет вес данных, чтоб утяжелить тяжелые случаи
- Бэггинг имеет невзвешенные данные
- Оба принимают окончательное решение, усредняя N классификаторов
- В бустинге определяются веса для них
- В бэггинге они равнозначны
- Оба уменьшают дисперсию и обеспечивают более высокую стабильность
- Бэггинг может решить проблему переобучения
- Бустинг пытается уменьшить смещение, но может увеличить проблему переобучения
Примеры кода
Инициализация
from pydataset import data #Считаем данные The Boston Housing Dataset[1] df = data('Housing')
#Проверим данные
df.head().values
array([[42000.0, 5850, 3, 1, 2, 'yes', 'no', 'yes', 'no', 'no', 1, 'no'],
[38500.0, 4000, 2, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'],
[49500.0, 3060, 3, 1, 1, 'yes', 'no', 'no', 'no', 'no', 0, 'no'], ...
# Создадим словарь для слов 'no', 'yes'
d = dict(zip(['no', 'yes'], range(0,2)))
for i in zip(df.dtypes.index, df.dtypes):
if str(i[1]) == 'object':
df[i[0]] = df[i[0]].map(d)
df[‘price’] = pd.qcut(df[‘price’], 3, labels=[‘0’, ‘1’, ‘2’]).cat.codes
# Разделим множество на два
y = df['price']
X = df.drop('price', 1)
Бэггинг
# Импорты классификаторов
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier, ExtraTreesClassifier, RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import RidgeClassifier
from sklearn.svm import SVC
seed = 1075
np.random.seed(seed)
# Инициализуруем классификаторы
rf = RandomForestClassifier()
et = ExtraTreesClassifier()
knn = KNeighborsClassifier()
svc = SVC()
rg = RidgeClassifier()
clf_array = [rf, et, knn, svc, rg]
for clf in clf_array:
vanilla_scores = cross_val_score(clf, X, y, cv=10, n_jobs=-1)
bagging_clf = BaggingClassifier(clf, max_samples=0.4, max_features=10, random_state=seed)
bagging_scores = cross_val_score(bagging_clf, X, y, cv=10, n_jobs=-1)
print "Mean of: {1:.3f}, std: (+/-) {2:.3f [{0}]"
.format(clf.__class__.__name__,
vanilla_scores.mean(), vanilla_scores.std())
print "Mean of: {1:.3f}, std: (+/-) {2:.3f} [Bagging {0}]\n"
.format(clf.__class__.__name__,
bagging_scores.mean(), bagging_scores.std())
#Результат Mean of: 0.632, std: (+/-) 0.081 [RandomForestClassifier] Mean of: 0.639, std: (+/-) 0.069 [Bagging RandomForestClassifier] Mean of: 0.636, std: (+/-) 0.080 [ExtraTreesClassifier] Mean of: 0.654, std: (+/-) 0.073 [Bagging ExtraTreesClassifier] Mean of: 0.500, std: (+/-) 0.086 [KNeighborsClassifier] Mean of: 0.535, std: (+/-) 0.111 [Bagging KNeighborsClassifier] Mean of: 0.465, std: (+/-) 0.085 [SVC] Mean of: 0.535, std: (+/-) 0.083 [Bagging SVC] Mean of: 0.639, std: (+/-) 0.050 [RidgeClassifier] Mean of: 0.597, std: (+/-) 0.045 [Bagging RidgeClassifier]
Бустинг
ada_boost = AdaBoostClassifier()
grad_boost = GradientBoostingClassifier()
xgb_boost = XGBClassifier()
boost_array = [ada_boost, grad_boost, xgb_boost]
eclf = EnsembleVoteClassifier(clfs=[ada_boost, grad_boost, xgb_boost], voting='hard')
labels = ['Ada Boost', 'Grad Boost', 'XG Boost', 'Ensemble']
for clf, label in zip([ada_boost, grad_boost, xgb_boost, eclf], labels):
scores = cross_val_score(clf, X, y, cv=10, scoring='accuracy')
print("Mean: {0:.3f}, std: (+/-) {1:.3f} [{2}]".format(scores.mean(), scores.std(), label))
# Результат Mean: 0.641, std: (+/-) 0.082 [Ada Boost] Mean: 0.654, std: (+/-) 0.113 [Grad Boost] Mean: 0.663, std: (+/-) 0.101 [XG Boost] Mean: 0.667, std: (+/-) 0.105 [Ensemble]