Срез, согласованный срез — различия между версиями
Yeputons (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 2 участников) | |||
| Строка 3: | Строка 3: | ||
Пусть $E$ — множество событий с полным порядком ($<$) в рамках каждого процесса. | Пусть $E$ — множество событий с полным порядком ($<$) в рамках каждого процесса. | ||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Срез''' $F$ — подмножество $E$ такое, что если $e < f \in F$, то $e \in F. | + | '''Срез''' $F$ — подмножество $E$ такое, что если $e < f \in F$, то $e \in F$. |
| − | }} | + | }} |
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Согласованный срез''' $G$ — подмножество $E такое, что <tex>\forall f \in E, \forall g \in G : f \rightarrow g \Rightarrow f \in G</tex>. | + | '''Согласованный срез''' $G$ — подмножество $E$ такое, что <tex>\forall f \in E, \forall g \in G : f \rightarrow g \Rightarrow f \in G</tex>. |
}} | }} | ||
| − | |||
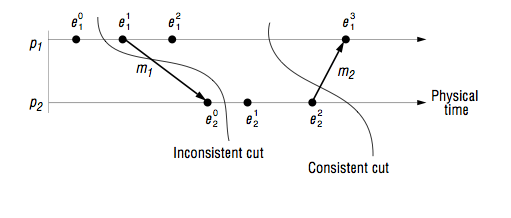
Это означает, что не существует сообщения переданного "через срез" в обратную сторону, т.е не бывает такого, что событие отправки сообщения не вошло в согласованный срез, а принятия вошло (см. рисунок <tex>m_1</tex> - несогласованный срез, <tex>m_2</tex> - согласованный срез). Можем говорить о том, что согласованный срез показывает некий глобальный снимок нашей системы. | Это означает, что не существует сообщения переданного "через срез" в обратную сторону, т.е не бывает такого, что событие отправки сообщения не вошло в согласованный срез, а принятия вошло (см. рисунок <tex>m_1</tex> - несогласованный срез, <tex>m_2</tex> - согласованный срез). Можем говорить о том, что согласованный срез показывает некий глобальный снимок нашей системы. | ||
| Строка 19: | Строка 16: | ||
Эквивалентное определение: не существует $f \in G, e \in E \setminus G$ таких, что $e \to f$. | Эквивалентное определение: не существует $f \in G, e \in E \setminus G$ таких, что $e \to f$. | ||
| + | |||
| + | Пусть $G$ и $H$ — согласованные срезы. Будем говорить, что $G \le H$, если H достижимо из G (т.е. $G \subseteq H$ в смысле событий). | ||
| + | |||
| + | == Теоремы == | ||
| + | === Нижняя граница для срезов === | ||
| + | Заметим, что если есть два согласованных среза $G_1$ и $G_2$, то срез $G_1 \cap G_2$ тоже согласован и, более того, $(G_1 \cap G_2) \le G_1, G_2$. | ||
| + | Доказательство: рассмотрим, какие сообщения могут пересылаться между различными частями системы: | ||
| + | {|border="1" style="text-align: center" | ||
| + | |откуда\куда | ||
| + | |$G_1 \cap G_2$ | ||
| + | |$G_1 \cap \bar G_2$ | ||
| + | |$\bar G_1 \cap G_2$ | ||
| + | |$\bar G_1 \cap \bar G_2$ | ||
| + | |- | ||
| + | |$G_1 \cap G_2$ || + || + || + || + | ||
| + | |- | ||
| + | |$G_1 \cap \bar G_2$ || - || + || - || + | ||
| + | |- | ||
| + | |$\bar G_1 \cap G_2$ || - || - || + || + | ||
| + | |- | ||
| + | |$\bar G_1 \cap \bar G_2$ || - || - || - || + | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Заметим, что не существует сообщений, которые бы пересылались из $E \setminus (G_1 \cap G_2)$ в $G_1 \cap G_2$, что и требовалось. | ||
| + | |||
| + | === Признак согласованности среза через векторные часы === | ||
| + | Если у нас есть срез $G$, в котором векторные часы последних отправленных сообщений всех процессов попарно несравнимы, то этот срез согласован. | ||
| + | Используется в алгоритме поиска слабого конъюнктивного предиката. | ||
| + | |||
| + | Доказательство от противного: пусть $G$ не согласован, тогда есть два события $f \in G$, $e \in E \setminus G$, причём $e \to f$. Тогда рассмотрим $e'$ — последнее событие $proc(e)$ в срезе $G$ (очевидно, $e' \le e$) и $f'$ — последнее событие $proc(f)$ в срезе $G$ (очевидно, что $f \le f'$). Тогда $e' \le e \to f \le f'$, т.е. $e' \to f'$, а тогда $VC(e') \le VC(f')$, противоречие. | ||
| + | |||
| + | Обратное, впрочем, неверно: можно рассмотреть ситуацию, в которой один поток отправил одно сообщение второму. Тогда у них векторные часы $(1, 0)$ и $(1, 1)$, они сравнимы, но срез согласованный. | ||
Текущая версия на 19:41, 4 сентября 2022
Мотивация: если у распределенной системы нет «глобального состояния», то как запомнить её состояние на диске, чтобы можно было продолжить работу после восстановления с диска?
Пусть $E$ — множество событий с полным порядком ($<$) в рамках каждого процесса.
| Определение: |
| Срез $F$ — подмножество $E$ такое, что если $e < f \in F$, то $e \in F$. |
| Определение: |
| Согласованный срез $G$ — подмножество $E$ такое, что . |
Это означает, что не существует сообщения переданного "через срез" в обратную сторону, т.е не бывает такого, что событие отправки сообщения не вошло в согласованный срез, а принятия вошло (см. рисунок - несогласованный срез, - согласованный срез). Можем говорить о том, что согласованный срез показывает некий глобальный снимок нашей системы.
Эквивалентное определение: не существует $f \in G, e \in E \setminus G$ таких, что $e \to f$.
Пусть $G$ и $H$ — согласованные срезы. Будем говорить, что $G \le H$, если H достижимо из G (т.е. $G \subseteq H$ в смысле событий).
Теоремы
Нижняя граница для срезов
Заметим, что если есть два согласованных среза $G_1$ и $G_2$, то срез $G_1 \cap G_2$ тоже согласован и, более того, $(G_1 \cap G_2) \le G_1, G_2$. Доказательство: рассмотрим, какие сообщения могут пересылаться между различными частями системы:
| откуда\куда | $G_1 \cap G_2$ | $G_1 \cap \bar G_2$ | $\bar G_1 \cap G_2$ | $\bar G_1 \cap \bar G_2$ |
| $G_1 \cap G_2$ | + | + | + | + |
| $G_1 \cap \bar G_2$ | - | + | - | + |
| $\bar G_1 \cap G_2$ | - | - | + | + |
| $\bar G_1 \cap \bar G_2$ | - | - | - | + |
Заметим, что не существует сообщений, которые бы пересылались из $E \setminus (G_1 \cap G_2)$ в $G_1 \cap G_2$, что и требовалось.
Признак согласованности среза через векторные часы
Если у нас есть срез $G$, в котором векторные часы последних отправленных сообщений всех процессов попарно несравнимы, то этот срез согласован. Используется в алгоритме поиска слабого конъюнктивного предиката.
Доказательство от противного: пусть $G$ не согласован, тогда есть два события $f \in G$, $e \in E \setminus G$, причём $e \to f$. Тогда рассмотрим $e'$ — последнее событие $proc(e)$ в срезе $G$ (очевидно, $e' \le e$) и $f'$ — последнее событие $proc(f)$ в срезе $G$ (очевидно, что $f \le f'$). Тогда $e' \le e \to f \le f'$, т.е. $e' \to f'$, а тогда $VC(e') \le VC(f')$, противоречие.
Обратное, впрочем, неверно: можно рассмотреть ситуацию, в которой один поток отправил одно сообщение второму. Тогда у них векторные часы $(1, 0)$ и $(1, 1)$, они сравнимы, но срез согласованный.