Алгоритмы сэмплирования — различия между версиями
(→Дополнительные) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 7 промежуточных версий 3 участников) | |||
| Строка 2: | Строка 2: | ||
Неравномерное распределение может быть следующих типов: | Неравномерное распределение может быть следующих типов: | ||
| − | * Недостаточное представление класса в независимой переменной; | + | * Недостаточное представление класса в ''независимой'' переменной; |
| − | * Недостаточное представление класса в зависимой переменной. | + | * Недостаточное представление класса в ''зависимой'' переменной. |
Многие модели машинного обучения, например, нейронные сети, дают более надежные прогнозы на основе обучения со сбалансированными данными. Однако некоторые аналитические методы, в частности [[Линейная_регрессия|линейная регрессия]] и [[Логистическая_регрессия|логистическая регрессия]], не получают дополнительного преимущества. | Многие модели машинного обучения, например, нейронные сети, дают более надежные прогнозы на основе обучения со сбалансированными данными. Однако некоторые аналитические методы, в частности [[Линейная_регрессия|линейная регрессия]] и [[Логистическая_регрессия|логистическая регрессия]], не получают дополнительного преимущества. | ||
| Строка 18: | Строка 18: | ||
Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные). | Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные). | ||
| + | |||
| + | * '''Случайное сэмплирование''' (англ. ''random sampling'') {{---}} для этого типа сэмплирования существует равная вероятность выбора любого конкретного элемента. Например, выбор 10 чисел в промежутке от 1 до 100. Здесь каждое число имеет равную вероятность быть выбранным. | ||
| + | ** '''Сэплирование с заменой''' (англ. ''sampling with replacement'') {{---}} здесь элемент, который выбирается первым, не должен влиять на вторую или любую другую выборку. Математически, ковариация равна нулю между двумя выборками. Мы должны использовать выборку с заменой, когда у нас большой набор данных. Потому что, если мы используем выборку без замены, то вероятность для каждого предмета, который будет выбран, будет изменяться, и она будет слишком сложной после определенного момента. Выборка с заменой может сказать нам, что чаще встречается в наших данных. | ||
| + | ** '''Сэмплирование без замены''' (англ. ''sampling without replacement'') {{---}} здесь то, что мы выбираем первым, повлияет на второе. Выборка без замены полезна, если набор данных мал. Математически, ковариация между двумя выборками не равна нулю. | ||
| + | * '''Стратифицированное сэмплирование''' (англ. ''stratified sampling'') {{---}} в этом типе техники мы выбираем из определенной группы объектов из всей выборки. Из каждой группы извлекается одинаковое количество объектов, хотя группы имеют разные размеры. Кроме того, существует вариант, когда количество объектов, выбранных из каждой группы, пропорционально размеру этой группы. | ||
| + | |||
| + | == Метод Uncertainty Sampling == | ||
| + | '''Идея:''' выбирать <math>x_i</math> с наибольшей неопределенностью <math>a(x_i)</math>. | ||
| + | |||
| + | Задача многоклассовой классификации: | ||
| + | |||
| + | <math>a(x)=\arg\max\limits_{y\in Y}P(y \mid x)</math> | ||
| + | |||
| + | <math>p_k(x), k=1\ldots\left | Y \right |</math> {{---}} ранжированные по убыванию <math>P(y \mid x), y\in Y</math>. | ||
| + | |||
| + | * Принцип наименьшей достоверности (англ. ''least confidence''): | ||
| + | :<math>x_i=\arg\min\limits_{u\in X^k}p_1(u)</math> | ||
| + | * Принцип наименьшей разности отступов (англ. ''margin sampling''): | ||
| + | :<math>x_i=\arg\min\limits_{u\in X^k}(p_1(u)-p_2(u))</math> | ||
| + | * Принцип максимума энтропии (англ. ''maximum entropy''): | ||
| + | :<math>x_i=\arg\min\limits_{x\in X^k}\sum_{k} {p_k(u)\ln p_k(u)}</math> | ||
| + | |||
| + | В случае двух классов эти три принципа эквивалентны. В случае многих классов появляются различия. | ||
== Примеры алгоритмов == | == Примеры алгоритмов == | ||
| Строка 54: | Строка 77: | ||
* NearMiss <math>(1 \And 2 \And 3)</math><ref>I. Mani, J. Zhang. “kNN approach to unbalanced data distributions: A case study involving information extraction,” In Proceedings of the Workshop on Learning from Imbalanced Data Sets, pp. 1-7, 2003.</ref> {{---}} удаляет примеры мажоритарного класса, для которых среднее расстояние до ближайших соседей ([[Метрический_классификатор_и_метод_ближайших_соседей|KNN]]) миноритарного класса является наименьшим. Также может использоваться расстояние до самых дальних соседей, либо среднее расстояние до всех соседей. | * NearMiss <math>(1 \And 2 \And 3)</math><ref>I. Mani, J. Zhang. “kNN approach to unbalanced data distributions: A case study involving information extraction,” In Proceedings of the Workshop on Learning from Imbalanced Data Sets, pp. 1-7, 2003.</ref> {{---}} удаляет примеры мажоритарного класса, для которых среднее расстояние до ближайших соседей ([[Метрический_классификатор_и_метод_ближайших_соседей|KNN]]) миноритарного класса является наименьшим. Также может использоваться расстояние до самых дальних соседей, либо среднее расстояние до всех соседей. | ||
* Edited Nearest Neighbours<ref>D. Wilson, “Asymptotic Properties of Nearest Neighbor Rules Using Edited Data,” IEEE Transactions on Systems, Man, and Cybernetrics, vol. 2(3), pp. 408-421, 1972.</ref> {{---}} удаляет примеры мажоритарного класса, если при классификации методом [[Метрический_классификатор_и_метод_ближайших_соседей|KNN]] они определяются как примеры миноритарного класса. | * Edited Nearest Neighbours<ref>D. Wilson, “Asymptotic Properties of Nearest Neighbor Rules Using Edited Data,” IEEE Transactions on Systems, Man, and Cybernetrics, vol. 2(3), pp. 408-421, 1972.</ref> {{---}} удаляет примеры мажоритарного класса, если при классификации методом [[Метрический_классификатор_и_метод_ближайших_соседей|KNN]] они определяются как примеры миноритарного класса. | ||
| − | |||
=== Передискретизации (увеличение числа примеров миноритарного класса) === | === Передискретизации (увеличение числа примеров миноритарного класса) === | ||
| Строка 63: | Строка 85: | ||
Этот алгоритм основан на идее генерации некоторого количества искусственных примеров, которые были бы похожи на имеющиеся в миноритарном классе, но при этом не дублировали их. Для создания новой записи находят разность <math>d=X_b–X_a</math>, где <math>X_a</math>,<math>X_b</math> – векторы признаков «соседних» примеров <math>a</math> и <math>b</math> из миноритарного класса. Их находят, используя алгоритм ближайшего соседа [[Метрический_классификатор_и_метод_ближайших_соседей|KNN]]. В данном случае необходимо и достаточно для примера <math>b</math> получить набор из <math>k</math> соседей, из которого в дальнейшем будет выбрана запись <math>b</math>. Остальные шаги алгоритма ''KNN'' не требуются. | Этот алгоритм основан на идее генерации некоторого количества искусственных примеров, которые были бы похожи на имеющиеся в миноритарном классе, но при этом не дублировали их. Для создания новой записи находят разность <math>d=X_b–X_a</math>, где <math>X_a</math>,<math>X_b</math> – векторы признаков «соседних» примеров <math>a</math> и <math>b</math> из миноритарного класса. Их находят, используя алгоритм ближайшего соседа [[Метрический_классификатор_и_метод_ближайших_соседей|KNN]]. В данном случае необходимо и достаточно для примера <math>b</math> получить набор из <math>k</math> соседей, из которого в дальнейшем будет выбрана запись <math>b</math>. Остальные шаги алгоритма ''KNN'' не требуются. | ||
Далее из <math>d</math> путем умножения каждого его элемента на случайное число в интервале <math>(0, 1)</math> получают <math>\hat{d}</math>. Вектор признаков нового примера вычисляется путем сложения <math>X_a</math> и <math>\hat{d}</math>. Алгоритм ''SMOTE'' позволяет задавать количество записей, которое необходимо искусственно сгенерировать. Степень сходства примеров <math>a</math> и <math>b</math> можно регулировать путем изменения числа ближайших соседей <math>k</math>. На рис. <math>4</math> схематично изображено то, как в двумерном пространстве признаков могут располагаться искусственно сгенерированные примеры. | Далее из <math>d</math> путем умножения каждого его элемента на случайное число в интервале <math>(0, 1)</math> получают <math>\hat{d}</math>. Вектор признаков нового примера вычисляется путем сложения <math>X_a</math> и <math>\hat{d}</math>. Алгоритм ''SMOTE'' позволяет задавать количество записей, которое необходимо искусственно сгенерировать. Степень сходства примеров <math>a</math> и <math>b</math> можно регулировать путем изменения числа ближайших соседей <math>k</math>. На рис. <math>4</math> схематично изображено то, как в двумерном пространстве признаков могут располагаться искусственно сгенерированные примеры. | ||
| + | |||
| + | В SMOTE (техника избыточной выборки синтетического меньшинства) мы синтезируем элементы для класса меньшинства в непосредственной близости от уже существующих элементов.<br /><code>from imblearn.over_sampling import SMOTE<br />smote = SMOTE(ratio='minority')<br />X_sm, y_sm = smote.fit_sample(X, y)</code><br />В библиотеке ''imblearn'' есть множество других методов как для недостаточной выборки (Cluster Centroids, NearMiss и т.д.), так и для избыточной выборки (ADASYN и bSMOTE). | ||
[[Файл:Smote_overgeneralization.png|thumb|right|upright=1.2|Рис. <math>5</math>. Негативное влияние алгоритма SMOTE]] | [[Файл:Smote_overgeneralization.png|thumb|right|upright=1.2|Рис. <math>5</math>. Негативное влияние алгоритма SMOTE]] | ||
==== '''ASMO''' (англ. ''Adaptive Synthetic Minority Oversampling'') ==== | ==== '''ASMO''' (англ. ''Adaptive Synthetic Minority Oversampling'') ==== | ||
| Строка 73: | Строка 97: | ||
Такая модификация алгоритма ''SMOTE'' делает его более адаптивным к различным наборам данных с несбалансированными классами. Общее представление идеи алгоритма показано на рис. <math>6</math>. | Такая модификация алгоритма ''SMOTE'' делает его более адаптивным к различным наборам данных с несбалансированными классами. Общее представление идеи алгоритма показано на рис. <math>6</math>. | ||
==== Дополнительные ==== | ==== Дополнительные ==== | ||
| − | * SMOTENC | + | * SMOTENC<ref>N. V. Chawla, K. W. Bowyer, L. O. Hall, W. P. Kegelmeyer, “SMOTE: Synthetic minority over-sampling technique,” Journal of Artificial Intelligence Research, vol. 16, pp. 321-357, 2002.</ref> {{---}} в отличие от ''SMOTE'', работает с непрерывными признаками у примеров обучающей выборки. |
* Borderline-SMOTE <math>(1 \And 2)</math><ref>H. Han, W.-Y. Wang, B.-H. Mao, “Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning,” In Proceedings of the 1st International Conference on Intelligent Computing, pp. 878-887, 2005.</ref> {{---}} в отличие от ''SMOTE'', для создания новых синтетических примеров используются только примеры на границе классов. | * Borderline-SMOTE <math>(1 \And 2)</math><ref>H. Han, W.-Y. Wang, B.-H. Mao, “Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning,” In Proceedings of the 1st International Conference on Intelligent Computing, pp. 878-887, 2005.</ref> {{---}} в отличие от ''SMOTE'', для создания новых синтетических примеров используются только примеры на границе классов. | ||
* SVM SMOTE - Support Vectors SMOTE<ref>H. M. Nguyen, E. W. Cooper, K. Kamei, “Borderline over-sampling for imbalanced data classification,” In Proceedings of the 5th International Workshop on computational Intelligence and Applications, pp. 24-29, 2009.</ref> {{---}} вариант алгоритма ''SMOTE'', который использует алгоритм [[Метод_опорных_векторов_(SVM)|SVM]] для обнаружения примеров, рядом с которыми будут создаваться новые синтетические примеры. | * SVM SMOTE - Support Vectors SMOTE<ref>H. M. Nguyen, E. W. Cooper, K. Kamei, “Borderline over-sampling for imbalanced data classification,” In Proceedings of the 5th International Workshop on computational Intelligence and Applications, pp. 24-29, 2009.</ref> {{---}} вариант алгоритма ''SMOTE'', который использует алгоритм [[Метод_опорных_векторов_(SVM)|SVM]] для обнаружения примеров, рядом с которыми будут создаваться новые синтетические примеры. | ||
| + | |||
| + | === '''Алгоритм Метрополиса — Гастингса''' === | ||
| + | Алгоритм позволяет семплировать любую функцию распределения. Он основан на создании цепи Маркова, то есть на каждом шаге алгоритма новое выбранное значение зависит только от предыдущего. | ||
| + | * Очередная итерация начинается с состояния <math>x^{(i)}</math> | ||
| + | * Выбираем <math>x^{\prime}</math> по распределению <math>q(x^\prime; x^{(i)})</math> | ||
| + | * Вычисляем: | ||
| + | :<math>a(x^{\prime}, x)=\frac{p^{*}(x^{\prime})}{p^{*}(x^{(i)})} \frac{q(x^{(i)}; x^{\prime})}{q(x^{\prime}; x^{(i)})}</math> | ||
| + | * С вероятностью <math>a(x^{\prime}, x)</math> (<math>1</math>, если <math>a\geq 1</math>) <math>x^{(i+1)}:=x^{\prime}</math>, иначе <math>x^{(i+1)}:=x^{(i)}</math> | ||
| + | |||
| + | === '''Сэмплирование по Гиббсу''' === | ||
| + | Этот алгоритм является частным случаем алгоритма Метрополиса — Гастингса и назван в честь физика Джозайи Гиббса. Он замечателен тем, что для него не требуется явно выраженное совместное распределение, а нужны лишь условные вероятности для каждой переменной, входящей в распределение. Алгоритм на каждом шаге берет одну случайную величину и выбирает её значение при условии фиксированных остальных.<br/><math>x_{i}^{t+1}</math> выбираем по распределению <math>p(x_{i}\mid x_{1}^{t+1},\ldots,x_{i-1}^{t+1},x_{i+1}^{t},\ldots,x_{n}^{t})</math> и повторяем.<br/>Это частный случай алгоритма Метрополиса для распределений <math>q(x^{\prime}; x)=p(x_{i}^{\prime}\mid x_{-i})</math>, и вероятность принятия каждого сэмпла полается равна <math>1</math>. Поэтому сэмплирование по Гиббсу сходится, и, так как это такое же случайное блуждание по сути, верна та же квадратичная оценка. В больших размерностях может оказаться эффективнее сэмплить по несколько переменных сразу, а не по одной — например, часто бывает, что у нас двудольный граф из переменных, в которых все переменные из одной доли связаны со всеми переменными из другой доли (ну или со многими), а между собой не связаны. В такой ситуации следует зафиксировать все переменные одной доли и просэмплировать все переменные в другой доле одновременно (это можно понимать буквально — поскольку при такой структуре все переменные одной доли условно независимы при условии другой, их можно сэмплировать независимо и параллельно), потом зафиксировать все переменные второй доли и так далее. | ||
| + | |||
| + | === '''Slice sampling''' === | ||
| + | Выборка среза представляет собой тип алгоритма Монте Карло по схеме марковских цепей для выборки псевдослучайных чисел, т.е. для отбора случайных выборок из статистического распределения. Метод основан на наблюдении, что для выборки случайной величины можно равномерно выбирать из области под графиком ее функции плотности. | ||
| + | |||
| + | Slice sampling, в его самой простой форме, равномерно выбирается из-под кривой <math>f(x)</math> без необходимости отбрасывать какие-либо точки следующими действиями: | ||
| + | * Выберите начальное значение <math>x_{0}</math>, для которого <math>f(x_{0})>0</math> | ||
| + | * Выберите значение <math>y</math> равномерно между <math>0</math> и <math>f(x_{0})</math> | ||
| + | * Проведите горизонтальную линию через кривую в этой координате <math>y</math> | ||
| + | * Выберите точку <math>(x, y)</math> на отрезке в пределах кривой | ||
| + | * Повторите с шага <math>2</math>, используя новое значение <math>x</math> | ||
| + | |||
| + | Суть здесь заключается в том, что один из способов равномерной выборки точки из произвольной кривой — это сначала нарисовать тонкие горизонтальные срезы одинаковой высоты по всей кривой. Затем мы можем сэмплировать точку внутри кривой путем случайного выбора среза, который находится в точке или ниже кривой в позиции <math>x</math> на предыдущей итерации, а затем случайным образом выбрать позицию <math>x</math> где-нибудь вдоль среза. Используя позицию <math>x</math> из предыдущей итерации алгоритма, в долгосрочной перспективе мы выбираем срезы с вероятностями, пропорциональными длине их сегментов в пределах кривой. Самая сложная часть этого алгоритма — это поиск границ горизонтального среза, который включает в себя инвертирование функции, описывающей распределение, из которого производится выборка. Это особенно проблематично для мультимодальных распределений, где срез может состоять из нескольких прерывистых частей. Часто можно использовать форму выборки отклонения, чтобы преодолеть это, когда мы производим выборку из более крупного среза, который, как известно, включает в себя требуемый рассматриваемый срез, а затем отбрасываем точки за пределами желаемого среза. Этот алгоритм можно использовать для выборки из области под любой кривой, независимо от того, интегрируется ли функция в <math>1</math>. Фактически, масштабирование функции по константе не влияет на выборочные <math>x</math>—позиции. Это означает, что алгоритм может использоваться для выборки из распределения, функция плотности вероятности которого известна только с точностью до константы. | ||
=== Комбинирование === | === Комбинирование === | ||
| − | * SMOTE <math>+</math> Tomek links<ref> | + | * SMOTE <math>+</math> Tomek links<ref>G. E. A. P. A. Batista, A. L. C. Bazzan, M. C. Monard, “Balancing training data for automated annotation of keywords: A case study,” In Proceedings of the 2nd Brazilian Workshop on Bioinformatics, pp. 10-18, 2003.</ref> {{---}} сначала выполняет передискретизацию с использованием ''SMOTE'', а потом субдискретизацию используя ''Tomek Links''. |
| − | * SMOTE <math>+</math> ENN<ref> | + | * SMOTE <math>+</math> ENN<ref>G. E. A. P. A. Batista, R. C. Prati, M. C. Monard, “A study of the behavior of several methods for balancing machine learning training data,” ACM Sigkdd Explorations Newsletter, vol. 6(1), pp. 20-29, 2004.</ref> {{---}} последовательно использует ''SMOTE'' и ''Edited Nearest Neighbours''. |
=== Ансамбль сбалансированных наборов === | === Ансамбль сбалансированных наборов === | ||
| − | * Easy Ensemble classifier<ref> | + | * Easy Ensemble classifier<ref>X.-Y. Liu, J. Wu and Z.-H. Zhou, “Exploratory undersampling for class-imbalance learning,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 39(2), pp. 539-550, 2009.</ref> {{---}} независимые классификаторы обучаются на случайных подвыборках, из которых постепенно удаляются правильно классифицирующиеся примеры мажоритарных классов. |
| − | * Balanced Random Forest<ref> | + | * Balanced Random Forest<ref>C. Chao, A. Liaw, and L. Breiman. "Using random forest to learn imbalanced data." University of California, Berkeley 110 (2004): 1-12.</ref> {{---}} в отличие от классического [[Дерево_решений_и_случайный_лес|случайного леса]], может работать на несбалансированных данных. |
| − | * Balanced Bagging<ref> | + | * Balanced Bagging<ref>Hido, Shohei & Kashima, Hisashi. (2008). Roughly Balanced Bagging for Imbalanced Data. 143-152. 10.1137/1.9781611972788.13. </ref> {{---}} в отличие от классического [[Виды_ансамблей#.D0.91.D1.8D.D0.B3.D0.B3.D0.B8.D0.BD.D0.B3|бэггинга]], имеет дополнительный шаг субдискретизации обучающей подвыборки. |
| − | |||
== Реализации == | == Реализации == | ||
Текущая версия на 19:16, 4 сентября 2022
Сэмплирование (англ. data sampling) — метод корректировки обучающей выборки с целью балансировки распределения классов в исходном наборе данных. Нужно отличать этот метод от сэмплирования в активном обучении для отбора кандидатов и от сэмплирования в статистике[1] для создания подвыборки с сохранением распределения классов.
Неравномерное распределение может быть следующих типов:
- Недостаточное представление класса в независимой переменной;
- Недостаточное представление класса в зависимой переменной.
Многие модели машинного обучения, например, нейронные сети, дают более надежные прогнозы на основе обучения со сбалансированными данными. Однако некоторые аналитические методы, в частности линейная регрессия и логистическая регрессия, не получают дополнительного преимущества.
Когда в обучающем наборе данных доля примеров некоторого класса слишком мала, такие классы называются миноритарными (англ. minority), другие, со слишком большим количеством представителей, — мажоритарными (англ. majority). Подобные тенденции хорошо заметны в кредитном скоринге, в медицине, в директ-маркетинге.
Следует отметить то, что значимость ошибочной классификации может быть разной. Неверная классификация примеров миноритарного класса, как правило, обходится в разы дороже, чем ошибочная классификация примеров мажоритарного класса. Например, при классификации людей, обследованных в больнице, на больных раком (миноритарный класс) и здоровых (мажоритарный класс) лучше будет отправить на дополнительное обследование здоровых пациентов, чем пропустить людей с раком.
Содержание
- 1 Стратегии сэмплирования
- 2 Метод Uncertainty Sampling
- 3 Примеры алгоритмов
- 3.1 Cубдискретизация (удаление примеров мажоритарного класса)
- 3.1.1 Случайное удаление примеров мажоритарного класса (англ. Random Undersampling)
- 3.1.2 Поиск связей Томека (англ. Tomek Links)
- 3.1.3 Правило сосредоточенного ближайшего соседа (англ. Condensed Nearest Neighbor Rule)
- 3.1.4 Односторонний сэмплинг (англ. One-side sampling, one-sided selection)
- 3.1.5 Правило «очищающего» соседа (англ. Neighborhood cleaning rule)
- 3.1.6 Дополнительные
- 3.2 Передискретизации (увеличение числа примеров миноритарного класса)
- 3.3 Алгоритм Метрополиса — Гастингса
- 3.4 Сэмплирование по Гиббсу
- 3.5 Slice sampling
- 3.6 Комбинирование
- 3.7 Ансамбль сбалансированных наборов
- 3.1 Cубдискретизация (удаление примеров мажоритарного класса)
- 4 Реализации
- 5 См. также
- 6 Примечания
- 7 Источники информации
Стратегии сэмплирования
- Cубдискретизация (англ. under-sampling) — удаление некоторого количества примеров мажоритарного класса.
- Передискретизации (англ. over-sampling) — увеличение количества примеров миноритарного класса.
- Комбинирование (англ. сombining over- and under-sampling) — последовательное применение субдискретизации и передискретизации.
- Ансамбль сбалансированных наборов (англ. ensemble balanced sets) — использование встроенных методов сэмплирования в процессе построения ансамблей классификаторов.
Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные).
- Случайное сэмплирование (англ. random sampling) — для этого типа сэмплирования существует равная вероятность выбора любого конкретного элемента. Например, выбор 10 чисел в промежутке от 1 до 100. Здесь каждое число имеет равную вероятность быть выбранным.
- Сэплирование с заменой (англ. sampling with replacement) — здесь элемент, который выбирается первым, не должен влиять на вторую или любую другую выборку. Математически, ковариация равна нулю между двумя выборками. Мы должны использовать выборку с заменой, когда у нас большой набор данных. Потому что, если мы используем выборку без замены, то вероятность для каждого предмета, который будет выбран, будет изменяться, и она будет слишком сложной после определенного момента. Выборка с заменой может сказать нам, что чаще встречается в наших данных.
- Сэмплирование без замены (англ. sampling without replacement) — здесь то, что мы выбираем первым, повлияет на второе. Выборка без замены полезна, если набор данных мал. Математически, ковариация между двумя выборками не равна нулю.
- Стратифицированное сэмплирование (англ. stratified sampling) — в этом типе техники мы выбираем из определенной группы объектов из всей выборки. Из каждой группы извлекается одинаковое количество объектов, хотя группы имеют разные размеры. Кроме того, существует вариант, когда количество объектов, выбранных из каждой группы, пропорционально размеру этой группы.
Метод Uncertainty Sampling
Идея: выбирать с наибольшей неопределенностью .
Задача многоклассовой классификации:
— ранжированные по убыванию .
- Принцип наименьшей достоверности (англ. least confidence):
- Принцип наименьшей разности отступов (англ. margin sampling):
- Принцип максимума энтропии (англ. maximum entropy):
В случае двух классов эти три принципа эквивалентны. В случае многих классов появляются различия.
Примеры алгоритмов
Cубдискретизация (удаление примеров мажоритарного класса)
Случайное удаление примеров мажоритарного класса (англ. Random Undersampling)
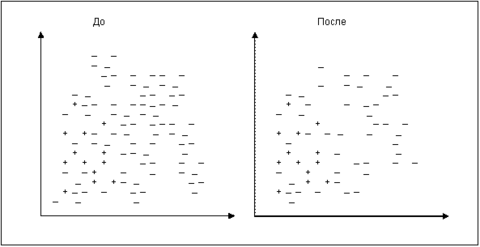
Это самый простой алгоритм. Рассчитывается число – количество мажоритарных примеров, которое необходимо удалить для достижения требуемого уровня соотношения различных классов. Затем случайным образом выбираются K мажоритарных примеров и удаляются. На рис. изображены примеры некоторого набора данных в двумерном пространстве признаков до и после использования алгоритма.
Поиск связей Томека (англ. Tomek Links)
Пусть примеры и принадлежат к различным классам, – расстояние между указанными примерами. Пара называется связью Томека, если не найдется ни одного примера такого, что будет справедлива совокупность неравенств:
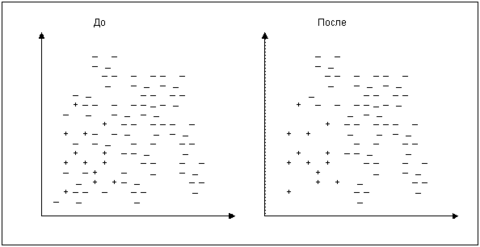
Согласно данному подходу, все мажоритарные записи, входящие в связи Томека, должны быть удалены из набора данных. Этот способ хорошо удаляет записи, которые можно рассматривать в качестве «зашумляющих». На рис. визуально показан набор данных в двумерном пространстве признаков до и после применения стратегии поиска связей Томека.
Правило сосредоточенного ближайшего соседа (англ. Condensed Nearest Neighbor Rule)
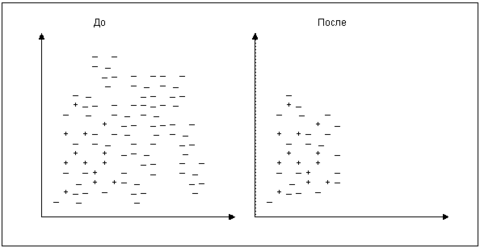
Пусть – исходный набор данных. Из него выбираются все миноритарные примеры и (случайным образом) один мажоритарный. Обозначим это множество как . Все примеры из классифицируются по правилу одного ближайшего соседа. Записи, получившие ошибочную метку, добавляются во множество (рис. ). Таким образом, мы будем учить классификатор находить отличие между похожими примерами, но принадлежащими к разным классам.
Односторонний сэмплинг (англ. One-side sampling, one-sided selection)
Главная идея этой стратегии – это последовательное сочетание предыдущих двух, рассмотренных выше. Для этого на первом шаге применяется правило сосредоточенного ближайшего соседа, а на втором – удаляются все мажоритарные примеры, участвующие в связях Томека. Таким образом, удаляются большие «сгустки» мажоритарных примеров, а затем область пространства со скоплением миноритарных очищается от потенциального шума.
Правило «очищающего» соседа (англ. Neighborhood cleaning rule)
Эта стратегия также направлена на то, чтобы удалить те примеры, которые негативно влияют на исход классификации миноритарных классов. Для этого все примеры классифицируются по правилу трех ближайших соседей. Удаляются следующие мажоритарные примеры:
- получившие верную метку класса;
- являющиеся соседями миноритарных примеров, которые были неверно классифицированы.
Дополнительные
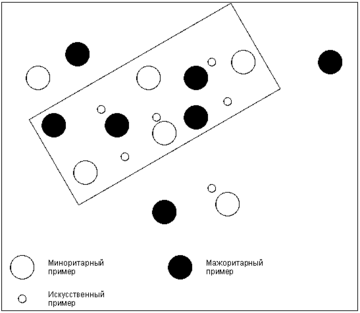
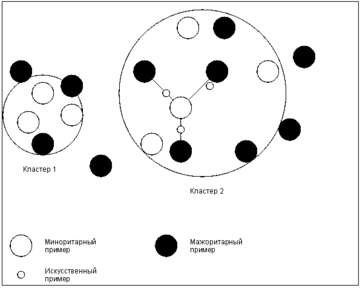
- Under-sampling with Cluster Centroids[2] — уменьшает количество примеров мажоритарного класса, заменяя некоторые кластеры примеров мажоритарного класса их представителем (центроидом кластера).
- NearMiss [3] — удаляет примеры мажоритарного класса, для которых среднее расстояние до ближайших соседей (KNN) миноритарного класса является наименьшим. Также может использоваться расстояние до самых дальних соседей, либо среднее расстояние до всех соседей.
- Edited Nearest Neighbours[4] — удаляет примеры мажоритарного класса, если при классификации методом KNN они определяются как примеры миноритарного класса.
Передискретизации (увеличение числа примеров миноритарного класса)
Дублирование примеров миноритарного класса (англ. Oversampling)
Самый простой метод – это дублирование примеров миноритарного класса. В зависимости от того, какое соотношение классов необходимо, выбирается количество случайных записей для дублирования.
SMOTE (англ. Synthetic Minority Oversampling Technique)
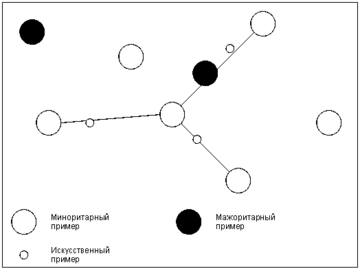
Этот алгоритм основан на идее генерации некоторого количества искусственных примеров, которые были бы похожи на имеющиеся в миноритарном классе, но при этом не дублировали их. Для создания новой записи находят разность , где , – векторы признаков «соседних» примеров и из миноритарного класса. Их находят, используя алгоритм ближайшего соседа KNN. В данном случае необходимо и достаточно для примера получить набор из соседей, из которого в дальнейшем будет выбрана запись . Остальные шаги алгоритма KNN не требуются. Далее из путем умножения каждого его элемента на случайное число в интервале получают . Вектор признаков нового примера вычисляется путем сложения и . Алгоритм SMOTE позволяет задавать количество записей, которое необходимо искусственно сгенерировать. Степень сходства примеров и можно регулировать путем изменения числа ближайших соседей . На рис. схематично изображено то, как в двумерном пространстве признаков могут располагаться искусственно сгенерированные примеры.
В SMOTE (техника избыточной выборки синтетического меньшинства) мы синтезируем элементы для класса меньшинства в непосредственной близости от уже существующих элементов.from imblearn.over_sampling import SMOTE
smote = SMOTE(ratio='minority')
X_sm, y_sm = smote.fit_sample(X, y)
В библиотеке imblearn есть множество других методов как для недостаточной выборки (Cluster Centroids, NearMiss и т.д.), так и для избыточной выборки (ADASYN и bSMOTE).
ASMO (англ. Adaptive Synthetic Minority Oversampling)
Алгоритм SMOTE имеет недостаток в том, что «вслепую» увеличивает плотность примерами в области слабо представленного класса (рис. ). В случае, если миноритарные примеры равномерно распределены среди мажоритарных и имеют низкую плотность, алгоритм SMOTE только сильнее перемешает классы. В качестве решения данной проблемы был предложен алгоритм адаптивного искусственного увеличения числа примеров миноритарного класса ASMO:
- Если для каждого -ого примера миноритарного класса из ближайших соседей принадлежит к мажоритарному, то набор данных считается «рассеянным». В этом случае используют алгоритм ASMO, иначе применяют SMOTE (как правило, задают равным ).
- Используя только примеры миноритарного класса, выделить несколько кластеров (например, алгоритмом -средних).
- Сгенерировать искусственные записи в пределах отдельных кластеров на основе всех классов. Для каждого примера миноритарного класса находят ближайших соседей, и на основе них (также как в SMOTE) создаются новые записи.
Такая модификация алгоритма SMOTE делает его более адаптивным к различным наборам данных с несбалансированными классами. Общее представление идеи алгоритма показано на рис. .
Дополнительные
- SMOTENC[5] — в отличие от SMOTE, работает с непрерывными признаками у примеров обучающей выборки.
- Borderline-SMOTE [6] — в отличие от SMOTE, для создания новых синтетических примеров используются только примеры на границе классов.
- SVM SMOTE - Support Vectors SMOTE[7] — вариант алгоритма SMOTE, который использует алгоритм SVM для обнаружения примеров, рядом с которыми будут создаваться новые синтетические примеры.
Алгоритм Метрополиса — Гастингса
Алгоритм позволяет семплировать любую функцию распределения. Он основан на создании цепи Маркова, то есть на каждом шаге алгоритма новое выбранное значение зависит только от предыдущего.
- Очередная итерация начинается с состояния
- Выбираем по распределению
- Вычисляем:
- С вероятностью (, если ) , иначе
Сэмплирование по Гиббсу
Этот алгоритм является частным случаем алгоритма Метрополиса — Гастингса и назван в честь физика Джозайи Гиббса. Он замечателен тем, что для него не требуется явно выраженное совместное распределение, а нужны лишь условные вероятности для каждой переменной, входящей в распределение. Алгоритм на каждом шаге берет одну случайную величину и выбирает её значение при условии фиксированных остальных.
выбираем по распределению и повторяем.
Это частный случай алгоритма Метрополиса для распределений , и вероятность принятия каждого сэмпла полается равна . Поэтому сэмплирование по Гиббсу сходится, и, так как это такое же случайное блуждание по сути, верна та же квадратичная оценка. В больших размерностях может оказаться эффективнее сэмплить по несколько переменных сразу, а не по одной — например, часто бывает, что у нас двудольный граф из переменных, в которых все переменные из одной доли связаны со всеми переменными из другой доли (ну или со многими), а между собой не связаны. В такой ситуации следует зафиксировать все переменные одной доли и просэмплировать все переменные в другой доле одновременно (это можно понимать буквально — поскольку при такой структуре все переменные одной доли условно независимы при условии другой, их можно сэмплировать независимо и параллельно), потом зафиксировать все переменные второй доли и так далее.
Slice sampling
Выборка среза представляет собой тип алгоритма Монте Карло по схеме марковских цепей для выборки псевдослучайных чисел, т.е. для отбора случайных выборок из статистического распределения. Метод основан на наблюдении, что для выборки случайной величины можно равномерно выбирать из области под графиком ее функции плотности.
Slice sampling, в его самой простой форме, равномерно выбирается из-под кривой без необходимости отбрасывать какие-либо точки следующими действиями:
- Выберите начальное значение , для которого
- Выберите значение равномерно между и
- Проведите горизонтальную линию через кривую в этой координате
- Выберите точку на отрезке в пределах кривой
- Повторите с шага , используя новое значение
Суть здесь заключается в том, что один из способов равномерной выборки точки из произвольной кривой — это сначала нарисовать тонкие горизонтальные срезы одинаковой высоты по всей кривой. Затем мы можем сэмплировать точку внутри кривой путем случайного выбора среза, который находится в точке или ниже кривой в позиции на предыдущей итерации, а затем случайным образом выбрать позицию где-нибудь вдоль среза. Используя позицию из предыдущей итерации алгоритма, в долгосрочной перспективе мы выбираем срезы с вероятностями, пропорциональными длине их сегментов в пределах кривой. Самая сложная часть этого алгоритма — это поиск границ горизонтального среза, который включает в себя инвертирование функции, описывающей распределение, из которого производится выборка. Это особенно проблематично для мультимодальных распределений, где срез может состоять из нескольких прерывистых частей. Часто можно использовать форму выборки отклонения, чтобы преодолеть это, когда мы производим выборку из более крупного среза, который, как известно, включает в себя требуемый рассматриваемый срез, а затем отбрасываем точки за пределами желаемого среза. Этот алгоритм можно использовать для выборки из области под любой кривой, независимо от того, интегрируется ли функция в . Фактически, масштабирование функции по константе не влияет на выборочные —позиции. Это означает, что алгоритм может использоваться для выборки из распределения, функция плотности вероятности которого известна только с точностью до константы.
Комбинирование
- SMOTE Tomek links[8] — сначала выполняет передискретизацию с использованием SMOTE, а потом субдискретизацию используя Tomek Links.
- SMOTE ENN[9] — последовательно использует SMOTE и Edited Nearest Neighbours.
Ансамбль сбалансированных наборов
- Easy Ensemble classifier[10] — независимые классификаторы обучаются на случайных подвыборках, из которых постепенно удаляются правильно классифицирующиеся примеры мажоритарных классов.
- Balanced Random Forest[11] — в отличие от классического случайного леса, может работать на несбалансированных данных.
- Balanced Bagging[12] — в отличие от классического бэггинга, имеет дополнительный шаг субдискретизации обучающей подвыборки.
Реализации
Imbalanced-learn — набор инструментов с открытым исходным кодом на Python, целью которого является предоставление широкого спектра методов для решения проблемы несбалансированного набора данных. На рис. представлена таблица реализованных в библиотеке методов.
Пример кода для передискретизации набора данных с использованием SMOTE:
from sklearn.datasets import make_classification
from sklearn.decomposition import PCA
from imblearn.oversampling import SMOTE
# Создание датасета
X, y = makeclassification (n_classes=2, weights =[0.1, 0.9],
n_features=20, n_samples=5000)
Применение SMOTE over-sampling
sm = SMOTE(ratio=’auto’, kind=’regular’)
X_resampled , y_resampled=sm.fit_sample(X, y)
См. также
- Метрический классификатор и метод ближайших соседей
- Байесовская классификация
- Активное обучение
- Виды ансамблей
Примечания
- ↑ Sampling (statistics)
- ↑ Show-Jane Yen, Yue-Shi Lee,Cluster-based under-sampling approaches for imbalanced data distributions, Expert Systems with Applications, Volume 36, Issue 3, Part 1, 2009, Pages 5718-5727, ISSN 0957-4174
- ↑ I. Mani, J. Zhang. “kNN approach to unbalanced data distributions: A case study involving information extraction,” In Proceedings of the Workshop on Learning from Imbalanced Data Sets, pp. 1-7, 2003.
- ↑ D. Wilson, “Asymptotic Properties of Nearest Neighbor Rules Using Edited Data,” IEEE Transactions on Systems, Man, and Cybernetrics, vol. 2(3), pp. 408-421, 1972.
- ↑ N. V. Chawla, K. W. Bowyer, L. O. Hall, W. P. Kegelmeyer, “SMOTE: Synthetic minority over-sampling technique,” Journal of Artificial Intelligence Research, vol. 16, pp. 321-357, 2002.
- ↑ H. Han, W.-Y. Wang, B.-H. Mao, “Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning,” In Proceedings of the 1st International Conference on Intelligent Computing, pp. 878-887, 2005.
- ↑ H. M. Nguyen, E. W. Cooper, K. Kamei, “Borderline over-sampling for imbalanced data classification,” In Proceedings of the 5th International Workshop on computational Intelligence and Applications, pp. 24-29, 2009.
- ↑ G. E. A. P. A. Batista, A. L. C. Bazzan, M. C. Monard, “Balancing training data for automated annotation of keywords: A case study,” In Proceedings of the 2nd Brazilian Workshop on Bioinformatics, pp. 10-18, 2003.
- ↑ G. E. A. P. A. Batista, R. C. Prati, M. C. Monard, “A study of the behavior of several methods for balancing machine learning training data,” ACM Sigkdd Explorations Newsletter, vol. 6(1), pp. 20-29, 2004.
- ↑ X.-Y. Liu, J. Wu and Z.-H. Zhou, “Exploratory undersampling for class-imbalance learning,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 39(2), pp. 539-550, 2009.
- ↑ C. Chao, A. Liaw, and L. Breiman. "Using random forest to learn imbalanced data." University of California, Berkeley 110 (2004): 1-12.
- ↑ Hido, Shohei & Kashima, Hisashi. (2008). Roughly Balanced Bagging for Imbalanced Data. 143-152. 10.1137/1.9781611972788.13.
Источники информации
- Oversampling and undersampling in data analysis
- Различные стратегии сэмплинга в условиях несбалансированности классов
- Lemaître, G. Nogueira, F. Aridas, Ch.K. (2017) Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning, Journal of Machine Learning Research, vol. 18, no. 17, 2017, pp. 1-5.