Задача нахождения объектов на изображении — различия между версиями
(→Источники информации) (Метки: правка с мобильного устройства, правка из мобильной версии) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 5 промежуточных версий 4 участников) | |||
| Строка 17: | Строка 17: | ||
В задачах классификации с локализацией и детекции объектов для определения достоверности местоположения ограничивающей рамки в качестве метрики чаще всего используется отношение площадей ограничивающих рамок (англ. '''Intersection over Union'''): | В задачах классификации с локализацией и детекции объектов для определения достоверности местоположения ограничивающей рамки в качестве метрики чаще всего используется отношение площадей ограничивающих рамок (англ. '''Intersection over Union'''): | ||
| − | $IoU = \frac{S(A \ | + | $IoU = \frac{S(A \cap B)}{S(A \cup B)}$, |
где $A$ и $B$ {{---}} предсказанная ограничивающая рамка и настоящиая ограничивающая рамка соответственно. $IoU$ равно нулю в случае непересекающихся ограничивающих рамок и равно единице в случае идеального наложения. | где $A$ и $B$ {{---}} предсказанная ограничивающая рамка и настоящиая ограничивающая рамка соответственно. $IoU$ равно нулю в случае непересекающихся ограничивающих рамок и равно единице в случае идеального наложения. | ||
| Строка 126: | Строка 126: | ||
где $x$ {{---}} настоящая ограничивающая рамка, $c_i$ {{---}} центроид кластера. Количество ограничивающих рамок-центроидов выбирается при помощи "метода локтя" (англ. elbow method). Также в YOLOv2 используется предположение, что ограничивающиеся рамки не слишком отклоняются от местоположения центра, что обеспечивает стабильность на фоне менее эффективного равномерного выбора рамок-кандидатов по всему исходному изображению. YOLO9000, представленный в той же статье и названный согласно использованию 9000 лучших классов ImageNet, использует древовидную структуру классов, учитывая их вложенность. Например, если среди классов есть метка "Персидская кошка", это будет означать, что найденный объект будет подклассом метки "Кошка". Таким образом, не возникает взаимной исключительности классов, и softmax ко всем классам не применяется. Чтобы предсказать вероятность узла класса, мы можем следовать по пути от узла к корню: | где $x$ {{---}} настоящая ограничивающая рамка, $c_i$ {{---}} центроид кластера. Количество ограничивающих рамок-центроидов выбирается при помощи "метода локтя" (англ. elbow method). Также в YOLOv2 используется предположение, что ограничивающиеся рамки не слишком отклоняются от местоположения центра, что обеспечивает стабильность на фоне менее эффективного равномерного выбора рамок-кандидатов по всему исходному изображению. YOLO9000, представленный в той же статье и названный согласно использованию 9000 лучших классов ImageNet, использует древовидную структуру классов, учитывая их вложенность. Например, если среди классов есть метка "Персидская кошка", это будет означать, что найденный объект будет подклассом метки "Кошка". Таким образом, не возникает взаимной исключительности классов, и softmax ко всем классам не применяется. Чтобы предсказать вероятность узла класса, мы можем следовать по пути от узла к корню: | ||
| − | $p(persian cat|object) = p(persian cat|cat) \cdot p(cat|animal) \cdot p(animal|object) \cdot p(object)$ | + | $p($persian cat$|$object$) = p($persian cat$|$cat$) \cdot p($cat$|$animal$) \cdot p($animal$|$object$) \cdot p($object$)$ |
| − | $p(object)$ {{---}} вероятность обнаружения объекта, вычисленная на этапе генерации ограничительных рамок. Путь прогнозирования условной вероятности может остановиться на любом этапе, в зависимости от того, какие метки доступны. | + | $p($object$)$ {{---}} вероятность обнаружения объекта, вычисленная на этапе генерации ограничительных рамок. Путь прогнозирования условной вероятности может остановиться на любом этапе, в зависимости от того, какие метки доступны. |
YOLOv3<ref>[https://arxiv.org/abs/1804.02767 YOLOv3]</ref>, в свою очередь, является небольшим улучшением YOLOv2 {{---}} используется логистическая регрессия для оценок достоверностей ограничивающих рамок вместо суммы квадратов ошибок для условий классификации в YOLO и YOLOv2; использование нескольких независимых логистических классификаторов для каждого класса вместо одного слоя softmax; добавление межуровневых соединений между уровнями прогнозирования ограничивающих рамок; использование архитектур DarkNet и ResNet для свёрточных сетей. | YOLOv3<ref>[https://arxiv.org/abs/1804.02767 YOLOv3]</ref>, в свою очередь, является небольшим улучшением YOLOv2 {{---}} используется логистическая регрессия для оценок достоверностей ограничивающих рамок вместо суммы квадратов ошибок для условий классификации в YOLO и YOLOv2; использование нескольких независимых логистических классификаторов для каждого класса вместо одного слоя softmax; добавление межуровневых соединений между уровнями прогнозирования ограничивающих рамок; использование архитектур DarkNet и ResNet для свёрточных сетей. | ||
| Строка 136: | Строка 136: | ||
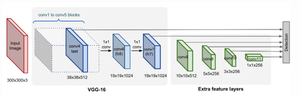
[[Файл:SSD.png|300px|thumb|right|Архитектура нейронной сети для алгоритма SSD]] | [[Файл:SSD.png|300px|thumb|right|Архитектура нейронной сети для алгоритма SSD]] | ||
| − | Модель Single Shot Detector<ref>[https://arxiv.org/abs/1512.02325 Single Shot Detector]</ref> (SSD) использует идею использования пирамидальной иерархии выходов свёрточной сети для эффективного обнаружения объектов различных размеров. Изображение последовательно передаётся на слои свёрточной сети, которые уменьшаются в размерах. Выход из последнего слоя каждой размерности участвует в принятии решения по детекции объектов, таким образом, складывается "пирамидальная характеристика" изображения. Это позволяет обнаруживать объекты различных масштабов, так как размерность выходов первых слоёв сильно коррелирует с ограничивающими рамками для | + | Модель Single Shot Detector<ref>[https://arxiv.org/abs/1512.02325 Single Shot Detector]</ref> (SSD) использует идею использования пирамидальной иерархии выходов свёрточной сети для эффективного обнаружения объектов различных размеров. Изображение последовательно передаётся на слои свёрточной сети, которые уменьшаются в размерах. Выход из последнего слоя каждой размерности участвует в принятии решения по детекции объектов, таким образом, складывается "пирамидальная характеристика" изображения. Это позволяет обнаруживать объекты различных масштабов, так как размерность выходов первых слоёв сильно коррелирует с ограничивающими рамками для маленьких объектов, а последних {{---}} для крупных. В отличие от YOLO, SSD не разбивает изображение на сетку произвольного размера, а предсказывает смещение ключевых рамок. Ключевые рамки на разных уровнях масштабируются так, что одна размерность выходного слоя отвечает за объекты своего масштаба. В результате, большие объекты могут быть обнаружены только на более высоком уровне, а маленькие объекты {{---}} на низких уровнях. Как и в других алгоритмах, функция потерь обеспечивает совместный вклад как потерь локализации, так и потерь классификации. |
| + | |||
| + | ===Anchor boxes=== | ||
| + | |||
| + | Anchor boxes {{---}} алгоритм нахождения объектов, основанный на предсказании категории объекта и отступа от истинной ограничивающей рамки для большого количества сгенерированных ключевых рамок с последующей их фильтрацией. | ||
| + | |||
| + | ====Генерация ключевых рамок==== | ||
| + | |||
| + | Пусть входное изображение имеет высоту $h$ и ширину $w$. Генерируем ключевые рамки с различными формами и размерами, центрированные на каждом пикселе изображения. Предположим, что размер $s∈(0, 1]$, соотношение сторон $r>0$, тогда ширина и высота ключевой рамки равны $ws\sqrt{r}$ и $hs/\sqrt{r}$. Затем определяем набор размеров $s_1,\ldots, s_n$ и набор соотношений $r_1,\ldots, r_m$. Если использовать комбинацию всех размеров и пропорций, то входное изображение будет иметь $whnm$ ключевых рамок, что может привести к большой вычислительной сложности. Поэтому обычно выбираются только комбинации, содержащие размеры $s_1$ и пропорции $r_1$: | ||
| + | |||
| + | $(s_1, r_1), (s_1, r_2), \ldots, (s_1, r_m), (s_2, r_1), (s_3, r_1), \ldots, (s_n, r_1).$ | ||
| + | |||
| + | При таком подходе число рамок для входного изображения сокращается до $wh(n+m-1)$. | ||
| + | |||
| + | ====Процесс обучения==== | ||
| + | |||
| + | Пусть набор ключевых рамок входного изображения это $A_1, A_2, \ldots, A_{n_a}$, а набор истинных ограничивающих рамок это $B_1, B_2, \ldots, B_{n_b}$, и $n_a \geq n_b$. Определяем матрицу $\mathbf{X} \in \mathbb{R}^{n_a \times n_b}$, где элемент $x_{ij}$ - это $IoU$ ключевой рамки $A_i$ с истинной рамкой $B_j$. Затем находим наибольший элемент в матрице $\mathbf{X}$ и сохраняем индекс строки и колонки элемента как $i_1,j_1$. Так мы обозначили ограничивающую рамку $B_{j_1}$ для ключевой рамки $A_{i_1}$. Далее исключаем все элементы в строке с индексом $i_1$ и колонке с индексом $j_1$ в матрице $\mathbf{X}$ для последующих поисков максимального элемента. Теперь ищем наибольший элемент среди оставшихся элементов матрицы $\mathbf{X}$ и сохраняем его индексы как элемент $i_2, j_2$, и также исключаем элементы из соответствующих колонок и строк. | ||
| + | |||
| + | Повторяем данные действия пока все $n_b$ колонки матрицы $\mathbf{X}$ не будут исключены. Затем, для оставшихся $n_a - n_b$ ключевых рамок $A_i$ находим лучшую истинную рамку $B_j$ с наибольшим IoU в строке матрицы $\mathbf{X}$ с индексом $i$. Присваиваем ключевой рамке $A_i$ ограничивающую рамку $B_j$ только если IoU больше предустановленного порогового значения. | ||
| + | |||
| + | Теперь мы можем определить категорию и отступ для каждой ключевой рамки. Если ключевой рамке $\mathbf{A}$ назначена $\mathbf{B}$, то тогда ее категория такая же как и у $\mathbf{B}$. А смещение ключевой рамки $\mathbf{A}$ устанавливается в соответствии с относительным положением центральных координат $\mathbf{B}$ и $\mathbf{A}$ и относительными размерами двух рамок. Поскольку положения и размеры различных рамок в наборе данных могут различаться, эти относительные положения и относительные размеры обычно требуют некоторых специальных преобразований, чтобы сделать распределение смещений более равномерным и более простым для подгонки. Предположим, что центр ключевой рамки $\mathbf{A}$ это $(x_a, y_a)$, высота и ширина это $h_a$ и $w_a$; для $\mathbf{B}$ - $(x_b, y_b)$, $h_b$ и $w_b$ соответственно. В таком случае отступ для A рассчитывается следующим образом: | ||
| + | |||
| + | $\left( \frac{ \frac{x_b - x_a}{w_a} - \mu_x }{\sigma_x}, | ||
| + | \frac{ \frac{y_b - y_a}{h_a} - \mu_y }{\sigma_y}, | ||
| + | \frac{ \log \frac{w_b}{w_a} - \mu_w }{\sigma_w}, | ||
| + | \frac{ \log \frac{h_b}{h_a} - \mu_h }{\sigma_h}\right)$ | ||
| + | |||
| + | Дефолтные значения констант $\mu_x = \mu_y = \mu_w = \mu_h = 0$, $\sigma_x=\sigma_y=0.1$, и $\sigma_w=\sigma_h=0.2$. | ||
| + | |||
| + | Если ключевой рамке не назначен ограничивающий прямоугольник, то устанавливаем категорию background. | ||
| + | |||
| + | ====Процесс предсказаний==== | ||
| + | |||
| + | На этапе прогнозирования сначала генерируется несколько ключевых рамок для изображения, а затем прогнозируются их категории и смещения. Затем на основе ключевых блоков и их прогнозируемых смещений получаются ограничивающие рамки прогнозирования. Когда имеется много ключевых рамок или много одинаковых ограничивающих рамок предсказания могут выводиться несколько раз для одного и того же объекта. Чтобы упростить результаты, можно удалить аналогичные ограничивающие рамки прогнозирования. Обычно используется метод, который называется не максимальное подавление (NMS). | ||
| + | |||
==См.также== | ==См.также== | ||
| Строка 153: | Строка 187: | ||
* [https://github.com/hoya012/deep_learning_object_detection Список статей о детекции объектов методами глубокого обучения] | * [https://github.com/hoya012/deep_learning_object_detection Список статей о детекции объектов методами глубокого обучения] | ||
* [https://towardsdatascience.com/r-cnn-fast-r-cnn-faster-r-cnn-yolo-object-detection-algorithms-36d53571365e R-CNN, Fast R-CNN, Faster R-CNN, YOLO — Object Detection Algorithms] | * [https://towardsdatascience.com/r-cnn-fast-r-cnn-faster-r-cnn-yolo-object-detection-algorithms-36d53571365e R-CNN, Fast R-CNN, Faster R-CNN, YOLO — Object Detection Algorithms] | ||
| + | * [https://d2l.ai/chapter_computer-vision/anchor.html Dive into deep lerning - Computer vision - Anchor Boxes] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
Текущая версия на 19:38, 4 сентября 2022
Задача нахождения объектов на изображении — задача машинного обучения, в рамках которой выполняется определение наличия или отсутствия объекта определённого домена на изображении, нахождение границ этого объекта в системе координат пикселей исходного изображения. В зависимости от алгоритма обучения, объект может характеризоваться координатами ограничивающей рамки, ключевыми точками, контуром объекта.
Постановка задачи
Задача нахождения объектов на изображении может быть поставлена различным образом и включает в себя класс других задач, помогающих определить, какие объекты находятся на изображении и где они расположены в сетке пикселей исходного изображения.
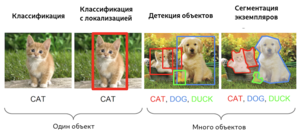
Задача семантической сегментации (англ. semantic segmentation) — задача, в которой на вход модели подаётся изображение, а на выходе для каждого пикселя является метка принадлежности этого пикселя к определённой категории. Например, если в исходном изображении человек переходит дорогу, то для каждого пикселя необходимо вывести, является ли этот пиксель частью человеческого тела, профиля дороги, знака дорожного движения, неба, или какого-то другого типа. Существенный недостаток применения одной лишь семантической сегментации относительно задач, связанных с распознаванием объектов — маркировка пикселей по принадлежности только к типу объекта, что не создаёт различия между объектами как таковыми. Например, если назвать "объектом" связную область пикселей, характеризующих одинаковый тип, то два объекта, перегораживающих друг друга на исходном изображении, будут определены как один объект, что в корне неверно. Задача семантической сегментации изображения с дифференцированием объектов называется задачей сегментации экземпляров (англ. instance segmentation). Модели, решающие задачу сегментации экземпляров, применяются, в том числе, для подсчёта людей в массовых скоплениях, для автомобилей с автоматическим управлением.
Задача классификации с локализацией (англ. classification and localization) — задача, в которой в дополнение к предсказанию метки категории класса определяется рамка, ограничивающая местоположение экземпляра одиночного объекта на картинке. Как правило, рамка имеет прямоугольную форму, её стороны ориентированы параллельно осям исходного изображения, а площадь является минимальной при условии полного нахождения экземпляра объекта внутри этой рамки. Такую прямоугольную рамку называют термином "ограничивающая рамка" (англ. bounding box). Ограничивающую рамку можно задать как при помощи центра, ширины и высоты, так и при помощи четырёх сторон. Модель в данном случается одновременно обучается как верной классификации, так и максимально точному определению границ рамки.
Задача детекции объектов (англ. object detection) — задача, в рамках которой необходимо выделить несколько объектов на изображении посредством нахождения координат их ограничивающих рамок и классификации этих ограничивающих рамок из множества заранее известных классов. В отличие от классификации с локализацией, число объектов, которые находятся на изображении, заведомо неизвестно.
Метрики
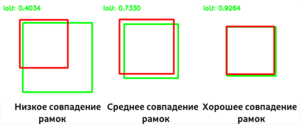
В задачах классификации с локализацией и детекции объектов для определения достоверности местоположения ограничивающей рамки в качестве метрики чаще всего используется отношение площадей ограничивающих рамок (англ. Intersection over Union):
$IoU = \frac{S(A \cap B)}{S(A \cup B)}$,
где $A$ и $B$ — предсказанная ограничивающая рамка и настоящиая ограничивающая рамка соответственно. $IoU$ равно нулю в случае непересекающихся ограничивающих рамок и равно единице в случае идеального наложения.
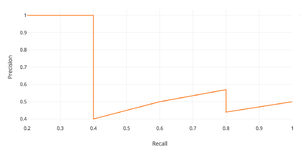
В задачах детекции объектов в качестве метрики зачастую используется $mAP$ (англ. mean average precision) — усреднённая по всем категориям величина средней точности (англ. average precision, AP)
$AP = \int_{0}^{1} p(r) dr$,
где $p$ — точность, $r$ — полнота из предположения, что ограничивающая рамка определена верно, если $IoU \geq 0.5$. Поскольку точность и полнота находятся в промежутке от $0$ до $1$, то $AP$, а следовательно, и $mAP$ также находится в пределах от $0$ до $1$. На практике, $AP$ часто считают по точкам, значения полноты которых равномерно распределены в промежутке $[0;1]$:
$AP_c = \frac{1}{11} \cdot (AP_c(0) + AP_c(0.1) + \ldots + AP_c(1))$
$mAP = \overline{AP_c}$
Наборы данных
Наборы данных в задачах детекции объектов на изображениях размечаются вручную асессорами. Зачастую изображения могут различаться в разрешении и качестве, что может вносить коррективы в работу моделей.
- PASCAL VOC 2012[1] (Pattern Analysis, Statistical Modelling and Computational Learning: Visual Object Classes ) — содержит 11530 изображений 20 классов с 27450 регионами предложений и 6929 сегментациями
- MS COCO 2017[2] (Microsoft Common Objects in Context) — 118000 изображений в тренировочной выборке, 5000 изображений в валидационной выборке, 41000 изображений в тестовой выборке. Набор данных содержит 80 классов, на которых можно определить вложенность
- ImageNet[3] — 400000 изображений 200 классов с 350000 размеченными ограничивающими рамками
- Google Open Images[4] — в шестой версии февраля 2020 года содержит свыше 1743000 изображений в тестовой выборке, свыше 41000 изображений в валидационной выборке и свыше 125000 изображений в тестовой выборке. Суммарно на изображениях размечено около 16000000 ограничивающих рамок
Подходы к решению задачи детекции объектов
Одним из наивных подходов на основе свёрточных нейронных сетей может быть использование в качестве ядра каноничных изображений классов, которые необходимо найти на изображении, и дальнейшее использование скользящего окна для вычисления свёртки. Такой подход называется сопоставлением с шаблоном (англ. template matching). В случае, когда вместо шаблона используется натренированный классификатор, для достижения наилучшего результата необходимо осуществить полный перебор ограничивающих рамок с порогом уверенности в правдивости классификации за счёт того, что объекты могут быть разных масштабов и находиться в разных местах изображений. Однако, на изображении разрешения $W \times H$ суммарное число ограничивающих рамок равно $\sum_{i=0}^{W} \sum_{j=0}^{H} (W-i)\cdot(H-j) = \frac{1}{4} m \cdot n \cdot (m + 1) \cdot (n +1) = O(m^2n^2)$, что делает полный перебор неэффективным методом, занимающим очень большое количество времени. Для уменьшения количества рассматриваемых ограничивающих рамок выделяют два основных параллельно развивающихся подхода:
- Двухэтапные методы (англ. two-stage methods), они же "методы, основанные на регионах" (англ. region-based methods) — подход, разделённый на два этапа. На первом этапе селективным поиском или с помощью специального слоя нейронной сети выделяются регионы интереса (англ. regions of interest, RoI) — области , с высокой вероятностью содержащие внутри себя объекты. На втором этапе выбранные регионы рассматриваются классификатором для определения принадлежности исходным классам и регрессором, уточняющим местоположение ограничивающих рамок.
- Одноэтапные методы (англ. one-stage methods) — подход, не использующий отдельный алгоритм для генерации регионов, вместо этого предсказывая координаты определённого количества ограничивающих рамок с различными характеристиками, такими, как результаты классификации и степень уверенности и в дальнейшем корректируя местоположение рамок.
Двухэтапные методы
R-CNN
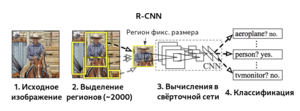
Region-CNN[5] (R-CNN, Region-based Convolutional Network) — алгоритм, основанный на свёрточных нейронных сетях. Вместо того, чтобы использовать для поиска изображений скользящие окна фиксированного размера, на первом шаге алгоритм пытается найти селективным поиском "регионы" — прямоугольные рамки разных размеров, которые, предположительно, содержат объект. Это обеспечивает более быстрое и эффективное нахождение объектов независимо от размера объекта, расстояния до камеры, угла зрения. Суммарное количество регионов для каждого изображения, сгенерированных на первом шаге, примерно равно двум тысячам. Найденные регионы при помощи аффинных преобразований приобретают размер, который нужно подать на вход CNN. Также вместо аффинных преобразований можно использовать паддинги, либо расширять ограничивающие рамки до размеров, необходимых для входа CNN. В качестве CNN зачастую используется архитектура CaffeNet[6], извлекающая для каждого региона порядка 4096 признаков. На последнем этапе вектора признаков регионов обрабатываются SVM, проводящими классификацию объектов, по одной SVM на каждый домен.
Селективный поиск, в свою очередь, тоже можно обучать с помощью линейной регрессии параметров региона — ширины, высоты, центра. Этот метод, названный bounding-box regression, позволяет более точно выделить объект. В качестве данных для регрессии используются признаки, полученные в результате работы CNN.
Fast R-CNN
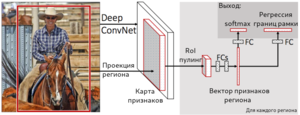
За счёт того, что в R-CNN для каждого из 2000 регионов классификация производится отдельно, обучение сети занимает большой объём времени. Оригинальной версии алгоритма R-CNN для обработки каждого тестового изображения требовалось порядка 47 секунд, поэтому его авторы предложили алгоритм, улучшающий производительность — Fast R-CNN[7]. Его характерной особенностью является подача на вход CNN не отдельных регионов, а всего изображения сразу для получения общей карты признаков. Предложенные регионы накладываются на общую карту признаков, и в результате количество операций свёртки существенно уменьшается. Поскольку регионы имеют разный размер, необходимо привести признаки к фиксированному размеру при помощи операции RoIPooling (Region of interest pooling). В рамках RoIPooling регион делится на сетку, размерность ячеек которой совпадает с размерностью выхода, после чего по ячейкам сетки проводится выбор максимального значения. Полученные регионы фиксированного размера далее являются входом для полносвязного слоя, который и осуществляет как классификацию, так и линейную регрессию для сдвига границ его рамок. Стоит отметить, что в Fast R-CNN используется совместное обучение SVM для классификации, CNN и bounding box регрессора вместо независимого их обучения —для этого используется совместная функция потерь.
Faster R-CNN
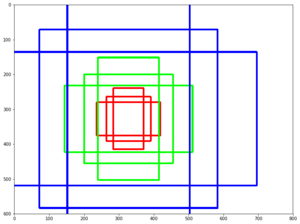
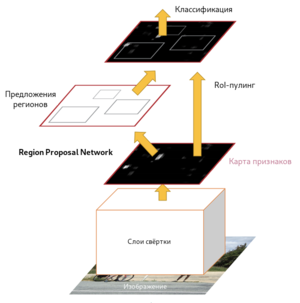
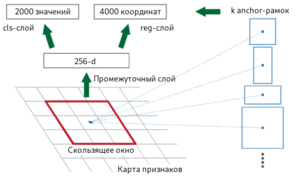
Fast R-CNN, как и оригинальный алгоритм R-CNN, использует для нахождения регионов селективный поиск. Несмотря на то, что за счёт единоразовой свёртки время обучения на одном тестовом изображении алгоритмом снизилось с 49 до 2.3 секунд, селективный поиск, который выполняет предложения регионов, является узким местом в производительности Fast R-CNN. Авторы алгоритма Faster R-CNN[8], призванного решить эту проблему, предложили вычислять регионы с помощью отдельного модуля Region Proposal Network (RPN). RPN является свёрточной сетью, выполняющей роль генератора регионов по признакам исходного изображения. Сгенерированные регионы передаются в два полносвязных слоя — box-regression-layer (сокр. reg layer), прогнозирующий значения смещения для ограничивающих рамок, и box-classification-layer (сокр. cls layer), классифицирующий изображения в пределах предлагаемой области. Также важную роль играют ключевые рамки (англ. anchor boxes) — рамки с различными положениями и размерами для скользящего окна. Ключевые рамки имеют зафиксированное положение и различную форму и масштаб. Для одного и того же масштаба выбирается, как правило, три ключевые рамки — квадратной формы; прямоугольной формы, ориентированной горизонтально; прямоугольной формы, ориентированной вертикально. Учитывая масштаб ключевой рамки, производится его перемещение скользящим окном для генерации регионов. Для сгенерированных таким образом регионов рассчитываются вероятности нахождения объекта внутри рамки cls-слоем, а за сдвиг местоположения отвечает reg-слой. После прохождения слоя RPN следует RoIPooling, как и в алгоритме Fast R-CNN — для преобразования регионов к одному размеру и дальнейшей классификации и смещения границ ограничивающих рамок. Поскольку классификацией и регрессией границ занимается как сеть в целом, так и RPN, предлагающая регионы, функция потерь учитывает как финальное решение по классификации и регрессии координат, так и классификацию и регрессию координат, проведённую RPN.
Mask R-CNN
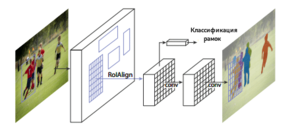
Mask R-CNN[9] — улучшение алгоритма Faster R-CNN, предложенное в 2017 году и обеспечивающее осуществлять возможность сегментации экземпляров объектов, а не только составление ограничивающих рамок с классификацией. В Mask R-CNN к традиционным для алгоритмов семейства R-CNN метке класса и координатам ограничивающей рамки добавляется также маска объекта — прямоугольная матрица принадлежности пикселя текущему объекту. Маски предсказываются для каждого класса с помощью классификации без наличия информации о том, что изображено в регионе, что выдяеляет отдельный классификатор на последнем уровне сети. Потребность предсказания маски обусловила несколько архитектурных изменений относительно Faster R-CNN: ключевым является использование RoIAlign вместо RoIPooling. RoIPooling хорошо подходит для масштабирования ограничивающих рамок, однако, для маски такой метод оказывается недостаточно точным. RoIAlign не использует округлений сдвигов для пулинга, а сохраняет значения с плавающей точкой, используя билинейную интерполяцию. Это обеспечило более точное выделение маски объекта.
Модель Mask R-CNN совершила прорыв в задачах сегментации экземпляров, детекции объектов и определения поз людей на фотографии (англ. human pose estimation). Функция потерь является общей и включает три компонента — классификация, регрессия границ рамки и регрессия значений маски. Это позволило обеспечить взаимопомощь определения сдвигов границ объектов и более точного определения маски.
Одноэтапные методы
Семейство алгоритмов R-CNN использует предсказания регионов, что позволяет обеспечивать хорошую точность, но может быть очень медленным для некоторых сфер, таких, как беспилотное управление автомобилем. Можно выделить ещё одно семейство параллельно развивающихся алгоритмов для детекции изображений, которое не использует регионы — семейство алгоритмов быстрой детекции.
YOLO
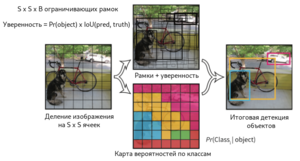
Алгоритм YOLO[10] (You Look Only Once), предложенный в 2016 году, был первой попыткой сделать возможной детекцию объектов в реальном времени. В рамках алгоритма YOLO исходное изображение сначала разбивается на сетку из $N \times N$ ячеек. Если центр объекта попадает внутрь координат ячейки, то эта ячейка считается ответственной за определение параметров местонахождения объекта. Каждая ячейка описывает несколько вариантов местоположения ограничивающих рамок для одного и того же объекта. Каждый из этих вариантов характеризуется пятью значениями — координатами центра ограничивающей рамки, его шириной и высотой, а также степени уверенности в том, что ограничивающая рамка содержит в себе объект. Также необходимо для каждой пары класса объектов и ячейки определить вероятность того, что ячейка содержит в себе объект этого класса. Таким образом, последний слой сети, принимающий конечное решение об ограничивающих рамках и классификации объектов работает с тензором размерности $N \times N \times (5B + C)$, где $B$ — количество предсказываемых ограничивающих рамок для ячейки, $C$ — количество классов объектов, определённых изначально.
Алгоритм YOLO работает быстрее алгоритмов семейства R-CNN за счёт того, что поддерживает дробление на константное количество ячеек вместо того, чтобы предлагать регионы и рассчитывать решение для каждого региона отдельно, однако, в качестве проблем YOLO указывается плохое качество распознавания объектов сложной формы или группы небольших объектов из-за ограниченного числа кандидатов для ограничивающих рамок.
YOLOv2, YOLOv3
Улучшенная версия модели YOLOv2[11] отличается от предшественницы использованием батчевой нормализации на свёрточных слоях, обучением модели на изображениях с повышенным разрешением, использованием ключевых рамок для предсказания местонахождения объектов, использованием кластеризации алгоримтом $k$-средних для обучения более эффективного выбора размеров ограничивающих рамок на тренировочной выборке с использованием функции расстояния на основе IoU:
$dist(x, c_i) = 1 - IoU(x, c_i)$
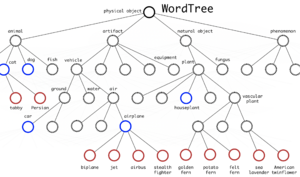
где $x$ — настоящая ограничивающая рамка, $c_i$ — центроид кластера. Количество ограничивающих рамок-центроидов выбирается при помощи "метода локтя" (англ. elbow method). Также в YOLOv2 используется предположение, что ограничивающиеся рамки не слишком отклоняются от местоположения центра, что обеспечивает стабильность на фоне менее эффективного равномерного выбора рамок-кандидатов по всему исходному изображению. YOLO9000, представленный в той же статье и названный согласно использованию 9000 лучших классов ImageNet, использует древовидную структуру классов, учитывая их вложенность. Например, если среди классов есть метка "Персидская кошка", это будет означать, что найденный объект будет подклассом метки "Кошка". Таким образом, не возникает взаимной исключительности классов, и softmax ко всем классам не применяется. Чтобы предсказать вероятность узла класса, мы можем следовать по пути от узла к корню:
$p($persian cat$|$object$) = p($persian cat$|$cat$) \cdot p($cat$|$animal$) \cdot p($animal$|$object$) \cdot p($object$)$
$p($object$)$ — вероятность обнаружения объекта, вычисленная на этапе генерации ограничительных рамок. Путь прогнозирования условной вероятности может остановиться на любом этапе, в зависимости от того, какие метки доступны.
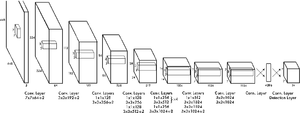
YOLOv3[12], в свою очередь, является небольшим улучшением YOLOv2 — используется логистическая регрессия для оценок достоверностей ограничивающих рамок вместо суммы квадратов ошибок для условий классификации в YOLO и YOLOv2; использование нескольких независимых логистических классификаторов для каждого класса вместо одного слоя softmax; добавление межуровневых соединений между уровнями прогнозирования ограничивающих рамок; использование архитектур DarkNet и ResNet для свёрточных сетей.
SSD
Модель Single Shot Detector[13] (SSD) использует идею использования пирамидальной иерархии выходов свёрточной сети для эффективного обнаружения объектов различных размеров. Изображение последовательно передаётся на слои свёрточной сети, которые уменьшаются в размерах. Выход из последнего слоя каждой размерности участвует в принятии решения по детекции объектов, таким образом, складывается "пирамидальная характеристика" изображения. Это позволяет обнаруживать объекты различных масштабов, так как размерность выходов первых слоёв сильно коррелирует с ограничивающими рамками для маленьких объектов, а последних — для крупных. В отличие от YOLO, SSD не разбивает изображение на сетку произвольного размера, а предсказывает смещение ключевых рамок. Ключевые рамки на разных уровнях масштабируются так, что одна размерность выходного слоя отвечает за объекты своего масштаба. В результате, большие объекты могут быть обнаружены только на более высоком уровне, а маленькие объекты — на низких уровнях. Как и в других алгоритмах, функция потерь обеспечивает совместный вклад как потерь локализации, так и потерь классификации.
Anchor boxes
Anchor boxes — алгоритм нахождения объектов, основанный на предсказании категории объекта и отступа от истинной ограничивающей рамки для большого количества сгенерированных ключевых рамок с последующей их фильтрацией.
Генерация ключевых рамок
Пусть входное изображение имеет высоту $h$ и ширину $w$. Генерируем ключевые рамки с различными формами и размерами, центрированные на каждом пикселе изображения. Предположим, что размер $s∈(0, 1]$, соотношение сторон $r>0$, тогда ширина и высота ключевой рамки равны $ws\sqrt{r}$ и $hs/\sqrt{r}$. Затем определяем набор размеров $s_1,\ldots, s_n$ и набор соотношений $r_1,\ldots, r_m$. Если использовать комбинацию всех размеров и пропорций, то входное изображение будет иметь $whnm$ ключевых рамок, что может привести к большой вычислительной сложности. Поэтому обычно выбираются только комбинации, содержащие размеры $s_1$ и пропорции $r_1$:
$(s_1, r_1), (s_1, r_2), \ldots, (s_1, r_m), (s_2, r_1), (s_3, r_1), \ldots, (s_n, r_1).$
При таком подходе число рамок для входного изображения сокращается до $wh(n+m-1)$.
Процесс обучения
Пусть набор ключевых рамок входного изображения это $A_1, A_2, \ldots, A_{n_a}$, а набор истинных ограничивающих рамок это $B_1, B_2, \ldots, B_{n_b}$, и $n_a \geq n_b$. Определяем матрицу $\mathbf{X} \in \mathbb{R}^{n_a \times n_b}$, где элемент $x_{ij}$ - это $IoU$ ключевой рамки $A_i$ с истинной рамкой $B_j$. Затем находим наибольший элемент в матрице $\mathbf{X}$ и сохраняем индекс строки и колонки элемента как $i_1,j_1$. Так мы обозначили ограничивающую рамку $B_{j_1}$ для ключевой рамки $A_{i_1}$. Далее исключаем все элементы в строке с индексом $i_1$ и колонке с индексом $j_1$ в матрице $\mathbf{X}$ для последующих поисков максимального элемента. Теперь ищем наибольший элемент среди оставшихся элементов матрицы $\mathbf{X}$ и сохраняем его индексы как элемент $i_2, j_2$, и также исключаем элементы из соответствующих колонок и строк.
Повторяем данные действия пока все $n_b$ колонки матрицы $\mathbf{X}$ не будут исключены. Затем, для оставшихся $n_a - n_b$ ключевых рамок $A_i$ находим лучшую истинную рамку $B_j$ с наибольшим IoU в строке матрицы $\mathbf{X}$ с индексом $i$. Присваиваем ключевой рамке $A_i$ ограничивающую рамку $B_j$ только если IoU больше предустановленного порогового значения.
Теперь мы можем определить категорию и отступ для каждой ключевой рамки. Если ключевой рамке $\mathbf{A}$ назначена $\mathbf{B}$, то тогда ее категория такая же как и у $\mathbf{B}$. А смещение ключевой рамки $\mathbf{A}$ устанавливается в соответствии с относительным положением центральных координат $\mathbf{B}$ и $\mathbf{A}$ и относительными размерами двух рамок. Поскольку положения и размеры различных рамок в наборе данных могут различаться, эти относительные положения и относительные размеры обычно требуют некоторых специальных преобразований, чтобы сделать распределение смещений более равномерным и более простым для подгонки. Предположим, что центр ключевой рамки $\mathbf{A}$ это $(x_a, y_a)$, высота и ширина это $h_a$ и $w_a$; для $\mathbf{B}$ - $(x_b, y_b)$, $h_b$ и $w_b$ соответственно. В таком случае отступ для A рассчитывается следующим образом:
$\left( \frac{ \frac{x_b - x_a}{w_a} - \mu_x }{\sigma_x}, \frac{ \frac{y_b - y_a}{h_a} - \mu_y }{\sigma_y}, \frac{ \log \frac{w_b}{w_a} - \mu_w }{\sigma_w}, \frac{ \log \frac{h_b}{h_a} - \mu_h }{\sigma_h}\right)$
Дефолтные значения констант $\mu_x = \mu_y = \mu_w = \mu_h = 0$, $\sigma_x=\sigma_y=0.1$, и $\sigma_w=\sigma_h=0.2$.
Если ключевой рамке не назначен ограничивающий прямоугольник, то устанавливаем категорию background.
Процесс предсказаний
На этапе прогнозирования сначала генерируется несколько ключевых рамок для изображения, а затем прогнозируются их категории и смещения. Затем на основе ключевых блоков и их прогнозируемых смещений получаются ограничивающие рамки прогнозирования. Когда имеется много ключевых рамок или много одинаковых ограничивающих рамок предсказания могут выводиться несколько раз для одного и того же объекта. Чтобы упростить результаты, можно удалить аналогичные ограничивающие рамки прогнозирования. Обычно используется метод, который называется не максимальное подавление (NMS).
См.также
Примечания
Источники информации
- Stanford CS231n: Detection and Segmentation
- Stepik.org: Deep Learning School
- Habr: обзор Deep Learning в Computer Vision
- Список статей о детекции объектов методами глубокого обучения
- R-CNN, Fast R-CNN, Faster R-CNN, YOLO — Object Detection Algorithms
- Dive into deep lerning - Computer vision - Anchor Boxes