Многопоточность в машинном обучении — различия между версиями
(Статья, первый вид) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 27 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Для применения машинного обучения на практике часто нужно обработать большое количество данных и на это уходит много времени. Использование многопоточности и других видов параллелизма позволяет значительно ускорить вычисления, иногда даже без изменения самого алгоритма. | ||
| + | |||
Следует выделить следующие виды параллелизма: | Следует выделить следующие виды параллелизма: | ||
| − | * Параллелизм на уровне инструкций (ILP): | + | * Параллелизм на уровне инструкций (англ. instruction-level parallelism, ILP<ref>[https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%B8%D0%B7%D0%BC_%D0%BD%D0%B0_%D1%83%D1%80%D0%BE%D0%B2%D0%BD%D0%B5_%D0%BA%D0%BE%D0%BC%D0%B0%D0%BD%D0%B4 ILP]</ref>): несколько инструкций исполняются одновременно. |
| − | * Параллелизм одна инструкция множество данных(SIMD): одна | + | * Параллелизм типа одна инструкция множество данных (англ. single instruction, multiple data, SIMD<ref>[https://ru.wikipedia.org/wiki/SIMD SIMD]</ref>): одна операция применяется к множеству данных. |
* Многопоточный параллелизм: несколько независимых рабочих потоков взаимодействуют через абстракцию совместно используемой памяти. | * Многопоточный параллелизм: несколько независимых рабочих потоков взаимодействуют через абстракцию совместно используемой памяти. | ||
| − | * Распределенные вычисления: несколько независимых рабочих компьютеров взаимодействуют по сети. | + | * Распределенные вычисления: несколько независимых рабочих компьютеров взаимодействуют по сети (MLlib<ref>[https://spark.apache.org/mllib/ MLlib]</ref> на Spark, Mahout<ref>[https://mahout.apache.org/ Mahout]</ref> на Hadoop). |
| + | |||
| + | == Идеи используемые для ускорения вычислений в машинном обучении == | ||
| + | === Параллелизм для ускорения линейной алгебры === | ||
| + | Многие операции линейной алгебры, например, векторное сложение, произведение матриц и вычисление нормы состоят из большого количества независимых операций. Поэтому можно сильно повысить их производительность как за счёт ILP и SIMD параллелизма для маленьких данных, так и за счёт многопоточности для больших данных. От ускорения линейной алгебры особенно выигрывают нейронные сети, так как большую часть времени их работы занимает умножение матриц. | ||
| − | + | Некоторые действия, выполняемые в цикле, можно записать как операции над матрицами, полученными повторением матриц меньшей размерности. Например, сложение каждой строки матрицы с вектором {{---}} это сложение двух матриц, в одной из которых повторяются строки. Бродкастинг (англ. broadcasting<ref>[https://numpy.org/doc/stable/user/basics.broadcasting.html Broadcasting {{---}} NumPy v1.19 Manual]</ref><ref>[https://octave.org/doc/v6.1.0/Broadcasting.html Broadcasting (GNU Octave (version 6.1.0))]</ref>) позволяет выполнять операции с аргуметами разных размерностей, неявно приводя их к одной. При этом из пользовательского кода исчезают циклы, а задача оптимизации переходит к разработчику библиотеки, который может обеспечить лучший параллелизм операций за счет доступа к внутренностям библиотеки. | |
| − | |||
| − | |||
Примеры оптимизаций: | Примеры оптимизаций: | ||
* Высоко оптимизированные тензорные библиотеки для арифметики. | * Высоко оптимизированные тензорные библиотеки для арифметики. | ||
* Алгоритмы в терминах матричных операций, а не векторных операций, насколько это возможно. | * Алгоритмы в терминах матричных операций, а не векторных операций, насколько это возможно. | ||
| − | * | + | * Бродкастинг вместо циклов. |
| − | * Распараллеленные реализации некоторых специальных операций (таких как свертки для | + | * Распараллеленные реализации некоторых специальных операций (таких как свертки для [[Сверточные нейронные сети | сверточных сетей]]). |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Параллелизм в оптимизации гиперпараметров === | === Параллелизм в оптимизации гиперпараметров === | ||
| − | Для параллельной оптимизации | + | Для параллельной [[Настройка гиперпараметров | оптимизации гиперпараметров]] можно использовать поиск по решётке или случайный поиск в которых мы можем оценить параметры независимо. |
Такая оптимизации часто встречаются в библиотеках машинного обучения. | Такая оптимизации часто встречаются в библиотеках машинного обучения. | ||
=== Параллелизм кросс-валидации === | === Параллелизм кросс-валидации === | ||
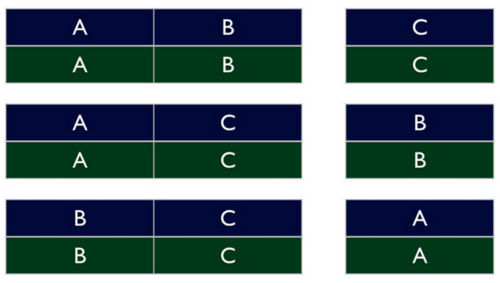
| − | Полная кросс-валидация, k-fold, t×k-fold, Leave-One-Out легко распараллеливаются на несколько потоков, каждый из которых работает на своем разбиении данных | + | Полная [[Кросс-валидация | кросс-валидация]], k-fold, t×k-fold, Leave-One-Out легко распараллеливаются на несколько потоков, каждый из которых работает на своем разбиении данных |
[[Файл:ParallelCrossValidation.png|500px]] | [[Файл:ParallelCrossValidation.png|500px]] | ||
| − | === Параллелизм GPU === | + | === Параллелизм GPU<ref>[https://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%BE%D1%80 GPU]</ref> === |
| − | + | Графические процессоры позволяют применять одну и ту же операцию параллельно к десяткам тысяч элементов за счет большого числа потоков. | |
| − | |||
| − | |||
| − | |||
| − | + | Фреймворки машинного обучения, такие как TensorFlow, PyTorch и MxNet используют эти возможности через библиотеки от компаний производителей графических ускорителей и открытые фреймворки: | |
| − | + | * CUDA<ref>[https://developer.nvidia.com/cuda-toolkit CUDA]</ref> {{---}} язык параллельного программирования/вычислительная платформа для вычислений общего назначения на графическом процессоре | |
| − | + | * cuBLAS<ref>[https://developer.nvidia.com/cublas cuBLAS]</ref> {{---}} библиотека представляет собой реализацию базовых подпрограмм линейной алгебры (англ. Basic Linear Algebra Subprograms, BLAS) поверх среды выполнения CUDA. | |
| + | * OpenCL<ref>[https://www.khronos.org/opencl/ OpenCL]</ref> {{---}} фреймворк для написания компьютерных программ, связанных с параллельными вычислениями на различных графических и центральных процессорах, а также программируемых пользователем вентильных матрицах (ППВМ, англ. field-programmable gate array, FPGA<ref>[https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D1%83%D0%B5%D0%BC%D0%B0%D1%8F_%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D0%B5%D0%BC_%D0%B2%D0%B5%D0%BD%D1%82%D0%B8%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 Программируемая пользователем вентильная матрица]</ref>). | ||
| + | Пример перемножения матриц на C с использованием cuBLAS: | ||
| + | <font color="#B00040">void</font> <font color="#0000FF">gpu_blas_mmul</font>(cublasHandle_t &handle, <font color="#008000">'''const'''</font> <font color="#B00040">float</font> *A, <font color="#008000">'''const'''</font> <font color="#B00040">float</font> *B, <font color="#B00040">float</font> *C, <font color="#008000">'''const'''</font> <font color="#B00040">int</font> m, <font color="#008000">'''const'''</font> <font color="#B00040">int</font> k, <font color="#008000">'''const'''</font> <font color="#B00040">int</font> n) { | ||
| + | <font color="#B00040">int</font> lda = m, ldb = k, ldc = m; | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">float</font> alf = 1; | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">float</font> bet = 0; | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">float</font> *alpha = &alf; | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">float</font> *beta = &bet; | ||
| + | <font color="#408080">''// Do the actual multiplication''</font> | ||
| + | cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, alpha, A, lda, B, ldb, beta, C, ldc); | ||
| + | } | ||
| + | |||
| + | Пример перемножения матриц на питоне с использованием PyCUDA: | ||
| + | <font color="#008000">'''import'''</font> <font color="#0000FF">'''pycuda.gpuarray'''</font> <font color="#008000">'''as'''</font> <font color="#0000FF">'''gpuarray'''</font> | ||
| + | <font color="#008000">'''import'''</font> <font color="#0000FF">'''numpy'''</font> <font color="#008000">'''as'''</font> <font color="#0000FF">'''np'''</font> | ||
| + | <font color="#008000">'''import'''</font> <font color="#0000FF">'''skcuda.linalg'''</font> <font color="#008000">'''as'''</font> <font color="#0000FF">'''linalg'''</font> | ||
| + | <font color="#408080">''# --- Initializations''</font> | ||
| + | <font color="#008000">'''import'''</font> <font color="#0000FF">'''pycuda.autoinit'''</font> | ||
| + | linalg.init() | ||
| + | |||
| + | A = np.array(([1, 2, 3], [4, 5, 6])).astype(np.float64) | ||
| + | B = np.array(([7, 8, 1, 5], [9, 10, 0, 9], [11, 12, 5, 5])).astype(np.float64) | ||
| + | |||
| + | A_gpu = gpuarray.to_gpu(A) | ||
| + | B_gpu = gpuarray.to_gpu(B) | ||
| + | |||
| + | C_gpu = linalg.dot(A_gpu, B_gpu) | ||
| + | |||
| + | <font color="#008000">print</font>(np.dot(A, B)) | ||
| + | <font color="#008000">print</font>(C_gpu) | ||
| + | |||
| + | Наивная реализация перемножения матриц на OpenCL: | ||
| + | <font color="#408080">''// First naive implementation''</font> | ||
| + | __kernel <font color="#B00040">void</font> myGEMM1(<font color="#008000">'''const'''</font> <font color="#B00040">int</font> M, <font color="#008000">'''const'''</font> <font color="#B00040">int</font> N, <font color="#008000">'''const'''</font> <font color="#B00040">int</font> K, | ||
| + | <font color="#008000">'''const'''</font> __global <font color="#B00040">float</font> *A, | ||
| + | <font color="#008000">'''const'''</font> __global <font color="#B00040">float</font> *B, | ||
| + | __global <font color="#B00040">float</font> *C) { | ||
| + | |||
| + | <font color="#408080">''// Thread identifiers''</font> | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">int</font> globalRow = get_global_id(0); <font color="#408080">''// Row ID of C (0..M)''</font> | ||
| + | <font color="#008000">'''const'''</font> <font color="#B00040">int</font> globalCol = get_global_id(1); <font color="#408080">''// Col ID of C (0..N)''</font> | ||
| + | |||
| + | <font color="#408080">''// Compute a single element (loop over K)''</font> | ||
| + | <font color="#B00040">float</font> acc = 0.0f; | ||
| + | <font color="#008000">'''for'''</font> (<font color="#B00040">int</font> k = 0; k < K; k++) { | ||
| + | acc += A[k * M + globalRow] * B[globalCol * K + k]; | ||
| + | } | ||
| + | |||
| + | <font color="#408080">''// Store the result''</font> | ||
| + | C[globalCol * M + globalRow] = acc; | ||
| + | } | ||
| + | === Параллелизм в стохастическом градиентном спуске === | ||
| + | Можно запустить внешний цикл [[Стохастический градиентный спуск|стохастического градиентного спуска (SGD)]] параллельно в пуле потоков и использовать конструкции синхронизации, такие как блокировки, чтобы предотвратить состояние гонки. Однако из-за накладных расходов на синхронизацию ускорение может получиться маленьким. | ||
| + | |||
| + | Еще более интересная идея называется асинхронным SGD или Hogwild<ref>[https://arxiv.org/abs/1106.5730 Feng Niu, Benjamin Recht, Christopher Re, Stephen J. Wright (2011) HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent]</ref>. | ||
| + | SGD запускается параллельно в несколько потоков без какой-либо синхронизации. Теперь состояния гонки могут возникнуть, но во многих случаях это хорошо, потому что они просто немного изменяют шум и ошибки уже присутствующие из-за случайного выбора градиента. | ||
| + | |||
| + | === Параллелизм в методе k ближайших соседей === | ||
| + | Основное время работы [[Метрический классификатор и метод ближайших соседей|метода k ближайших соседей]] составляет поиск ближайших соседей. | ||
| + | Так как расстояния до разных объектов независимы, то можно разбить объекты на группы, параллельно решить задачу во всех группах, а потом объединить результат<ref>[http://ceres-journal.eu/download.php?file=2019_01_01.pdf Ahmed S. J. Abu Hammad (2019) Implementation of a Parallel K-Nearest Neighbor Algorithm Using MPI]</ref>. | ||
| + | Альтернативный подход {{---}} параллельная сортировка всех объектов, например, с использованием битонной сортировки<ref>[https://users.cs.duke.edu/~nikos/reprints/knn-TR-CS-2012-03.pdf Nikos Sismanis, Nikos P. Pitsianis, Xiaobai Sun (2012) Parallel Search of k-Nearest Neighbors with Synchronous Operations]</ref>. | ||
| + | |||
| + | === Параллелизм в методе опорных векторов === | ||
| + | Вычислительная сложность [[Метод опорных векторов (SVM)|метода опорных векторов]] заключается в минимизации квадратичной функции. | ||
| + | Первый вариант распараллеливания задачи {{---}} добавление параллелизма в алгоритм в явном виде, например, параллельная оптимизация большего количества переменных в SMO<ref>[https://publikationen.uni-tuebingen.de/xmlui/bitstream/handle/10900/49015/pdf/tech_21.pdf Dominik Brugger (2006) Parallel Support Vector Machines]</ref>. | ||
| + | Второй подход {{---}} запись алгоритма через матричные операции, которые легко параллелизируемы, например, можно обновлять вектор из оптимизируемых параметров через умножение на матрицы<ref>[https://www.researchgate.net/publication/6265163_Multiplicative_Updates_for_Nonnegative_Quadratic_Programming Fei Sha, Yuanqing Lin, Lawrence K. Saul, Daniel D. Lee (2006) Multiplicative Updates for Nonnegative Quadratic Programming]</ref>. | ||
| + | |||
| + | === Параллелизм в линейной регрессии === | ||
| + | При использовании [[Линейная регрессия | метода наименьших квадратов]] поиск коэффициентов регрессии сводится к нахождению псевдообратной матрицы. Хотя псевдообратную матрицу можно вычислить через обратную и для этого существуют параллельные алгоритмы, такой подход остается непрактичным. Более популярный способ, основанный на сингулярном разложении, можно сделать параллельным, если в процессе использовать метод Якоби для собственных значений и на каждом шаге обрабатывать несколько строк и столбцов<ref>[https://www.irisa.fr/sage/bernard/publis/SVD-Chapter06.pdf Handbook of Parallel Computing and Statistics: Parallel Algorithms for the Singular Value Decomposition]</ref>. Также можно использовать параллельный алгоритм для QR-разложения как это сделано в ScaLAPACK<ref>[https://web.archive.org/web/20181004072955/http://www.netlib.org/scalapack/slug/node45.html#1004 ScaLAPACK {{---}} Linear Least Squares Problems]</ref>. | ||
| + | |||
| + | ==См. также== | ||
| + | *[[Стохастический градиентный спуск]] | ||
| + | *[[Кросс-валидация]] | ||
| + | *[[Настройка гиперпараметров]] | ||
| + | *[[Метод опорных векторов (SVM)]] | ||
| + | *[[Метрический классификатор и метод ближайших соседей]] | ||
| + | == Примечания == | ||
| + | <references/> | ||
== Источники информации == | == Источники информации == | ||
# [http://www.cs.cornell.edu/courses/cs4787/2019sp/notes/lecture1.pdf Principles of Large-Scale Machine Learning] | # [http://www.cs.cornell.edu/courses/cs4787/2019sp/notes/lecture1.pdf Principles of Large-Scale Machine Learning] | ||
| − | + | # [https://docs.nvidia.com/cuda/pdf/CUBLAS_Library.pdf cuBLAS library user guide] | |
| + | # [https://solarianprogrammer.com/2012/05/31/matrix-multiplication-cuda-cublas-curand-thrust/ Matrix multiplication on GPU using CUDA with CUBLAS] | ||
| + | # [https://medium.com/@CIulius/a-short-notice-on-performing-matrix-multiplications-in-pycuda-cbfb00cf1450 A short notice on performing matrix multiplications in PyCUDA] | ||
| + | # [https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html CUDA C++ Programming Guide] | ||
| + | # [https://cnugteren.github.io/tutorial/pages/page1.html OpenCL SGEMM tuning for Kepler] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
Текущая версия на 19:19, 4 сентября 2022
Для применения машинного обучения на практике часто нужно обработать большое количество данных и на это уходит много времени. Использование многопоточности и других видов параллелизма позволяет значительно ускорить вычисления, иногда даже без изменения самого алгоритма.
Следует выделить следующие виды параллелизма:
- Параллелизм на уровне инструкций (англ. instruction-level parallelism, ILP[1]): несколько инструкций исполняются одновременно.
- Параллелизм типа одна инструкция множество данных (англ. single instruction, multiple data, SIMD[2]): одна операция применяется к множеству данных.
- Многопоточный параллелизм: несколько независимых рабочих потоков взаимодействуют через абстракцию совместно используемой памяти.
- Распределенные вычисления: несколько независимых рабочих компьютеров взаимодействуют по сети (MLlib[3] на Spark, Mahout[4] на Hadoop).
Содержание
- 1 Идеи используемые для ускорения вычислений в машинном обучении
- 1.1 Параллелизм для ускорения линейной алгебры
- 1.2 Параллелизм в оптимизации гиперпараметров
- 1.3 Параллелизм кросс-валидации
- 1.4 Параллелизм GPU[7]
- 1.5 Параллелизм в стохастическом градиентном спуске
- 1.6 Параллелизм в методе k ближайших соседей
- 1.7 Параллелизм в методе опорных векторов
- 1.8 Параллелизм в линейной регрессии
- 2 См. также
- 3 Примечания
- 4 Источники информации
Идеи используемые для ускорения вычислений в машинном обучении
Параллелизм для ускорения линейной алгебры
Многие операции линейной алгебры, например, векторное сложение, произведение матриц и вычисление нормы состоят из большого количества независимых операций. Поэтому можно сильно повысить их производительность как за счёт ILP и SIMD параллелизма для маленьких данных, так и за счёт многопоточности для больших данных. От ускорения линейной алгебры особенно выигрывают нейронные сети, так как большую часть времени их работы занимает умножение матриц.
Некоторые действия, выполняемые в цикле, можно записать как операции над матрицами, полученными повторением матриц меньшей размерности. Например, сложение каждой строки матрицы с вектором — это сложение двух матриц, в одной из которых повторяются строки. Бродкастинг (англ. broadcasting[5][6]) позволяет выполнять операции с аргуметами разных размерностей, неявно приводя их к одной. При этом из пользовательского кода исчезают циклы, а задача оптимизации переходит к разработчику библиотеки, который может обеспечить лучший параллелизм операций за счет доступа к внутренностям библиотеки.
Примеры оптимизаций:
- Высоко оптимизированные тензорные библиотеки для арифметики.
- Алгоритмы в терминах матричных операций, а не векторных операций, насколько это возможно.
- Бродкастинг вместо циклов.
- Распараллеленные реализации некоторых специальных операций (таких как свертки для сверточных сетей).
Параллелизм в оптимизации гиперпараметров
Для параллельной оптимизации гиперпараметров можно использовать поиск по решётке или случайный поиск в которых мы можем оценить параметры независимо. Такая оптимизации часто встречаются в библиотеках машинного обучения.
Параллелизм кросс-валидации
Полная кросс-валидация, k-fold, t×k-fold, Leave-One-Out легко распараллеливаются на несколько потоков, каждый из которых работает на своем разбиении данных
Параллелизм GPU[7]
Графические процессоры позволяют применять одну и ту же операцию параллельно к десяткам тысяч элементов за счет большого числа потоков.
Фреймворки машинного обучения, такие как TensorFlow, PyTorch и MxNet используют эти возможности через библиотеки от компаний производителей графических ускорителей и открытые фреймворки:
- CUDA[8] — язык параллельного программирования/вычислительная платформа для вычислений общего назначения на графическом процессоре
- cuBLAS[9] — библиотека представляет собой реализацию базовых подпрограмм линейной алгебры (англ. Basic Linear Algebra Subprograms, BLAS) поверх среды выполнения CUDA.
- OpenCL[10] — фреймворк для написания компьютерных программ, связанных с параллельными вычислениями на различных графических и центральных процессорах, а также программируемых пользователем вентильных матрицах (ППВМ, англ. field-programmable gate array, FPGA[11]).
Пример перемножения матриц на C с использованием cuBLAS:
void gpu_blas_mmul(cublasHandle_t &handle, const float *A, const float *B, float *C, const int m, const int k, const int n) {
int lda = m, ldb = k, ldc = m;
const float alf = 1;
const float bet = 0;
const float *alpha = &alf;
const float *beta = &bet;
// Do the actual multiplication
cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, alpha, A, lda, B, ldb, beta, C, ldc);
}
Пример перемножения матриц на питоне с использованием PyCUDA:
import pycuda.gpuarray as gpuarray import numpy as np import skcuda.linalg as linalg # --- Initializations import pycuda.autoinit linalg.init() A = np.array(([1, 2, 3], [4, 5, 6])).astype(np.float64) B = np.array(([7, 8, 1, 5], [9, 10, 0, 9], [11, 12, 5, 5])).astype(np.float64) A_gpu = gpuarray.to_gpu(A) B_gpu = gpuarray.to_gpu(B) C_gpu = linalg.dot(A_gpu, B_gpu) print(np.dot(A, B)) print(C_gpu)
Наивная реализация перемножения матриц на OpenCL:
// First naive implementation
__kernel void myGEMM1(const int M, const int N, const int K,
const __global float *A,
const __global float *B,
__global float *C) {
// Thread identifiers
const int globalRow = get_global_id(0); // Row ID of C (0..M)
const int globalCol = get_global_id(1); // Col ID of C (0..N)
// Compute a single element (loop over K)
float acc = 0.0f;
for (int k = 0; k < K; k++) {
acc += A[k * M + globalRow] * B[globalCol * K + k];
}
// Store the result
C[globalCol * M + globalRow] = acc;
}
Параллелизм в стохастическом градиентном спуске
Можно запустить внешний цикл стохастического градиентного спуска (SGD) параллельно в пуле потоков и использовать конструкции синхронизации, такие как блокировки, чтобы предотвратить состояние гонки. Однако из-за накладных расходов на синхронизацию ускорение может получиться маленьким.
Еще более интересная идея называется асинхронным SGD или Hogwild[12]. SGD запускается параллельно в несколько потоков без какой-либо синхронизации. Теперь состояния гонки могут возникнуть, но во многих случаях это хорошо, потому что они просто немного изменяют шум и ошибки уже присутствующие из-за случайного выбора градиента.
Параллелизм в методе k ближайших соседей
Основное время работы метода k ближайших соседей составляет поиск ближайших соседей. Так как расстояния до разных объектов независимы, то можно разбить объекты на группы, параллельно решить задачу во всех группах, а потом объединить результат[13]. Альтернативный подход — параллельная сортировка всех объектов, например, с использованием битонной сортировки[14].
Параллелизм в методе опорных векторов
Вычислительная сложность метода опорных векторов заключается в минимизации квадратичной функции. Первый вариант распараллеливания задачи — добавление параллелизма в алгоритм в явном виде, например, параллельная оптимизация большего количества переменных в SMO[15]. Второй подход — запись алгоритма через матричные операции, которые легко параллелизируемы, например, можно обновлять вектор из оптимизируемых параметров через умножение на матрицы[16].
Параллелизм в линейной регрессии
При использовании метода наименьших квадратов поиск коэффициентов регрессии сводится к нахождению псевдообратной матрицы. Хотя псевдообратную матрицу можно вычислить через обратную и для этого существуют параллельные алгоритмы, такой подход остается непрактичным. Более популярный способ, основанный на сингулярном разложении, можно сделать параллельным, если в процессе использовать метод Якоби для собственных значений и на каждом шаге обрабатывать несколько строк и столбцов[17]. Также можно использовать параллельный алгоритм для QR-разложения как это сделано в ScaLAPACK[18].
См. также
- Стохастический градиентный спуск
- Кросс-валидация
- Настройка гиперпараметров
- Метод опорных векторов (SVM)
- Метрический классификатор и метод ближайших соседей
Примечания
- ↑ ILP
- ↑ SIMD
- ↑ MLlib
- ↑ Mahout
- ↑ Broadcasting — NumPy v1.19 Manual
- ↑ Broadcasting (GNU Octave (version 6.1.0))
- ↑ GPU
- ↑ CUDA
- ↑ cuBLAS
- ↑ OpenCL
- ↑ Программируемая пользователем вентильная матрица
- ↑ Feng Niu, Benjamin Recht, Christopher Re, Stephen J. Wright (2011) HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent
- ↑ Ahmed S. J. Abu Hammad (2019) Implementation of a Parallel K-Nearest Neighbor Algorithm Using MPI
- ↑ Nikos Sismanis, Nikos P. Pitsianis, Xiaobai Sun (2012) Parallel Search of k-Nearest Neighbors with Synchronous Operations
- ↑ Dominik Brugger (2006) Parallel Support Vector Machines
- ↑ Fei Sha, Yuanqing Lin, Lawrence K. Saul, Daniel D. Lee (2006) Multiplicative Updates for Nonnegative Quadratic Programming
- ↑ Handbook of Parallel Computing and Statistics: Parallel Algorithms for the Singular Value Decomposition
- ↑ ScaLAPACK — Linear Least Squares Problems