Обсуждение:Подсчет деревьев — различия между версиями
Egor Ba (обсуждение | вклад) |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
{{Утверждение | {{Утверждение | ||
| − | |statement=Число помеченных корневых деревьев с <tex>k</tex> листьями и <tex>m</tex> вершинами есть <tex>P_{m,k} = k\cdot P_{m-1,k}+(m-k))\cdot P_{m-1,k-1}</tex>.<br> | + | |statement=Число помеченных корневых деревьев с <tex>k</tex> листьями и <tex>m</tex> вершинами, у которых номер предка меньше номера вершины, есть <tex>P_{m,k} = k\cdot P_{m-1,k}+(m-k))\cdot P_{m-1,k-1}</tex>.<br> |
| − | |||
|proof = | |proof = | ||
| − | Рассмотрим каждое слагаемое в данной формуле:<br> | + | База утверждения <tex>P_{i,i} = 0, \forall i \in N</tex>; <tex>P_{i,0} = 0, \forall i \in N, i \neq 1 </tex><br> |
| + | Рассмотрим каждое слагаемое в данной формуле <tex>P_{m,k} = k\cdot P_{m-1,k}+(m-k))\cdot P_{m-1,k-1}</tex> :<br> | ||
1) <tex>k\cdot P_{m-1,k}</tex> обозначает, что мы можем подвесить ещё одну вершину к любому из <tex>k</tex> листьев. Тогда количество листьев не изменится, а количество вершин увеличится на одну.<br> | 1) <tex>k\cdot P_{m-1,k}</tex> обозначает, что мы можем подвесить ещё одну вершину к любому из <tex>k</tex> листьев. Тогда количество листьев не изменится, а количество вершин увеличится на одну.<br> | ||
2) <tex>(m-k)\cdot P_{m-1,k-1}</tex> обозначает, что мы можем подвесить ещё одну вершину к любой вершине, не являющийся листом. Таких вершин <tex>(m-k)</tex>. Тогда количество листьев и количество вершин увеличится на один.<br> | 2) <tex>(m-k)\cdot P_{m-1,k-1}</tex> обозначает, что мы можем подвесить ещё одну вершину к любой вершине, не являющийся листом. Таких вершин <tex>(m-k)</tex>. Тогда количество листьев и количество вершин увеличится на один.<br> | ||
Так как мы рассмотрели все возможные варианты присоединения новой вершины, то данная формула <tex>P_{m,k} = k\cdot P_{m-1,k}+(m-k)\cdot P_{m-1,k-1}</tex> верна.<br> | Так как мы рассмотрели все возможные варианты присоединения новой вершины, то данная формула <tex>P_{m,k} = k\cdot P_{m-1,k}+(m-k)\cdot P_{m-1,k-1}</tex> верна.<br> | ||
}} | }} | ||
| − | + | Комбинаторное представление можно записать так : <tex>P_{m} = z\times P_{m-1}</tex> , где <tex>P_{i}</tex> - количество деревьев с <tex>i</tex> вершинами, причем <tex>P_{0} = \varepsilon</tex>.<br> | |
| − | |||
Пример <br> | Пример <br> | ||
[[Файл:0List.png|100px]] <tex>m=1</tex> [[Файл:1List.png|100px]] <tex>m=2</tex> [[Файл:2List.png|400px]] <tex>m=3</tex> [[Файл:3List.png|600px]] <tex>m=4</tex> <br> | [[Файл:0List.png|100px]] <tex>m=1</tex> [[Файл:1List.png|100px]] <tex>m=2</tex> [[Файл:2List.png|400px]] <tex>m=3</tex> [[Файл:3List.png|600px]] <tex>m=4</tex> <br> | ||
Текущая версия на 13:27, 24 июня 2020
| Утверждение: |
Число помеченных корневых деревьев с листьями и вершинами, у которых номер предка меньше номера вершины, есть . |
|
База утверждения ; |
Комбинаторное представление можно записать так : , где - количество деревьев с вершинами, причем .
Пример

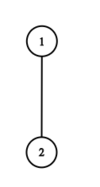
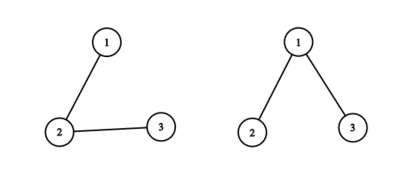
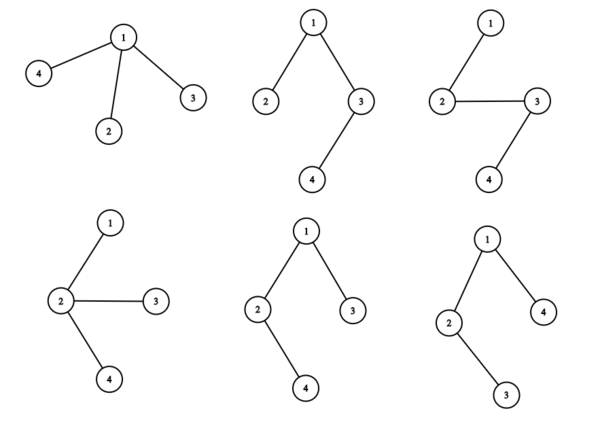
Вершина является корнем.