Блендинг изображений — различия между версиями
Wafemand (обсуждение | вклад) (Почти дописал второй проход, попытался увеличить междустрочный интервал у кода, но безуспешно...) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 71 промежуточная версия 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Копирование элемента одного изображения и его вставка на другое изображение {{---}} один из наиболее используемых методов для создания графического контента. Простая вставка, как правило, бросается в глаза и делает результат похожим на коллаж, во многих случаях этот эффект является нежелательным. | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | '''Блендинг изображений''' (англ. ''image blending'') {{---}} метод, позволяющий вставить часть одного изображения в другое таким образом, чтобы композиция изображений выглядела естественно, без швов на границах вставки. }} | |
| − | + | Основная трудность задачи заключается в том, что естественность результата зависит не только от бесшовности наложения, но и от схожести цветов и текстуры вставляемого и фонового изображений. | |
| − | |||
| − | |||
| − | |||
| − | '''Блендинг изображений''' (англ. ''image blending'') {{---}} метод, позволяющий вставить часть одного изображения в другое таким образом, чтобы композиция изображений выглядела естественно, без швов на границах вставки | ||
| − | |||
| + | {| | ||
| + | ! Вставляемое изображение | ||
| + | ! Фоновое изображение | ||
| + | ! Простая вставка | ||
| + | ! Желаемый результат | ||
| + | |- | ||
| + | | [[Файл:Diver bl diver.png|180px]] | ||
| + | | [[Файл:Diver bl sea.png|180px]] | ||
| + | | [[Файл:Diver bl2.png|180px]] | ||
| + | | [[Файл:Diver bl3.png|180px]] | ||
| + | |} | ||
==Блендинг Пуассона== | ==Блендинг Пуассона== | ||
| − | + | [[Файл:Poisson int1.png|thumb|right|250px|Рисунок $1.1$: Пример перепада яркости при простой вставке<ref name='ZWS20'/>]] | |
| + | [[Файл:Poisson int2.png|thumb|right|250px|Рисунок $1.2$: Результат применения блендинга Пуассона<ref name='ZWS20'/>]] | ||
| − | Простая вставка одного изображения поверх другого нередко влечет заметный перепад яркости на границе вставки. Метод Пуассона заключается в сглаживании этого перепада с целью сделать дефект менее заметным, используя градиент вставляемого изображения и значения пикселей фонового изображения на границе вставки. | + | Простая вставка одного изображения поверх другого нередко влечет заметный перепад яркости на границе вставки (рисунок $1.1$). Метод Пуассона заключается в сглаживании этого перепада (рисунок $1.2$) с целью сделать дефект менее заметным, используя градиент вставляемого изображения и значения пикселей фонового изображения на границе вставки. |
| − | + | '''Замечание:''' Для RGB изображений задача минимизации решается для каждого цветового канала отдельно. | |
| − | Давайте обозначим за $ | + | Давайте обозначим за $S$ изображение, которое служит фоном, а за $I$ {{---}} изображение, вставляемое поверх $S$. Область вставки будем задавать двоичной маской $M$, содержащей единицы в области наложения. Например: |
| + | {| class="wikitable" style="background-color:#FFF; text-align:center" | ||
| + | |- | ||
| + | ! Фоновое <br/> изображение $S$ | ||
| + | ! Накладываемое <br/> изображение $I$ | ||
| + | ! Маска $M$ | ||
| + | |- | ||
| + | | [[Файл:Poisson_cat.jpg|155px]] | ||
| + | | [[Файл:Poisson_cherry.jpg|155px]] | ||
| + | | [[Файл:Poisson_cherry_mask.png|155px]] | ||
| + | |} | ||
| − | Пусть $ | + | === Идея подхода === |
| + | Пусть замкнутое множество $P \subset \mathbb{R}^2$ {{---}} область, на которой определено изображение $S$, а замкнутое множество $\Omega \subset P$ с границей $\partial\Omega$ и внутренностью $int(\Omega)$ {{---}} область вставки изображения $I$. | ||
| − | Пусть $ | + | Пусть $f_S$ {{---}} скалярная функция, определенная на $P \setminus int(\Omega)$, задает фоновое изображение $S$; $f$ {{---}} неизвестная скалярная функция, определенная на $int(\Omega)$, задает, каким образом должно выглядеть результат блендинга в области вставки. |
| − | + | $v_I$ {{---}} векторное поле, определенное на $\Omega$. В качестве $v_I$ возьмем градиент вставляемого изображения $I$: $v_I = \nabla f_I$. | |
| − | $\underset{ | + | Нашей задачей является поиск такой функции $f$, чтобы блендинговое изображение выглядело реалистично. Для этого минимизируем разность градиента функции $f$ и векторного поля $v_I$, считая, что $f = f_S$ на границе $\Omega$. |
| + | $$ | ||
| + | \underset{f}{\mathrm{min}} \underset{\Omega}{\iint} |\nabla f - v_I|^2, \text{где } f|_{\partial \Omega} = f_S|_{\partial \Omega}. | ||
| + | $$ | ||
| + | Решение задачи минимизации является единственным решением уравнения Пуассона для граничных условий Дирихле. | ||
| + | $$\nabla^2 f = \nabla^2 f_I \text{ на } \Omega, f|_{\partial \Omega} = f_S|_{\partial \Omega}, \text{где } \nabla^2 \text{{{---}} оператор Лапласа.}$$ | ||
| − | + | === Дискретный случай === | |
| + | Пусть $p$ {{---}} координаты $(x, y)$ пикселя двухмерного изображения. За $Img_p$ обозначим значение пикселя с координатами $p$ изображения $Img$. Пусть $\Omega = \left\{ p\;|\;M_p = 1 \right\}$ {{---}} область, заданная маской $M$. Тогда $\partial \Omega$ {{---}} координаты границы вставляемой области, а $int(\Omega)$ {{---}} внутренность области. | ||
| − | + | Пусть $N_p$ {{---}} множество соседей $p$ (максимум четыре пикселя, имеющих общую границу с $p$, т.е. пиксели со следующими координатами: $(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)$). Для всех пар $(p, q)$ таких, что $q \in N_p$, введем $v_{pq} = I_p - I_q$. | |
| − | + | Введем переменные $O_p, p \in \Omega$. Так как мы хотим сделать результат бесшовным, пиксели $O_p, p \in \partial\Omega$, сделаем равными $S_p$. Для $p, q \in int(\Omega),\; q \in N_p$ постараемся найти такое $O$, чтобы разность $O_p$ и $O_q$ была близка к $v_{pq}$. Для этого решим задачу минимизации: | |
| − | + | $$ | |
| + | \underset{O_p,\; p \in \Omega}{\mathrm{min}}\; \underset{p, q \in \Omega}{\sum}\; \left(O_p - O_q - v_{pq}\right)^2, \text{где } O_p = S_p, p \in \partial \Omega. | ||
| + | $$ | ||
| − | + | Заметим, что функция, которую мы хотим минимизировать, квадратична относительно переменных $O_p, p \in int(\Omega)$. Для решения задачи минимизации вычислим частные производные по этим переменным и найдем значения переменных, при которых частные производные будут равны нулю. | |
| − | + | $$\frac{\partial{\underset{p, q \in \Omega}{\sum}\; \left(O_p - O_q - v_{pq}\right)^2}}{\partial O_p} = \underset{q \in N_p}{\sum} 2 \left(O_p - O_q - v_{pq}\right) - \underset{q \in N_p}{\sum} 2 \left(O_q - O_p - v_{qp}\right) = 2 \underset{q \in N_p}{\sum} 2 \left(O_p - O_q - v_{pq}\right).$$ | |
| − | |||
| − | |||
| − | |||
| + | Приравнивая к нулю, получаем: $|N_p| O_p - \underset{q \in N_p}{\sum} O_q = \underset{q \in N_p}{\sum} v_{pq}$. | ||
| − | + | Добавим условие $O_p = S_p, p \in \partial \Omega$: $\;|N_p| O_p - \underset{q \in N_p \cap int(\Omega)}{\sum} O_q = \underset{q \in N_p \cap \partial \Omega}{\sum} S_q + \underset{q \in N_p}{\sum} v_{pq}$. | |
| − | https:// | + | Для решения систем уравнений такого вида могут быть использованы итеративные алгоритмы Gauss-Seidel и V-cycle multigrid<ref name="PGB03">[https://www.cs.jhu.edu/~misha/Fall07/Papers/Perez03.pdf Poisson Image Editing] Patrick Perez, Michel Gangnet, Andrew Blake (2003)</ref>. |
| − | + | Получаем значения пикселей $O_p$, $p \in int(\Omega)$. Тогда результат $B$ блендинга Пуассона будет следующим: | |
| + | $$ | ||
| + | B_p = | ||
| + | \begin{cases} | ||
| + | O_p,\; \text{если } p \in int(\Omega) \\ | ||
| + | S_p,\; \text{иначе } | ||
| + | \end{cases}. | ||
| + | $$ | ||
| − | = | + | Mетод Пуассона сдвигает цвета накладываемого изображения, сохраняя свойства градиента (т.е. если пиксель $I_{p1}$ был меньше $I_{p2}$, то после преобразования $I_{p1}$ не станет больше $I_{p2}$), однако само значение градиета может получиться другим.<ref name='clear_poisson'>https://erkaman.github.io/posts/poisson_blending.html Poisson blending для самых маленьких</ref> |
| − | Прежде чем переходить к гармонизации картин, рассмотрим задачу | + | ==Нейронный перенос стиля== |
| + | {{main|Neural Style Transfer}} | ||
| + | Прежде чем переходить к гармонизации картин, рассмотрим задачу нейронного переноса стиля с изображения $S$ на изображение $I$. Для этого используются выходы скрытых слоёв [[Сверточные нейронные сети | свёрточной нейронной сети]] VGG-19<ref name="SZ14">[https://arxiv.org/pdf/1409.1556.pdf Very Deep Convolutional Networks for Large-Scale Image Recognition] Karen Simonyan, Andrew Zisserman (2014)</ref> (конкретные слои указаны ниже в деталях реализации). | ||
| − | Основная идея генерации изображения {{---}} решение оптимизационной задачи $\mathcal{L}( | + | Основная идея генерации изображения {{---}} решение оптимизационной задачи $\mathcal{L}(I, S, O) \xrightarrow[O]{} min$, где $O$ {{---}} итоговое изображение, $\mathcal{L}(I, S, O)$ {{---}} [[Функция потерь и эмпирический риск | функция потерь]]. Такую задачу можно решать градиентным спуском в пространстве изображений используя [[обратное распространение ошибки | метод обратного распространения ошибки]]. |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Пусть $F^l\left[I\right] \in \mathcal{R}^{N_l \times M_l}$ {{---}} | + | Пусть $F^l\left[I\right] \in \mathcal{R}^{N_l \times M_l}$ {{---}} матрица значений выхода $l$-го слоя сети на изображении $I$. Выход $l$-го слоя сети имеет размерность $N_l \times W_l \times H_l$. Представим его как матрицу $N_l \times M_l$, где $N_l$ {{---}} количество фильтров в $l$-ом слое, $M_l$ {{---}} количество признаков ($M_l = W_l H_l$). Тогда $F^l_{ij}\left[I\right]$ {{---}} $j$-ый признак $i$-го фильтра в $l$-ом слое. Столбец матрицы $F^l\left[I\right]$ размера $N_l$ назовём '''вектором активации'''.}} |
| − | где $N_l$ {{---}} количество фильтров в $l$-ом слое, | ||
| − | $M_l$ {{---}} количество признаков ( | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Матрица Грама''' (англ. ''Gram matrix'') {{---}} матрица попарных скалярных произведений. | + | '''Матрица Грама''' (англ. ''Gram matrix'') {{---}} матрица попарных скалярных произведений. |
| + | $$G^l\left[S\right] \in \mathcal{R}^{N_l \times N_l},$$ | ||
| + | $$G^l\left[S\right] = F^l\left[S\right]F^l\left[S\right]^T.$$}} | ||
| − | + | Далее рассмотренны функции потерь, которые мы будем использовать. | |
| − | + | ===Content loss=== | |
| − | + | ||
| − | $ | + | $F^l\left[I\right]$ отражает содержание изображения. Мы хотим чтобы содержание результата было как можно ближе к исходной картинке. Введём для этого такую функцию потерь: |
| − | $ | + | $$\mathcal{L}_{content}(I, O) = \displaystyle\sum_l \frac{\alpha_l}{2 N_l M_l}\displaystyle\sum_{i, j} \left(F^l_{ij}\left[I\right] - F^l_{ij}\left[O\right]\right)^2,$$ |
| − | + | где $\alpha_l$ {{---}} вклад $l$-го слоя в функцию потерь. | |
| − | |||
| − | $\mathcal{L | ||
| − | $\ | ||
| − | + | ===Style loss=== | |
| − | + | $G^l\left[S\right]$ отражает статистику выходов фильтров независимо от их расположения, что, в свою очередь, отражает стиль изображения. Чтобы стиль результата был похож на стилевое изображение, введём следующую функцию потерь: | |
| − | + | $$\mathcal{L}_{style}(S, O) = \displaystyle\sum_l \frac{\beta_l}{2N_l^2} \displaystyle\sum_{i, j} \left(G^l_{ij}\left[S\right] - G^l_{ij}\left[O\right]\right)^2,$$ | |
| − | + | где $\beta_l$ {{---}} вклад $l$-го слоя в функцию потерь. | |
| − | + | ===Gatys' loss=== | |
| − | + | Скомбинируем $\mathcal{L}_{content}$ и $\mathcal{L}_{style}$ и получим функцию потерь, которая была использована в алгоритме Гатиса<ref name="GEB16">[https://rn-unison.github.io/articulos/style_transfer.pdf Image Style Transfer Using Convolutional Neural Networks] Leon A. Gatys, Alexander S. Ecker, Matthias Bethge (2016)</ref>: | |
| + | $$\mathcal{L}_{Gatys}(I, S, O) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{style}(S, O).$$ | ||
| + | Вес $w_{style}$, векторы $\alpha$ и $\beta$ являются, в некотором смысле, гиперпараметрами алгоритма, которые мы выберем позднее. | ||
===Histogram Loss=== | ===Histogram Loss=== | ||
| − | Авторы другой статьи<ref name="WRB17">[https://arxiv.org/pdf/1701.08893.pdf Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses] Eric Risser, Pierre Wilmot, Connelly Barnes (2017)</ref> показывают, что результаты, полученные с помощью $\mathcal{L}_{Gatys}$ нестабильны и предложили | + | Авторы другой статьи<ref name="WRB17">[https://arxiv.org/pdf/1701.08893.pdf Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses] Eric Risser, Pierre Wilmot, Connelly Barnes (2017)</ref> показывают, что результаты, полученные с помощью $\mathcal{L}_{Gatys}$ нестабильны и предложили учитывать ещё одну функцию потерь, основанную на '''сопоставлении гистограмм'''. |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
'''Сопоставление гистограмм''' (англ. ''Histogram matching'') {{---}} метод обработки изображения, после которого гистограмма изображения совпадает с целевой гистограммой<ref name="HistMatch">https://en.wikipedia.org/wiki/Histogram_matching</ref>.}} | '''Сопоставление гистограмм''' (англ. ''Histogram matching'') {{---}} метод обработки изображения, после которого гистограмма изображения совпадает с целевой гистограммой<ref name="HistMatch">https://en.wikipedia.org/wiki/Histogram_matching</ref>.}} | ||
| − | + | Пусть $R = histmatch(S, O)$ {{---}} отображение пикселей такое, что гистограмма $S$ совпадает с гистограммой $R(O)$, тогда Histogram loss будет выглядеть так: | |
| − | + | $$\mathcal{L}_{hist}(S, O) = \displaystyle\sum_l \gamma_l \displaystyle\sum_{i, j} \left(F^l_{ij}\left[O\right] - R\left(F^l_{ij}\left[O\right]\right)\right)^2,$$ | |
| − | Пусть $R = histmatch(S, O)$ {{---}} отображение пикселей такое, что гистограмма $S$ совпадает с гистограммой $R(O)$ | + | где $\gamma_l$ {{---}} вклад $l$-го слоя в функцию потерь. |
| − | + | ||
| − | + | '''Замечание:''' Если в случае остальных функций потерь нетрудно посчитать производную, то здесь могут возникнуть проблемы. Но поскольку $\displaystyle\frac{\partial \mathcal{L}_{hist}}{\partial F^l_{ij}\left[O\right]}$ является нулём почти везде, авторы предлагают при подсчёте производной считать $R\left(F^l_{ij}\left[O\right]\right)$ константой, которая не зависит от $O$. | |
| − | $\mathcal{L | ||
| − | $\gamma_l$ {{---}} вклад $l$-го слоя в функцию потерь}} | ||
===Total variation loss=== | ===Total variation loss=== | ||
| − | Также добавим ещё одну функцию потерь, которая | + | Также добавим ещё одну функцию потерь, которая удаляет шумы, при этом сохраняя важные детали изображения<ref name="MV15">[https://arxiv.org/pdf/1412.0035.pdf Understanding Deep Image Representations by Inverting Them] Aravindh Mahendran, Andrea Vedaldi (2015)</ref><ref name="JAFF16">[https://arxiv.org/pdf/1603.08155.pdf Perceptual Losses for Real-Time Style Transfer and Super-Resolution] Justin Johnson, Alexandre Alahi, Li Fei-Fei (2016)</ref>: |
| − | + | ||
| − | + | $$\mathcal{L}_{tv}(O) = \displaystyle\sum_{i, j} \left(O^l_{i, j} - O^l_{i-1, j}\right)^2 + \left(O^l_{i, j} - O^l_{i, j-1}\right)^2.$$ | |
| − | $\mathcal{L}_{tv}(O) = \displaystyle\sum_{i, j} (O^l_{i, j} - O^l_{i-1, j} | ||
==Глубокая гармонизация картин== | ==Глубокая гармонизация картин== | ||
| − | Для того чтобы вставить изображение в картину или рисунок нужно не только сделать бесшовный переход и изменить цвета, но ещё и изменить текстуру вставляемого изображения, например сымитировать мазки кистью. Используем для этого комбинацию подходов из других статей<ref name="GEB16"/><ref name="JAFF16"/><ref name="WRB17"/>. | + | Для того чтобы вставить изображение в картину или рисунок нужно не только сделать бесшовный переход и изменить цвета, но ещё и изменить текстуру вставляемого изображения, например, сымитировать мазки кистью (рисунок $2$). Используем для этого комбинацию подходов из других статей<ref name="GEB16"/><ref name="JAFF16"/><ref name="WRB17"/>. |
| − | Алгоритм | + | <div class="oo-ui-panelLayout-scrollable" style="display: block; vertical-align:middle; height: auto; max-width: auto; float: center">[[Файл:LPSB18_Figure_1.png|750px|thumb|center|Рисунок $2$: Пример работы алгоритма ''Deep Image Analogy''<ref name="LYY*17">[https://arxiv.org/pdf/1705.01088.pdf Visual Attribute Transfer through Deep Image Analogy] Jing Liao, Yuan Yao, Lu Yuan, Gang Hua, Sing Bing Kang (2017)</ref> ($3$ картинка) и ''Deep Painterly Harmonization''<ref name="LPSB18"/> ($4$ картинка)]]</div> |
| + | Алгоритм состоит из двух проходов. Первый проход делает грубую гармонизацию, а второй {{---}} более тщательную. Отличаются они '''стилевым маппингом''' и функциями потерь<ref name="LPSB18">https://arxiv.org/pdf/1804.03189.pdf Fujun Luan, Sylvain Paris, Eli Shechtman, Kavita Bala (2018)</ref>. | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | '''Стилевым маппингом''' | + | '''Стилевым маппингом''' назовём отображение $P : \mathcal{R}^{N_l \times M_l} \rightarrow \mathcal{R}^{N_l \times M_l}$, которое некоторым образом переставляет столбцы матрицы (не обязательно обратимо, то есть столбцы могут теряться и копироваться). Более формально, пусть $p(j)$ {{---}} новая позиция столбца $j$, тогда $P(Q)_{i, p(j)} = Q_{ij}$.}} |
| − | Один проход | + | Один проход состоит из $3$ частей: |
# Входное $I$ и стилевое $S$ изображения подаются на вход нейронной сети VGG-19, так мы получаем $F^l_{ij}\left[I\right]$ и $F^l_{ij}\left[S\right]$. | # Входное $I$ и стилевое $S$ изображения подаются на вход нейронной сети VGG-19, так мы получаем $F^l_{ij}\left[I\right]$ и $F^l_{ij}\left[S\right]$. | ||
| − | # Для каждого слоя $l$ некоторым алгоритмом cтроится стилевой маппинг $P_l$, который сопоставляет столбцам из $F_l[I]$ столбцы из $F_l[S]$. | + | # Для каждого слоя $l$ некоторым алгоритмом $\pi$ cтроится стилевой маппинг $P_l$, который сопоставляет столбцам из $F_l[I]$ столбцы из $F_l[S]$. |
| − | # Изображение $O$ восстанавливается градиентным спуском по пространству изображений | + | # Изображение $O$ восстанавливается градиентным спуском по пространству изображений с использованием функции потерь $\mathcal{L}$. |
<font size="3em"> | <font size="3em"> | ||
'''fun''' $SinglePassHarmonization$( | '''fun''' $SinglePassHarmonization$( | ||
| − | $I$, <font color="green"> | + | <span style="display: inline-block; width: 3em">$I$,</span><font color="green">// Входное изображение </font> |
| − | $M$, <font color="green"> | + | <span style="display: inline-block; width: 3em">$M$,</span><font color="green">// Маска </font> |
| − | $S$, <font color="green"> | + | <span style="display: inline-block; width: 3em">$S$,</span><font color="green">// Стилевое изображение </font> |
| − | $\pi$, <font color="green"> | + | <span style="display: inline-block; width: 3em">$\pi$,</span><font color="green">// Алгоритм построения стилевого маппинга </font> |
| − | $\mathcal{L}$ <font color="green"> | + | <span style="display: inline-block; width: 3em">$\mathcal{L}$</span><font color="green">// Функция потерь </font> |
): | ): | ||
<font color="green">// Строим матрицы $F[I]$ и $F[S]$ с помощью свёрточной сети VGG-19 </font> | <font color="green">// Строим матрицы $F[I]$ и $F[S]$ с помощью свёрточной сети VGG-19 </font> | ||
| Строка 133: | Строка 164: | ||
<font color="green">// Градиентным спуском ищем изображение $O$, которое минимизирует $\mathcal{L}$ </font> | <font color="green">// Градиентным спуском ищем изображение $O$, которое минимизирует $\mathcal{L}$ </font> | ||
$O \leftarrow Reconstruct(I, M, S, P, \mathcal{L})$ | $O \leftarrow Reconstruct(I, M, S, P, \mathcal{L})$ | ||
| − | |||
'''return''' $O$ | '''return''' $O$ | ||
</font> | </font> | ||
===Первый проход=== | ===Первый проход=== | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | ''' | + | '''Патчем''' (англ. ''patch'') для столбца $j$ будем называть тензор $3 \times 3 \times N_l$, который состоит из соседних векторов активации в тензоре выхода свёрточного слоя, с центром в $(x, y)$, где $j = y W_l + x$.}} |
| − | |||
| − | |||
| − | |||
| − | Первый проход делает грубую гармонизацию, но при этом он хорошо работает с любыми стилями. Здесь используется алгоритм | + | <div class="tright" style="clear:none">[[Файл:LPSB18_Figure_2c.png|250px|thumb|none|Рисунок $3.2$: Результаты после второго прохода<ref name="WRB17"/>]]</div> |
| + | <div class="tright" style="clear:none">[[Файл:LPSB18_Figure_2b.png|250px|thumb|none|Рисунок $3.1$: Результаты после первого прохода<ref name="WRB17"/>]]</div> | ||
| + | |||
| + | Первый проход делает грубую гармонизацию, но при этом он хорошо работает с любыми стилями (рисунок $3.1$). Здесь используется алгоритм $IndependentMapping$ для построения стилевого маппинга. Этот алгоритм для каждого столбца $j$ в $F_l[I]$ ищет столбец $p(j)$ в $F_l[S]$, такой что евклидово расстояние между патчем $F_l[I]$ с центром $j$ и патчем $F_l[S]$ с центром $p(j)$ минимально (метод ближайшего соседа). | ||
<font size="3em"> | <font size="3em"> | ||
'''fun''' $IndependentMapping$( | '''fun''' $IndependentMapping$( | ||
| − | $F[I]$, <font color="green"> | + | <span style="display: inline-block; width: 5em">$F[I]$,</span><font color="green">// Выходы слоёв после входного изображения </font> |
| − | $Mask$, <font color="green"> | + | <span style="display: inline-block; width: 5em">$Mask$,</span><font color="green">// Маска </font> |
| − | $F[S]$ <font color="green"> | + | <span style="display: inline-block; width: 5em">$F[S]$</span><font color="green">// Выходы слоёв после стилевого изображения </font> |
): | ): | ||
| − | '''for''' $l \in [1 : L]$: <font color="green"> // | + | <font color="green">// Для всех слоёв от $1$ до $L$ </font> |
| + | '''for''' $l \in [1 : L]$: | ||
| + | <font color="green">// Для всех столбцов от $1$ до $M_l$ </font> | ||
'''for''' $j \in [1 : M_l]$: | '''for''' $j \in [1 : M_l]$: | ||
| − | '''if''' $j \in Resize(Mask, l)$: <font color="green"> // | + | <font color="green">// Рассматриваем патчи только внутри маски, которую нужно масштабировать в соответсвии с размером слоя $l$ </font> |
| − | $ | + | '''if''' $j \in Resize(Mask, l)$: |
| − | + | <font color="green">// Берём самый похожий стилевой патч и записываем его в маппинг. </font> | |
| + | $P_l(j) \leftarrow NearestNeighborIndex(F[I], j, F[S])$ | ||
'''return''' $P$ | '''return''' $P$ | ||
</font> | </font> | ||
| − | В первом проходе используется модифицированная функция потерь $\mathcal{L}_{Gatys}$, с тем лишь отличием, что к $F_l[S]$ применяется стилевой маппинг $P_l$ | + | В первом проходе используется модифицированная функция потерь $\mathcal{L}_{Gatys}$, с тем лишь отличием, что в $\mathcal{L}_{style}$ к $F_l[S]$ применяется стилевой маппинг $P_l$: |
| − | + | ||
| − | + | $$\mathcal{L}_1(I, S, O, P) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{style}(S, O, P).$$ | |
| − | $\mathcal{L}_1(I, S, O, P) = \mathcal{L | ||
| − | + | '''Замечание:''' при посчёте градиента $\mathcal{L}_{content}$ используются только пиксели внутри маски<ref>https://github.com/luanfujun/deep-painterly-harmonization/blob/a33a9a70366b6baff1cc0291f857b5895b271fc1/neural_gram.lua#L349</ref>. | |
===Второй проход=== | ===Второй проход=== | ||
| − | |||
| − | |||
| − | </ | + | [[Файл:LPSB18_Figure_5c.png|thumb|right|250px|Рисунок $4.1$: Только первый проход<ref name="WRB17"/>]] |
| + | [[Файл:LPSB18_Figure_5d.png|thumb|right|250px|Рисунок $4.2$: Только второй проход<ref name="WRB17"/>]] | ||
| + | [[Файл:LPSB18_Figure_5f.png|thumb|right|250px|Рисунок $4.3$: Результат с $\mathcal{L}_{style}$ вместо $\mathcal{L}_{s1}$<ref name="WRB17"/>]] | ||
| + | [[Файл:LPSB18_Figure_5g.png|thumb|right|250px|Рисунок $4.4$: Оба прохода<ref name="WRB17"/>]] | ||
| + | [[Файл:LPSB18_Figure_5h.png|thumb|right|250px|Рисунок $4.5$: Финальный результат<ref name="WRB17"/>]] | ||
| − | + | Второй проход делает более качественную гармонизацию после первого прохода (рисунок $3.2$). Здесь мы будем использовать более сложный алгоритм $ConsistentMapping$ построения стилевого маппинга и более сложную функцию потерь. Суть этого алгоритма в том, чтобы найти стилевой мапинг на некотором слое $l_{ref}$ и перенести этот маппинг на остальные слои. Также, мы будем предпочитать маппинги, в которых смежные патчи в $F_l[S]$ остаются смежными после мапинга, чтобы обеспечить пространсвенную согласованность (таким образом мы хотим переносить сложные текстуры более качественно, например, мазки кистью). Если применять второй проход сразу, то результаты получаются хуже (рисунок $4.2$). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <font size="3em"> | |
| − | ''' | + | '''fun''' $ConsistentMapping$( |
| − | + | <span style="display: inline-block; width: 5em">$F[I]$,</span><font color="green">// Выходы слоёв после входного изображения </font> | |
| − | + | <span style="display: inline-block; width: 5em">$Mask$,</span><font color="green">// Маска </font> | |
| − | + | <span style="display: inline-block; width: 5em">$F[S]$</span><font color="green">// Выходы слоёв после стилевого изображения </font> | |
| − | + | ): | |
| − | + | <font color="green">// Сначала посчитаем маппинг как в IndependentMapping только для слоя $l_{ref}$ </font> | |
| − | + | '''for''' $j \in [1 : M_{l_{ref}}]$: | |
| + | '''if''' $j \in Resize(Mask, l_{ref})$: | ||
| + | $P_0(j) \leftarrow NearestNeighborIndex(F[I], j, F[S])$ | ||
| − | + | <font color="green">// Далее обеспечиваем пространсвенную согласованность </font> | |
| − | + | '''for''' $j \in [1 : M_{l_{ref}}]$: | |
| − | </ | + | '''if''' $j \in Resize(Mask, l_{ref})$: |
| + | $q \leftarrow P_0(j)$ | ||
| + | <font color="green">// Инициализируем множество кандидатов на новый маппинг </font> | ||
| + | $CSet \leftarrow \{q\}$ | ||
| + | <font color="green">// Перебираем все смежные патчи </font> | ||
| + | '''for''' $o \in \left\{N, NE, E, SE, S, SW, W, NW\right\}$: | ||
| + | <font color="green">// Добавляем в кандидаты патч, сосед которого является маппингом для нашего соседа в соответсвующем направлении </font> | ||
| + | $CSet \leftarrow CSet \cup \left\{P_0(j + o) - o\right\}$ | ||
| + | <font color="green">// Среди всех кандидатов выбираем тот, который ближе всего к маппингам наших соседей </font> | ||
| + | $P_{l_{ref}}(j) \leftarrow \underset{c \in CSet}{\mathrm{argmin}}\displaystyle\sum_o \left\|(F_{l_{ref}}[S]_c - F_{l_{ref}}[S]_{P_0(j + o)}\right\|^2$ | ||
| + | |||
| + | <font color="green">// Теперь нужно перенести маппинг для $l_{ref}$ на остальные слои </font> | ||
| + | '''for''' $l \in [1 : L] \setminus \{l_{ref}\}$: | ||
| + | '''for''' $j \in [1 : M_l]$: | ||
| + | '''if''' $j \in Resize(Mask, l)$: | ||
| + | <font color="green">// Вычисляем позицию $j'$ на слое $l_{ref}$ соответствующую позиции $j$ на слое $l$</font> | ||
| + | $j' \leftarrow ChangeResolution(l, l_{ref}, j)$ | ||
| + | <font color="green">// Берём маппинг для позиции $j'$</font> | ||
| + | $q \leftarrow P_{l_{ref}}(j')$ | ||
| + | <font color="green">// Переносим позицию $q$ обратно на слой $l$</font> | ||
| + | $P_l(j) \leftarrow ChangeResolution(l_{ref}, l, q)$ | ||
| + | '''return''' $P$ | ||
| + | </font> | ||
| + | |||
| + | При вычислении стилевого маппинга появляется очень много дублирующихся векторов, что даёт не очень хорошие результаты (рисунок $4.3$). Поэтому при вычислении матрицы Грама выкинем повторяющиеся векторы. Назовём функцию потерь с такой модификацией $\mathcal{L}_{s1}$. | ||
| + | |||
| + | $$\mathcal{L}_2(I, S, O, P) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{s1}(S, O, P) + w_{hist}\mathcal{L}_{hist}(S, O) + w_{tv}\mathcal{L}_{tv}(O),$$ | ||
| + | где $w_{style}, w_{hist}, w_{tv}$ {{---}} веса соответсвующих функций потерь. | ||
| − | { | + | <!-- |
| − | | | + | {| class="wikitable" style="background-color:#FFF; text-align:center" |
| − | $ | + | |- |
| + | | Рисунок $4.1$: Только первый проход<ref name="WRB17"/> | ||
| + | | Рисунок $4.2$: Только второй проход<ref name="WRB17"/> | ||
| + | | Рисунок $4.3$: Результат с $\mathcal{L}_{style}$ вместо $\mathcal{L}_{s1}$<ref name="WRB17"/> | ||
| + | | Рисунок $4.4$: Оба прохода<ref name="WRB17"/> | ||
| + | | Рисунок $4.5$: Финальный результат<ref name="WRB17"/> | ||
| + | |- | ||
| + | | [[Файл:LPSB18_Figure_5c.png|250px]] | ||
| + | | [[Файл:LPSB18_Figure_5d.png|250px]] | ||
| + | | [[Файл:LPSB18_Figure_5f.png|250px]] | ||
| + | | [[Файл:LPSB18_Figure_5g.png|250px]] | ||
| + | | [[Файл:LPSB18_Figure_5h.png|250px]] | ||
| + | |} | ||
| + | --> | ||
===Итоговый алгоритм=== | ===Итоговый алгоритм=== | ||
| + | |||
| + | Теперь осталось запустить две стадии: | ||
<font size="3em"> | <font size="3em"> | ||
| − | '''fun''' Harmonization( | + | '''fun''' $Harmonization$( |
| − | I, <font color="green"> | + | <span style="display: inline-block; width: 5em">$I$,</span><font color="green">// Входное изображение </font> |
| − | Mask, <font color="green"> | + | <span style="display: inline-block; width: 5em">$Mask$,</span><font color="green">// Маска </font> |
| − | S | + | <span style="display: inline-block; width: 5em">$S$</span><font color="green">// Стилевое изображение </font> |
): | ): | ||
<font color="green">// Грубый проход алгоритма. Каждый слой рассматривается отдельно при построении стилевого маппинга. </font> | <font color="green">// Грубый проход алгоритма. Каждый слой рассматривается отдельно при построении стилевого маппинга. </font> | ||
| − | I' | + | $I' \leftarrow SinglePassHarmonization(I, Mask, S, IndependentMapping, \mathcal{L}_1)$ |
<font color="green">// Улучшение результата. Стилевой маппинг строится консистентно для всех слоёв. </font> | <font color="green">// Улучшение результата. Стилевой маппинг строится консистентно для всех слоёв. </font> | ||
| − | O | + | $O \leftarrow SinglePassHarmonization(I', Mask, S, ConsistentMapping, \mathcal{L}_2)$ |
| − | '''return''' O | + | '''return''' $O$ |
</font> | </font> | ||
| − | * | + | ===Постобработка=== |
| − | * | + | |
| + | [[Файл:LPSB18_Figure_6abc.png|400px|thumb|right|Рисунок $5$: Результат постобработки (без постобработки, после первой стадии, после второй стадии)<ref name="WRB17"/>]] | ||
| + | |||
| + | Описанный алгоритм даёт хорошие результаты в целом, но при ближайшем рассмотрении могут быть артефакты (рисунок $5$). Поэтому сделаем двухступенчатую постобработку (подробное описание есть в оригинальной статье<ref name="LPSB18"/>): | ||
| + | # Переведём изображение в цветовое пространство [https://en.wikipedia.org/wiki/CIELAB_color_space $L*\alpha*\beta$] и применим [https://en.wikipedia.org/wiki/Guided_filter Guided filter] для a и b каналов. | ||
| + | # С помощью алгоритма PatchMatch<ref name="BSFG09">https://www.researchgate.net/profile/Eli_Shechtman/publication/220184392_PatchMatch_A_Randomized_Correspondence_Algorithm_for_Structural_Image_Editing/links/02e7e520897b12bf0f000000.pdf Connelly Barnes, Eli Shechtman, Adam Finkelstein, Dan B Goldman (2009)</ref> и того же Guided filter делаем так, чтобы все патчи выходного изображения присутсвовали в стилевом (чтобы не было новых объектов или структур). | ||
| + | |||
| + | ===Детали реализации=== | ||
| + | |||
| + | [[Файл:LPSB18_Figure_4.png|400px|thumb|right|Рисунок $6$: Влияние $l_{ref}$ на результат<ref name="WRB17"/>]] | ||
| + | |||
| + | Возьмём $l_{ref}$ = conv4_1 (что будет если использовать другие слои видно на рисунке $6$). | ||
| + | Выберем следующие веса для слоёв: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Первый проход | ||
| + | |- | ||
| + | ! Параметр | ||
| + | ! conv1_1 | ||
| + | ! conv2_1 | ||
| + | ! conv3_1 | ||
| + | ! conv4_1 | ||
| + | ! conv5_1 | ||
| + | |- | ||
| + | ! $\alpha$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $1$ | ||
| + | | $0$ | ||
| + | |- | ||
| + | ! $\beta$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $1/3$ | ||
| + | | $1/3$ | ||
| + | | $1/3$ | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Второй проход | ||
| + | |- | ||
| + | ! Параметр | ||
| + | ! conv1_1 | ||
| + | ! conv2_1 | ||
| + | ! conv3_1 | ||
| + | ! conv4_1 | ||
| + | ! conv5_1 | ||
| + | |- | ||
| + | ! $\alpha$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $1$ | ||
| + | | $0$ | ||
| + | |- | ||
| + | ! $\beta$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | | $0$ | ||
| + | |- | ||
| + | ! $\gamma$ | ||
| + | | $1/2$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | | $1/2$ | ||
| + | | $0$ | ||
| + | |} | ||
| + | |||
| + | <!-- | ||
| + | {| class="wikitable" | ||
| + | |+ Веса функций потерь | ||
| + | |- | ||
| + | ! $w_{style}$ | ||
| + | ! $w_{hist}$ | ||
| + | ! $w_{tv}$ | ||
| + | |- | ||
| + | | $\tau$ | ||
| + | | $\tau$ | ||
| + | | $\tau\frac{10}{1 + \exp(10^4 * noise(S) - 25)}$ | ||
| + | |} | ||
| + | --> | ||
| + | Введём гиперпараметр $\tau$ и возьмём $w_{style} = w_{hist} = \tau$, $w_{tv} = \tau\frac{10}{1 + \exp(10^4 * noise(S) - 25)}$, где $noise(S) = \underset{i,j}{\mathrm{med}}\left\{\left(O^l_{i, j} - O^l_{i-1, j}\right)^2 + \left(O^l_{i, j} - O^l_{i, j-1}\right)^2\right\}$<ref>[https://github.com/luanfujun/deep-painterly-harmonization/blob/a33a9a70366b6baff1cc0291f857b5895b271fc1/neural_paint.lua#L470 код функции $noise$.</ref>. | ||
| + | |||
| + | Для того чтобы подбирать $\tau$ авторы статьи использовали классификатор стилей изображений. Они взяли VGG-19, обучили её классифицировать $18$ различных стилей. Эти стили были разделены на $3$ категории с разными $\tau$. Используя $Softmax$ можно интерполировать необходимый $\tau$ по следующей таблице: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Категория стиля | ||
| + | ! Примеры стилей | ||
| + | ! $\tau$ | ||
| + | |- | ||
| + | ! Слабый | ||
| + | | Барокко, Высокое Возрождение | ||
| + | | $1$ | ||
| + | |- | ||
| + | ! Средний | ||
| + | | Абстрактное Искусство, Постимпрессионизм | ||
| + | | $5$ | ||
| + | |- | ||
| + | ! Сильный | ||
| + | | Кубизм, Экспрессионизм | ||
| + | | $10$ | ||
| + | |} | ||
| + | |||
| + | На рисунке $4.4$ результат алгоритма без подбора гиперпараметров. Видно, что самолёт ярче, чем остальное изображение. С подбором параметров получается более естественный результат (рисунок $4.5$). | ||
| + | |||
| + | ===Примеры=== | ||
| + | Примеры взяты с [https://github.com/luanfujun/deep-painterly-harmonization/tree/master/results Github авторов]. | ||
| + | |||
| + | {| | ||
| + | ! Исходное изображение | ||
| + | ! Простая вставка | ||
| + | ! Результат | ||
| + | ! Постобработка | ||
| + | |- | ||
| + | | [[Файл:5_target.jpg|180px]] | ||
| + | | [[Файл:5_naive.jpg|180px]] | ||
| + | | [[Файл:5_final_res.png|180px]] | ||
| + | | [[Файл:5_final_res2.png|180px]] | ||
| + | |- | ||
| + | | [[Файл:6_target.jpg|180px]] | ||
| + | | [[Файл:6_naive.jpg|180px]] | ||
| + | | [[Файл:6_final_res.png|180px]] | ||
| + | | [[Файл:6_final_res2.png|180px]] | ||
| + | |- | ||
| + | | [[Файл:10_target.jpg|180px]] | ||
| + | | [[Файл:10_naive.jpg|180px]] | ||
| + | | [[Файл:10_final_res.png|180px]] | ||
| + | | [[Файл:10_final_res2.png|180px]] | ||
| + | |} | ||
| + | |||
| + | ===Более новые подходы=== | ||
| + | |||
| + | * [https://arxiv.org/pdf/2006.00809.pdf Foreground-aware Semantic Representations for Image Harmonization] | ||
| + | * [https://arxiv.org/pdf/2009.09169.pdf BargainNet: Background-Guided Domain Translation for Image Harmonization] | ||
| + | |||
| + | ==Глубокий блендинг== | ||
| + | <!-- Настя лапочка :3 --> | ||
| − | + | Алгоритм глубокого блендинга состоит из двух этапов. На первом этапе на стилевое изображения $S$ бесшовно накладывается входное изображение $I$, получается подготовительное блендинг-изображение $B$. На втором этапе $B$ модифицируется таким образом, чтобы результат по стилю был похож на $S$. | |
| − | '''fun''' | + | Будем считать, что на вход подаются изображения, прошедшие предварительную обработку: |
| − | $I$, <font color="green"> // Входное изображение </font> | + | * Используемая для вставки часть $I$ вырезана с помощью маски. |
| − | $M$, <font color="green"> // Маска </font> | + | * $M$ и $I$ выровнены относительно $S$. |
| − | $S$ | + | * Размеры матриц, задающих $M, S, I$, совпадают. |
| + | |||
| + | '''Примеры входных данных:''' | ||
| + | {| class="wikitable" style="background-color:#FFF; text-align:center" | ||
| + | ! '''Стилевое <br/> изображение $S$'''<ref name='ZWS20'/> | ||
| + | | [[Файл:Deep bl s1.png|150px]] | ||
| + | | [[Файл:Deep bl s2.png|150px]] | ||
| + | | [[Файл:Deep bl s3.png|150px]] | ||
| + | |- | ||
| + | ! '''Накладываемое <br/> изображение $I$'''<ref name='ZWS20'/> | ||
| + | | [[Файл:Deep bl i1.png|150px]] | ||
| + | | [[Файл:Deep bl i2.png|150px]] | ||
| + | | [[Файл:Deep bl i3.png|150px]] | ||
| + | |} | ||
| + | |||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Простой вставкой''' (англ. ''copy and paste'') $CAP(M, S, I)$ будем назвать изображение, полученное наложением части изображения $I$, заданной маской $M$, на изображение $S$. | ||
| + | $CAP(M, S, I) = I \odot M + S \odot (1 - M)$, где $\odot$ {{---}} покомпонентное умножение. }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Дискретный оператор Лапласа''' (фильтр Лапласа) $\mathbf{D}^2$ {{---}} аналог непрерывного оператора Лапласа $\nabla^2$, который позволяет выделять контуры изображения (рисунки $7.1$ и $7.2$). | ||
| + | $$\mathbf{D}^2=\begin{bmatrix}0 & 1 & 0\\1 & -4 & 1\\0 & 1 & 0\end{bmatrix}.$$ }} | ||
| + | {| class="wikitable" style="float:right; clear:right;" | ||
| + | !Рисунок $7.1$:<br>Исходное изображение<ref>https://en.wikipedia.org/wiki/Lenna#/media/File:Lenna_(test_image).png</ref> | ||
| + | !Рисунок $7.2$:<br>Применение фильтра Лапласа | ||
| + | |- | ||
| + | | [[Файл:Lenna.png|220px]] | ||
| + | | [[Файл:Lenna_Laplacian_Neg.png|220px]] | ||
| + | |} | ||
| + | |||
| + | Для сохранения контуров изображений $S$ и $I$ в области вставки воспользуемся идеей из [[Блендинг изображений#Блендинг Пуассона|метода Пуассона]] и введём следующую функцию потерь<ref name='ZWS20'/>: | ||
| + | $$\mathcal{L}_{grad}(S, I, M, O) = \displaystyle\frac{1}{2HW}\displaystyle\sum_{m=1}^H \displaystyle\sum_{n=1}^W \left[ \mathbf{D}^2 B - \left(\mathbf{D}^2 S + \mathbf{D}^2 I\right) \right]^2_{mn},$$ | ||
| + | где $H, W$ {{---}} высота и ширина изображений. $B = CAP(M, S, O)$ {{---}} блендинговое изображение, оптимизируемое относительно $O$. | ||
| + | |||
| + | Рассмотрим область $\overline{\Omega} = \{\;p \;| \;M_p = 0\; \}$. Заметим, что градиент $I$ в $\overline{\Omega}$ равен нулю. Тогда градиенты $S$ и $B$ совпадают, и задача минимизации $\mathcal{L}_{grad}$ решается только в области вставки. | ||
| + | |||
| + | На обоих этапах алгоритм минимизирует взвешенную сумму следующих функций потерь: | ||
| + | * $\mathcal{L}_{content}$ для сохранения содержания накладываемого изображения $I$. | ||
| + | * $\mathcal{L}_{style}$ для переноса стиля изображения $S$ на $I$. | ||
| + | * $\mathcal{L}_{hist}$ для стабилизации переноса стиля. | ||
| + | * $\mathcal{L}_{tv}$ для удаления шумов. | ||
| + | * $\mathcal{L}_{grad}$ для сохранения контуров фона и изображения. | ||
| + | |||
| + | <!-- 0JAg0LXRidGRINCd0LDRgdGC0Y8g0L7Rh9C10L3RjCDQvNC40LvQsNGPIQ== --> | ||
| + | Для подсчета $\mathcal{L}_{style}$ и $\mathcal{L}_{content}$ авторами статьи<ref name='ZWS20'>[https://openaccess.thecvf.com/content_WACV_2020/papers/Zhang_Deep_Image_Blending_WACV_2020_paper.pdf Deep Image Blending] Lingzhi Zhang, Tarmily Wen, Jianbo Shi (2020)</ref> использовалась сеть VGG-19<ref name="SZ14"/>, обученная на ImageNet<ref name="ImageNet">https://image-net.org/papers/imagenet_cvpr09.pdf J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. FeiFei. Imagenet: A large-scale hierarchical image database</ref>. | ||
| + | |||
| + | === Первый этап === | ||
| + | На первом этапе изображение $I$ накладывается на фоновое изображение $S$ таким образом, чтобы были незаметны швы. | ||
| + | Построение начинается с белого шума $Z$, который оптимизируется в области вставки путем минимизации суммарной функции потерь $\mathcal{L}_{total}$, представленной взвешенной суммой всех функций потерь, описанных выше: | ||
| + | $$ \mathcal{L}_{total}(Z) = w_{grad}\mathcal{L}_{grad}(I, S, B) + w_{content}\mathcal{L}_{content}(I, M, Z) + w_{style}\mathcal{L}_{style}(S, B) + w_{tv}\mathcal{L}_{tv}(B) + w_{hist}\mathcal{L}_{hist}(S, B).$$ | ||
| + | Для решения задачи минимизации авторы статьи<ref name='ZWS20' /> используют алгоритм L-BFGS<ref name="LBFGS">https://en.wikipedia.org/wiki/Limited-memory_BFGS Limited-memory BFGS - Wikipedia</ref>. | ||
| + | |||
| + | Отметим, что $\mathcal{L}_{content}$ зависит от маски и отвечает за сохранение содержания $I$ в области вставки. | ||
| + | |||
| + | Отличительной чертой этого этапа является использование функции потерь $\mathcal{L}_{grad}$, приближающей градиент результата к градиенту $I$ в области наложения, за счет чего достигается бесшовность. | ||
| + | |||
| + | В результате получается подготовительное блендинг-изображение $B$. | ||
| + | |||
| + | <font size="3em"> | ||
| + | '''fun''' $SeamlessBlending$( | ||
| + | <span style="display: inline-block; width: 3em">$I$,</span> <font color="green"> // Входное изображение </font> | ||
| + | <span style="display: inline-block; width: 3em">$M$,</span> <font color="green"> // Маска </font> | ||
| + | <span style="display: inline-block; width: 3em">$S$ </span> <font color="green"> // Стилевое изображение </font> | ||
): | ): | ||
| − | <font color="green"> | + | <font color="green">// Инициализируем первое приближение белым шумом </font> |
| − | $ | + | $Z \leftarrow RandomNoise() $ |
| − | <font color="green"> | + | $B \leftarrow CAP(M, S, Z)$ |
| − | $ | + | <font color="green">// Определим суммарную функцию потерь с весами слагаемых $w$</font> |
| − | + | $\mathcal{L}_{total}(Z) \leftarrow w_{grad}\mathcal{L}_{grad}(I, S, B) + w_{content}\mathcal{L}_{content}(I, M, Z) + w_{style}\mathcal{L}_{style}(S, B) + w_{tv}\mathcal{L}_{tv}(B) + w_{hist}\mathcal{L}_{hist}(S, B)$ | |
| + | <font color="green">// С помощью алгоритма L-BFGS ищем изображение $Z$, которое минимизирует $\mathcal{L}_{total}$ </font> | ||
| + | $Z \leftarrow Reconstruct(\mathcal{L}_{total}, Z)$ | ||
| + | '''return''' $CAP(M, S, Z)$ | ||
| + | </font> | ||
| + | |||
| + | === Второй этап === | ||
| + | |||
| + | Второй этап алгоритма представляет собой модификацию полученного на первом этапе блендинг-изображения $B$ таким образом, чтобы стиль изображения был наиболее близок к стилю $S$. | ||
| + | |||
| + | В отличие от предыдущего этапа, функция потерь не включает в себя $\mathcal{L}_{grad}$: | ||
| + | $$\mathcal{L}_{total}(O) = w_{content}\mathcal{L}_{content}(B, O) + w_{style}\mathcal{L}_{style}(S, O) + w_{tv}\mathcal{L}_{tv}(O) + w_{hist}\mathcal{L}_{hist}(S, O).$$ | ||
| + | |||
| + | Минимизация происходит относительно результата алгоритма $O$, который инициализируется изображением $B$. | ||
| − | '''fun''' | + | <font size="3em"> |
| − | + | '''fun''' $StyleRefinement$( | |
| − | + | <span style="display: inline-block; width: 3em">$B$,</span> <font color="green"> // Подготовительное блендинг-изображение, результат первого этапа </font> | |
| − | + | <span style="display: inline-block; width: 3em">$M$,</span> <font color="green"> // Маска </font> | |
| − | + | <span style="display: inline-block; width: 3em">$S$ </span> <font color="green"> // Стилевое изображение </font> | |
| − | |||
): | ): | ||
| − | $ | + | $O \leftarrow B$ |
| − | $ | + | <font color="green">// Определим суммарную функцию потерь с весами слагаемых $w$</font> |
| − | + | $\mathcal{L}_{total}(O) \leftarrow w_{cont}\mathcal{L}_{content}(B, O) + w_{style}\mathcal{L}_{style}(S, O) + w_{tv}\mathcal{L}_{tv}(O) + w_{hist}\mathcal{L}_{hist}(S, O)$ | |
| − | $O | + | <font color="green">// С помощью алгоритма L-BFGS ищем изображение $O$, которое минимизирует $\mathcal{L}_{total}$ </font> |
| − | + | $O \leftarrow Reconstruct(\mathcal{L}_{total}, O)$ | |
'''return''' $O$ | '''return''' $O$ | ||
| + | </font> | ||
| + | |||
| + | Примеры с [https://github.com/owenzlz/DeepImageBlending/tree/master/results Github авторов]: | ||
| + | |||
| + | {| | ||
| + | ! После первого этапа | ||
| + | ! После обоих этапов | ||
| + | |- | ||
| + | | [[Файл:1_first_pass.png|300px]] | ||
| + | | [[Файл:1_second_pass.png|300px]] | ||
| + | |- | ||
| + | | [[Файл:3_first_pass.png|300px]] | ||
| + | | [[Файл:3_second_pass.png|300px]] | ||
| + | |- | ||
| + | | [[Файл:5_first_pass.png|300px]] | ||
| + | | [[Файл:5_second_pass.png|300px]] | ||
| + | |} | ||
| − | == | + | ===Детали реализации=== |
| − | == | + | В статье использовались следующие значения коэффициентов: |
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Веса функций потерь | ||
| + | |- | ||
| + | ! Этап | ||
| + | ! $w_{grad}$ | ||
| + | ! $w_{content}$ | ||
| + | ! $w_{style}$ | ||
| + | ! $w_{hist}$ | ||
| + | ! $w_{tv}$ | ||
| + | |- | ||
| + | ! $1$ | ||
| + | | $10^5$ | ||
| + | | $1$ | ||
| + | | $10^5$ | ||
| + | | $1$ | ||
| + | | $10^{-6}$ | ||
| + | |- | ||
| + | ! $2$ | ||
| + | | $0$ | ||
| + | | $1$ | ||
| + | | $10^7$ | ||
| + | | $1$ | ||
| + | | $10^{-6}$ | ||
| + | |} | ||
| + | <!--Для подсчета $\mathcal{L}_{style}$ используются слои conv1_2, conv2_2, conv3_3, conv4_3 VGG-19, для $\mathcal{L}_{content}$ {{---}} conv2_2.--> | ||
| + | {| class="wikitable" | ||
| + | |+ Коэффициенты $\alpha$ и $\beta$ | ||
| + | |- | ||
| + | ! Параметр | ||
| + | ! conv1_2 | ||
| + | ! conv2_2 | ||
| + | ! conv3_3 | ||
| + | ! conv4_3 | ||
| + | |- | ||
| + | ! $\alpha$ | ||
| + | | $0$ | ||
| + | | $1$ | ||
| + | | $0$ | ||
| + | | $0$ | ||
| + | |- | ||
| + | ! $\beta$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | | $1/4$ | ||
| + | |} | ||
| + | |||
| + | На обоих этапах максимальное количество итераций алгоритма L-BFGS {{---}} $1000$. | ||
| + | |||
| + | === Примеры === | ||
| + | Примеры с [https://github.com/owenzlz/DeepImageBlending/tree/master/results Github авторов]: | ||
| + | |||
| + | [[Файл:МЛ блендинг пример.png|800px]] | ||
| + | |||
| + | ==См. также== | ||
| + | * [[Neural_Style_Transfer|Neural Style Transfer]] | ||
| + | * [[Сверточные_нейронные_сети | Свёрточная нейронная сеть]] | ||
| − | [https://en.wikipedia.org/wiki/ | + | ==Источники информации== |
| + | * [https://en.wikipedia.org/wiki/Histogram_matching Histogram matching] | ||
| + | * Patrick Perez, Michel Gangnet, Andrew Blake (2003), [https://www.cs.jhu.edu/~misha/Fall07/Papers/Perez03.pdf Poisson Image Editing]. | ||
| + | <!--* Karen Simonyan, Andrew Zisserman (2014), [https://arxiv.org/pdf/1409.1556.pdf Very Deep Convolutional Networks for Large-Scale Image Recognition]--> | ||
| + | * Leon A. Gatys, Alexander S. Ecker, Matthias Bethge (2016), [https://rn-unison.github.io/articulos/style_transfer.pdf Image Style Transfer Using Convolutional Neural Networks] | ||
| + | <!--* Eric Risser, Pierre Wilmot, Connelly Barnes (2017), [https://arxiv.org/pdf/1701.08893.pdf Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses]--> | ||
| + | <!--* Aravindh Mahendran, Andrea Vedaldi (2015), [https://arxiv.org/pdf/1412.0035.pdf Understanding Deep Image Representations by Inverting Them]--> | ||
| + | <!--* Justin Johnson, Alexandre Alahi, Li Fei-Fei (2016), [https://arxiv.org/pdf/1603.08155.pdf Perceptual Losses for Real-Time Style Transfer and Super-Resolution]--> | ||
| + | <!--* Jing Liao, Yuan Yao, Lu Yuan, Gang Hua, Sing Bing Kang (2017), [https://arxiv.org/pdf/1705.01088.pdf Visual Attribute Transfer through Deep Image Analogy]--> | ||
| + | * Fujun Luan, Sylvain Paris, Eli Shechtman, Kavita Bala (2018), [https://arxiv.org/pdf/1804.03189.pdf Deep Painterly Harmonization] | ||
| + | * Lingzhi Zhang, Tarmily Wen, Jianbo Shi (2020), [https://openaccess.thecvf.com/content_WACV_2020/papers/Zhang_Deep_Image_Blending_WACV_2020_paper.pdf Deep Image Blending] | ||
==Примечания== | ==Примечания== | ||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Нейронные сети]] | ||
| + | [[Категория: Сверточные нейронные сети]] | ||
Текущая версия на 19:44, 4 сентября 2022
Копирование элемента одного изображения и его вставка на другое изображение — один из наиболее используемых методов для создания графического контента. Простая вставка, как правило, бросается в глаза и делает результат похожим на коллаж, во многих случаях этот эффект является нежелательным.
| Определение: |
| Блендинг изображений (англ. image blending) — метод, позволяющий вставить часть одного изображения в другое таким образом, чтобы композиция изображений выглядела естественно, без швов на границах вставки. |
Основная трудность задачи заключается в том, что естественность результата зависит не только от бесшовности наложения, но и от схожести цветов и текстуры вставляемого и фонового изображений.
| Вставляемое изображение | Фоновое изображение | Простая вставка | Желаемый результат |
|---|---|---|---|

|

|

|

|
Блендинг Пуассона
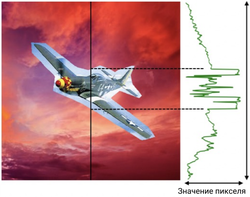
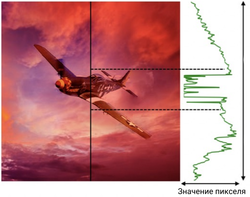
Простая вставка одного изображения поверх другого нередко влечет заметный перепад яркости на границе вставки (рисунок $1.1$). Метод Пуассона заключается в сглаживании этого перепада (рисунок $1.2$) с целью сделать дефект менее заметным, используя градиент вставляемого изображения и значения пикселей фонового изображения на границе вставки.
Замечание: Для RGB изображений задача минимизации решается для каждого цветового канала отдельно.
Давайте обозначим за $S$ изображение, которое служит фоном, а за $I$ — изображение, вставляемое поверх $S$. Область вставки будем задавать двоичной маской $M$, содержащей единицы в области наложения. Например:
| Фоновое изображение $S$ |
Накладываемое изображение $I$ |
Маска $M$ |
|---|---|---|

|

|

|
Идея подхода
Пусть замкнутое множество $P \subset \mathbb{R}^2$ — область, на которой определено изображение $S$, а замкнутое множество $\Omega \subset P$ с границей $\partial\Omega$ и внутренностью $int(\Omega)$ — область вставки изображения $I$.
Пусть $f_S$ — скалярная функция, определенная на $P \setminus int(\Omega)$, задает фоновое изображение $S$; $f$ — неизвестная скалярная функция, определенная на $int(\Omega)$, задает, каким образом должно выглядеть результат блендинга в области вставки.
$v_I$ — векторное поле, определенное на $\Omega$. В качестве $v_I$ возьмем градиент вставляемого изображения $I$: $v_I = \nabla f_I$.
Нашей задачей является поиск такой функции $f$, чтобы блендинговое изображение выглядело реалистично. Для этого минимизируем разность градиента функции $f$ и векторного поля $v_I$, считая, что $f = f_S$ на границе $\Omega$. $$ \underset{f}{\mathrm{min}} \underset{\Omega}{\iint} |\nabla f - v_I|^2, \text{где } f|_{\partial \Omega} = f_S|_{\partial \Omega}. $$ Решение задачи минимизации является единственным решением уравнения Пуассона для граничных условий Дирихле. $$\nabla^2 f = \nabla^2 f_I \text{ на } \Omega, f|_{\partial \Omega} = f_S|_{\partial \Omega}, \text{где } \nabla^2 \text{— оператор Лапласа.}$$
Дискретный случай
Пусть $p$ — координаты $(x, y)$ пикселя двухмерного изображения. За $Img_p$ обозначим значение пикселя с координатами $p$ изображения $Img$. Пусть $\Omega = \left\{ p\;|\;M_p = 1 \right\}$ — область, заданная маской $M$. Тогда $\partial \Omega$ — координаты границы вставляемой области, а $int(\Omega)$ — внутренность области.
Пусть $N_p$ — множество соседей $p$ (максимум четыре пикселя, имеющих общую границу с $p$, т.е. пиксели со следующими координатами: $(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)$). Для всех пар $(p, q)$ таких, что $q \in N_p$, введем $v_{pq} = I_p - I_q$.
Введем переменные $O_p, p \in \Omega$. Так как мы хотим сделать результат бесшовным, пиксели $O_p, p \in \partial\Omega$, сделаем равными $S_p$. Для $p, q \in int(\Omega),\; q \in N_p$ постараемся найти такое $O$, чтобы разность $O_p$ и $O_q$ была близка к $v_{pq}$. Для этого решим задачу минимизации:
$$ \underset{O_p,\; p \in \Omega}{\mathrm{min}}\; \underset{p, q \in \Omega}{\sum}\; \left(O_p - O_q - v_{pq}\right)^2, \text{где } O_p = S_p, p \in \partial \Omega. $$
Заметим, что функция, которую мы хотим минимизировать, квадратична относительно переменных $O_p, p \in int(\Omega)$. Для решения задачи минимизации вычислим частные производные по этим переменным и найдем значения переменных, при которых частные производные будут равны нулю. $$\frac{\partial{\underset{p, q \in \Omega}{\sum}\; \left(O_p - O_q - v_{pq}\right)^2}}{\partial O_p} = \underset{q \in N_p}{\sum} 2 \left(O_p - O_q - v_{pq}\right) - \underset{q \in N_p}{\sum} 2 \left(O_q - O_p - v_{qp}\right) = 2 \underset{q \in N_p}{\sum} 2 \left(O_p - O_q - v_{pq}\right).$$
Приравнивая к нулю, получаем: $|N_p| O_p - \underset{q \in N_p}{\sum} O_q = \underset{q \in N_p}{\sum} v_{pq}$.
Добавим условие $O_p = S_p, p \in \partial \Omega$: $\;|N_p| O_p - \underset{q \in N_p \cap int(\Omega)}{\sum} O_q = \underset{q \in N_p \cap \partial \Omega}{\sum} S_q + \underset{q \in N_p}{\sum} v_{pq}$.
Для решения систем уравнений такого вида могут быть использованы итеративные алгоритмы Gauss-Seidel и V-cycle multigrid[2].
Получаем значения пикселей $O_p$, $p \in int(\Omega)$. Тогда результат $B$ блендинга Пуассона будет следующим: $$ B_p = \begin{cases} O_p,\; \text{если } p \in int(\Omega) \\ S_p,\; \text{иначе } \end{cases}. $$
Mетод Пуассона сдвигает цвета накладываемого изображения, сохраняя свойства градиента (т.е. если пиксель $I_{p1}$ был меньше $I_{p2}$, то после преобразования $I_{p1}$ не станет больше $I_{p2}$), однако само значение градиета может получиться другим.[3]
Нейронный перенос стиля
Прежде чем переходить к гармонизации картин, рассмотрим задачу нейронного переноса стиля с изображения $S$ на изображение $I$. Для этого используются выходы скрытых слоёв свёрточной нейронной сети VGG-19[4] (конкретные слои указаны ниже в деталях реализации).
Основная идея генерации изображения — решение оптимизационной задачи $\mathcal{L}(I, S, O) \xrightarrow[O]{} min$, где $O$ — итоговое изображение, $\mathcal{L}(I, S, O)$ — функция потерь. Такую задачу можно решать градиентным спуском в пространстве изображений используя метод обратного распространения ошибки.
| Определение: |
| Пусть $F^l\left[I\right] \in \mathcal{R}^{N_l \times M_l}$ — матрица значений выхода $l$-го слоя сети на изображении $I$. Выход $l$-го слоя сети имеет размерность $N_l \times W_l \times H_l$. Представим его как матрицу $N_l \times M_l$, где $N_l$ — количество фильтров в $l$-ом слое, $M_l$ — количество признаков ($M_l = W_l H_l$). Тогда $F^l_{ij}\left[I\right]$ — $j$-ый признак $i$-го фильтра в $l$-ом слое. Столбец матрицы $F^l\left[I\right]$ размера $N_l$ назовём вектором активации. |
| Определение: |
| Матрица Грама (англ. Gram matrix) — матрица попарных скалярных произведений.
$$G^l\left[S\right] \in \mathcal{R}^{N_l \times N_l},$$ $$G^l\left[S\right] = F^l\left[S\right]F^l\left[S\right]^T.$$ |
Далее рассмотренны функции потерь, которые мы будем использовать.
Content loss
$F^l\left[I\right]$ отражает содержание изображения. Мы хотим чтобы содержание результата было как можно ближе к исходной картинке. Введём для этого такую функцию потерь: $$\mathcal{L}_{content}(I, O) = \displaystyle\sum_l \frac{\alpha_l}{2 N_l M_l}\displaystyle\sum_{i, j} \left(F^l_{ij}\left[I\right] - F^l_{ij}\left[O\right]\right)^2,$$ где $\alpha_l$ — вклад $l$-го слоя в функцию потерь.
Style loss
$G^l\left[S\right]$ отражает статистику выходов фильтров независимо от их расположения, что, в свою очередь, отражает стиль изображения. Чтобы стиль результата был похож на стилевое изображение, введём следующую функцию потерь: $$\mathcal{L}_{style}(S, O) = \displaystyle\sum_l \frac{\beta_l}{2N_l^2} \displaystyle\sum_{i, j} \left(G^l_{ij}\left[S\right] - G^l_{ij}\left[O\right]\right)^2,$$ где $\beta_l$ — вклад $l$-го слоя в функцию потерь.
Gatys' loss
Скомбинируем $\mathcal{L}_{content}$ и $\mathcal{L}_{style}$ и получим функцию потерь, которая была использована в алгоритме Гатиса[5]: $$\mathcal{L}_{Gatys}(I, S, O) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{style}(S, O).$$ Вес $w_{style}$, векторы $\alpha$ и $\beta$ являются, в некотором смысле, гиперпараметрами алгоритма, которые мы выберем позднее.
Histogram Loss
Авторы другой статьи[6] показывают, что результаты, полученные с помощью $\mathcal{L}_{Gatys}$ нестабильны и предложили учитывать ещё одну функцию потерь, основанную на сопоставлении гистограмм.
| Определение: |
| Сопоставление гистограмм (англ. Histogram matching) — метод обработки изображения, после которого гистограмма изображения совпадает с целевой гистограммой[7]. |
Пусть $R = histmatch(S, O)$ — отображение пикселей такое, что гистограмма $S$ совпадает с гистограммой $R(O)$, тогда Histogram loss будет выглядеть так: $$\mathcal{L}_{hist}(S, O) = \displaystyle\sum_l \gamma_l \displaystyle\sum_{i, j} \left(F^l_{ij}\left[O\right] - R\left(F^l_{ij}\left[O\right]\right)\right)^2,$$ где $\gamma_l$ — вклад $l$-го слоя в функцию потерь.
Замечание: Если в случае остальных функций потерь нетрудно посчитать производную, то здесь могут возникнуть проблемы. Но поскольку $\displaystyle\frac{\partial \mathcal{L}_{hist}}{\partial F^l_{ij}\left[O\right]}$ является нулём почти везде, авторы предлагают при подсчёте производной считать $R\left(F^l_{ij}\left[O\right]\right)$ константой, которая не зависит от $O$.
Total variation loss
Также добавим ещё одну функцию потерь, которая удаляет шумы, при этом сохраняя важные детали изображения[8][9]:
$$\mathcal{L}_{tv}(O) = \displaystyle\sum_{i, j} \left(O^l_{i, j} - O^l_{i-1, j}\right)^2 + \left(O^l_{i, j} - O^l_{i, j-1}\right)^2.$$
Глубокая гармонизация картин
Для того чтобы вставить изображение в картину или рисунок нужно не только сделать бесшовный переход и изменить цвета, но ещё и изменить текстуру вставляемого изображения, например, сымитировать мазки кистью (рисунок $2$). Используем для этого комбинацию подходов из других статей[5][9][6].
Алгоритм состоит из двух проходов. Первый проход делает грубую гармонизацию, а второй — более тщательную. Отличаются они стилевым маппингом и функциями потерь[11].
| Определение: |
| Стилевым маппингом назовём отображение $P : \mathcal{R}^{N_l \times M_l} \rightarrow \mathcal{R}^{N_l \times M_l}$, которое некоторым образом переставляет столбцы матрицы (не обязательно обратимо, то есть столбцы могут теряться и копироваться). Более формально, пусть $p(j)$ — новая позиция столбца $j$, тогда $P(Q)_{i, p(j)} = Q_{ij}$. |
Один проход состоит из $3$ частей:
- Входное $I$ и стилевое $S$ изображения подаются на вход нейронной сети VGG-19, так мы получаем $F^l_{ij}\left[I\right]$ и $F^l_{ij}\left[S\right]$.
- Для каждого слоя $l$ некоторым алгоритмом $\pi$ cтроится стилевой маппинг $P_l$, который сопоставляет столбцам из $F_l[I]$ столбцы из $F_l[S]$.
- Изображение $O$ восстанавливается градиентным спуском по пространству изображений с использованием функции потерь $\mathcal{L}$.
fun $SinglePassHarmonization$( $I$,// Входное изображение $M$,// Маска $S$,// Стилевое изображение $\pi$,// Алгоритм построения стилевого маппинга $\mathcal{L}$// Функция потерь ): // Строим матрицы $F[I]$ и $F[S]$ с помощью свёрточной сети VGG-19 $F[I] \leftarrow ComputeNeuralActivations(I)$ $F[S] \leftarrow ComputeNeuralActivations(S)$ // Строим стилевой маппинг $P \leftarrow \pi(F[I], M, F[S])$ // Градиентным спуском ищем изображение $O$, которое минимизирует $\mathcal{L}$ $O \leftarrow Reconstruct(I, M, S, P, \mathcal{L})$ return $O$
Первый проход
| Определение: |
| Патчем (англ. patch) для столбца $j$ будем называть тензор $3 \times 3 \times N_l$, который состоит из соседних векторов активации в тензоре выхода свёрточного слоя, с центром в $(x, y)$, где $j = y W_l + x$. |


Первый проход делает грубую гармонизацию, но при этом он хорошо работает с любыми стилями (рисунок $3.1$). Здесь используется алгоритм $IndependentMapping$ для построения стилевого маппинга. Этот алгоритм для каждого столбца $j$ в $F_l[I]$ ищет столбец $p(j)$ в $F_l[S]$, такой что евклидово расстояние между патчем $F_l[I]$ с центром $j$ и патчем $F_l[S]$ с центром $p(j)$ минимально (метод ближайшего соседа).
fun $IndependentMapping$( $F[I]$,// Выходы слоёв после входного изображения $Mask$,// Маска $F[S]$// Выходы слоёв после стилевого изображения ): // Для всех слоёв от $1$ до $L$ for $l \in [1 : L]$: // Для всех столбцов от $1$ до $M_l$ for $j \in [1 : M_l]$: // Рассматриваем патчи только внутри маски, которую нужно масштабировать в соответсвии с размером слоя $l$ if $j \in Resize(Mask, l)$: // Берём самый похожий стилевой патч и записываем его в маппинг. $P_l(j) \leftarrow NearestNeighborIndex(F[I], j, F[S])$ return $P$
В первом проходе используется модифицированная функция потерь $\mathcal{L}_{Gatys}$, с тем лишь отличием, что в $\mathcal{L}_{style}$ к $F_l[S]$ применяется стилевой маппинг $P_l$:
$$\mathcal{L}_1(I, S, O, P) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{style}(S, O, P).$$
Замечание: при посчёте градиента $\mathcal{L}_{content}$ используются только пиксели внутри маски[12].
Второй проход





Второй проход делает более качественную гармонизацию после первого прохода (рисунок $3.2$). Здесь мы будем использовать более сложный алгоритм $ConsistentMapping$ построения стилевого маппинга и более сложную функцию потерь. Суть этого алгоритма в том, чтобы найти стилевой мапинг на некотором слое $l_{ref}$ и перенести этот маппинг на остальные слои. Также, мы будем предпочитать маппинги, в которых смежные патчи в $F_l[S]$ остаются смежными после мапинга, чтобы обеспечить пространсвенную согласованность (таким образом мы хотим переносить сложные текстуры более качественно, например, мазки кистью). Если применять второй проход сразу, то результаты получаются хуже (рисунок $4.2$).
fun $ConsistentMapping$( $F[I]$,// Выходы слоёв после входного изображения $Mask$,// Маска $F[S]$// Выходы слоёв после стилевого изображения ): // Сначала посчитаем маппинг как в IndependentMapping только для слоя $l_{ref}$ for $j \in [1 : M_{l_{ref}}]$: if $j \in Resize(Mask, l_{ref})$: $P_0(j) \leftarrow NearestNeighborIndex(F[I], j, F[S])$ // Далее обеспечиваем пространсвенную согласованность for $j \in [1 : M_{l_{ref}}]$: if $j \in Resize(Mask, l_{ref})$: $q \leftarrow P_0(j)$ // Инициализируем множество кандидатов на новый маппинг $CSet \leftarrow \{q\}$ // Перебираем все смежные патчи for $o \in \left\{N, NE, E, SE, S, SW, W, NW\right\}$: // Добавляем в кандидаты патч, сосед которого является маппингом для нашего соседа в соответсвующем направлении $CSet \leftarrow CSet \cup \left\{P_0(j + o) - o\right\}$ // Среди всех кандидатов выбираем тот, который ближе всего к маппингам наших соседей $P_{l_{ref}}(j) \leftarrow \underset{c \in CSet}{\mathrm{argmin}}\displaystyle\sum_o \left\|(F_{l_{ref}}[S]_c - F_{l_{ref}}[S]_{P_0(j + o)}\right\|^2$ // Теперь нужно перенести маппинг для $l_{ref}$ на остальные слои for $l \in [1 : L] \setminus \{l_{ref}\}$: for $j \in [1 : M_l]$: if $j \in Resize(Mask, l)$: // Вычисляем позицию $j'$ на слое $l_{ref}$ соответствующую позиции $j$ на слое $l$ $j' \leftarrow ChangeResolution(l, l_{ref}, j)$ // Берём маппинг для позиции $j'$ $q \leftarrow P_{l_{ref}}(j')$ // Переносим позицию $q$ обратно на слой $l$ $P_l(j) \leftarrow ChangeResolution(l_{ref}, l, q)$ return $P$
При вычислении стилевого маппинга появляется очень много дублирующихся векторов, что даёт не очень хорошие результаты (рисунок $4.3$). Поэтому при вычислении матрицы Грама выкинем повторяющиеся векторы. Назовём функцию потерь с такой модификацией $\mathcal{L}_{s1}$.
$$\mathcal{L}_2(I, S, O, P) = \mathcal{L}_{content}(I, O) + w_{style}\mathcal{L}_{s1}(S, O, P) + w_{hist}\mathcal{L}_{hist}(S, O) + w_{tv}\mathcal{L}_{tv}(O),$$ где $w_{style}, w_{hist}, w_{tv}$ — веса соответсвующих функций потерь.
Итоговый алгоритм
Теперь осталось запустить две стадии:
fun $Harmonization$( $I$,// Входное изображение $Mask$,// Маска $S$// Стилевое изображение ): // Грубый проход алгоритма. Каждый слой рассматривается отдельно при построении стилевого маппинга. $I' \leftarrow SinglePassHarmonization(I, Mask, S, IndependentMapping, \mathcal{L}_1)$ // Улучшение результата. Стилевой маппинг строится консистентно для всех слоёв. $O \leftarrow SinglePassHarmonization(I', Mask, S, ConsistentMapping, \mathcal{L}_2)$ return $O$
Постобработка

Описанный алгоритм даёт хорошие результаты в целом, но при ближайшем рассмотрении могут быть артефакты (рисунок $5$). Поэтому сделаем двухступенчатую постобработку (подробное описание есть в оригинальной статье[11]):
- Переведём изображение в цветовое пространство $L*\alpha*\beta$ и применим Guided filter для a и b каналов.
- С помощью алгоритма PatchMatch[13] и того же Guided filter делаем так, чтобы все патчи выходного изображения присутсвовали в стилевом (чтобы не было новых объектов или структур).
Детали реализации

Возьмём $l_{ref}$ = conv4_1 (что будет если использовать другие слои видно на рисунке $6$). Выберем следующие веса для слоёв:
| Параметр | conv1_1 | conv2_1 | conv3_1 | conv4_1 | conv5_1 |
|---|---|---|---|---|---|
| $\alpha$ | $0$ | $0$ | $0$ | $1$ | $0$ |
| $\beta$ | $0$ | $0$ | $1/3$ | $1/3$ | $1/3$ |
| Параметр | conv1_1 | conv2_1 | conv3_1 | conv4_1 | conv5_1 |
|---|---|---|---|---|---|
| $\alpha$ | $0$ | $0$ | $0$ | $1$ | $0$ |
| $\beta$ | $1/4$ | $1/4$ | $1/4$ | $1/4$ | $0$ |
| $\gamma$ | $1/2$ | $0$ | $0$ | $1/2$ | $0$ |
Введём гиперпараметр $\tau$ и возьмём $w_{style} = w_{hist} = \tau$, $w_{tv} = \tau\frac{10}{1 + \exp(10^4 * noise(S) - 25)}$, где $noise(S) = \underset{i,j}{\mathrm{med}}\left\{\left(O^l_{i, j} - O^l_{i-1, j}\right)^2 + \left(O^l_{i, j} - O^l_{i, j-1}\right)^2\right\}$[14].
Для того чтобы подбирать $\tau$ авторы статьи использовали классификатор стилей изображений. Они взяли VGG-19, обучили её классифицировать $18$ различных стилей. Эти стили были разделены на $3$ категории с разными $\tau$. Используя $Softmax$ можно интерполировать необходимый $\tau$ по следующей таблице:
| Категория стиля | Примеры стилей | $\tau$ |
|---|---|---|
| Слабый | Барокко, Высокое Возрождение | $1$ |
| Средний | Абстрактное Искусство, Постимпрессионизм | $5$ |
| Сильный | Кубизм, Экспрессионизм | $10$ |
На рисунке $4.4$ результат алгоритма без подбора гиперпараметров. Видно, что самолёт ярче, чем остальное изображение. С подбором параметров получается более естественный результат (рисунок $4.5$).
Примеры
Примеры взяты с Github авторов.
| Исходное изображение | Простая вставка | Результат | Постобработка |
|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|
Более новые подходы
Глубокий блендинг
Алгоритм глубокого блендинга состоит из двух этапов. На первом этапе на стилевое изображения $S$ бесшовно накладывается входное изображение $I$, получается подготовительное блендинг-изображение $B$. На втором этапе $B$ модифицируется таким образом, чтобы результат по стилю был похож на $S$.
Будем считать, что на вход подаются изображения, прошедшие предварительную обработку:
- Используемая для вставки часть $I$ вырезана с помощью маски.
- $M$ и $I$ выровнены относительно $S$.
- Размеры матриц, задающих $M, S, I$, совпадают.
Примеры входных данных:
| Стилевое изображение $S$[1] |

|

|

|
|---|---|---|---|
| Накладываемое изображение $I$[1] |

|

|

|
| Определение: |
| Простой вставкой (англ. copy and paste) $CAP(M, S, I)$ будем назвать изображение, полученное наложением части изображения $I$, заданной маской $M$, на изображение $S$. $CAP(M, S, I) = I \odot M + S \odot (1 - M)$, где $\odot$ — покомпонентное умножение. |
| Определение: |
| Дискретный оператор Лапласа (фильтр Лапласа) $\mathbf{D}^2$ — аналог непрерывного оператора Лапласа $\nabla^2$, который позволяет выделять контуры изображения (рисунки $7.1$ и $7.2$). $$\mathbf{D}^2=\begin{bmatrix}0 & 1 & 0\\1 & -4 & 1\\0 & 1 & 0\end{bmatrix}.$$ |
| Рисунок $7.1$: Исходное изображение[15] |
Рисунок $7.2$: Применение фильтра Лапласа |
|---|---|

|

|
Для сохранения контуров изображений $S$ и $I$ в области вставки воспользуемся идеей из метода Пуассона и введём следующую функцию потерь[1]: $$\mathcal{L}_{grad}(S, I, M, O) = \displaystyle\frac{1}{2HW}\displaystyle\sum_{m=1}^H \displaystyle\sum_{n=1}^W \left[ \mathbf{D}^2 B - \left(\mathbf{D}^2 S + \mathbf{D}^2 I\right) \right]^2_{mn},$$ где $H, W$ — высота и ширина изображений. $B = CAP(M, S, O)$ — блендинговое изображение, оптимизируемое относительно $O$.
Рассмотрим область $\overline{\Omega} = \{\;p \;| \;M_p = 0\; \}$. Заметим, что градиент $I$ в $\overline{\Omega}$ равен нулю. Тогда градиенты $S$ и $B$ совпадают, и задача минимизации $\mathcal{L}_{grad}$ решается только в области вставки.
На обоих этапах алгоритм минимизирует взвешенную сумму следующих функций потерь:
- $\mathcal{L}_{content}$ для сохранения содержания накладываемого изображения $I$.
- $\mathcal{L}_{style}$ для переноса стиля изображения $S$ на $I$.
- $\mathcal{L}_{hist}$ для стабилизации переноса стиля.
- $\mathcal{L}_{tv}$ для удаления шумов.
- $\mathcal{L}_{grad}$ для сохранения контуров фона и изображения.
Для подсчета $\mathcal{L}_{style}$ и $\mathcal{L}_{content}$ авторами статьи[1] использовалась сеть VGG-19[4], обученная на ImageNet[16].
Первый этап
На первом этапе изображение $I$ накладывается на фоновое изображение $S$ таким образом, чтобы были незаметны швы. Построение начинается с белого шума $Z$, который оптимизируется в области вставки путем минимизации суммарной функции потерь $\mathcal{L}_{total}$, представленной взвешенной суммой всех функций потерь, описанных выше: $$ \mathcal{L}_{total}(Z) = w_{grad}\mathcal{L}_{grad}(I, S, B) + w_{content}\mathcal{L}_{content}(I, M, Z) + w_{style}\mathcal{L}_{style}(S, B) + w_{tv}\mathcal{L}_{tv}(B) + w_{hist}\mathcal{L}_{hist}(S, B).$$ Для решения задачи минимизации авторы статьи[1] используют алгоритм L-BFGS[17].
Отметим, что $\mathcal{L}_{content}$ зависит от маски и отвечает за сохранение содержания $I$ в области вставки.
Отличительной чертой этого этапа является использование функции потерь $\mathcal{L}_{grad}$, приближающей градиент результата к градиенту $I$ в области наложения, за счет чего достигается бесшовность.
В результате получается подготовительное блендинг-изображение $B$.
fun $SeamlessBlending$( $I$, // Входное изображение $M$, // Маска $S$ // Стилевое изображение ): // Инициализируем первое приближение белым шумом $Z \leftarrow RandomNoise() $ $B \leftarrow CAP(M, S, Z)$ // Определим суммарную функцию потерь с весами слагаемых $w$ $\mathcal{L}_{total}(Z) \leftarrow w_{grad}\mathcal{L}_{grad}(I, S, B) + w_{content}\mathcal{L}_{content}(I, M, Z) + w_{style}\mathcal{L}_{style}(S, B) + w_{tv}\mathcal{L}_{tv}(B) + w_{hist}\mathcal{L}_{hist}(S, B)$ // С помощью алгоритма L-BFGS ищем изображение $Z$, которое минимизирует $\mathcal{L}_{total}$ $Z \leftarrow Reconstruct(\mathcal{L}_{total}, Z)$ return $CAP(M, S, Z)$
Второй этап
Второй этап алгоритма представляет собой модификацию полученного на первом этапе блендинг-изображения $B$ таким образом, чтобы стиль изображения был наиболее близок к стилю $S$.
В отличие от предыдущего этапа, функция потерь не включает в себя $\mathcal{L}_{grad}$: $$\mathcal{L}_{total}(O) = w_{content}\mathcal{L}_{content}(B, O) + w_{style}\mathcal{L}_{style}(S, O) + w_{tv}\mathcal{L}_{tv}(O) + w_{hist}\mathcal{L}_{hist}(S, O).$$
Минимизация происходит относительно результата алгоритма $O$, который инициализируется изображением $B$.
fun $StyleRefinement$(
$B$, // Подготовительное блендинг-изображение, результат первого этапа
$M$, // Маска
$S$ // Стилевое изображение
):
$O \leftarrow B$
// Определим суммарную функцию потерь с весами слагаемых $w$
$\mathcal{L}_{total}(O) \leftarrow w_{cont}\mathcal{L}_{content}(B, O) + w_{style}\mathcal{L}_{style}(S, O) + w_{tv}\mathcal{L}_{tv}(O) + w_{hist}\mathcal{L}_{hist}(S, O)$
// С помощью алгоритма L-BFGS ищем изображение $O$, которое минимизирует $\mathcal{L}_{total}$
$O \leftarrow Reconstruct(\mathcal{L}_{total}, O)$
return $O$
Примеры с Github авторов:
| После первого этапа | После обоих этапов |
|---|---|

|

|

|

|

|

|
Детали реализации
В статье использовались следующие значения коэффициентов:
| Этап | $w_{grad}$ | $w_{content}$ | $w_{style}$ | $w_{hist}$ | $w_{tv}$ |
|---|---|---|---|---|---|
| $1$ | $10^5$ | $1$ | $10^5$ | $1$ | $10^{-6}$ |
| $2$ | $0$ | $1$ | $10^7$ | $1$ | $10^{-6}$ |
| Параметр | conv1_2 | conv2_2 | conv3_3 | conv4_3 |
|---|---|---|---|---|
| $\alpha$ | $0$ | $1$ | $0$ | $0$ |
| $\beta$ | $1/4$ | $1/4$ | $1/4$ | $1/4$ |
На обоих этапах максимальное количество итераций алгоритма L-BFGS — $1000$.
Примеры
Примеры с Github авторов:
См. также
Источники информации
- Histogram matching
- Patrick Perez, Michel Gangnet, Andrew Blake (2003), Poisson Image Editing.
- Leon A. Gatys, Alexander S. Ecker, Matthias Bethge (2016), Image Style Transfer Using Convolutional Neural Networks
- Fujun Luan, Sylvain Paris, Eli Shechtman, Kavita Bala (2018), Deep Painterly Harmonization
- Lingzhi Zhang, Tarmily Wen, Jianbo Shi (2020), Deep Image Blending
Примечания
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 Deep Image Blending Lingzhi Zhang, Tarmily Wen, Jianbo Shi (2020)
- ↑ Poisson Image Editing Patrick Perez, Michel Gangnet, Andrew Blake (2003)
- ↑ https://erkaman.github.io/posts/poisson_blending.html Poisson blending для самых маленьких
- ↑ 4,0 4,1 Very Deep Convolutional Networks for Large-Scale Image Recognition Karen Simonyan, Andrew Zisserman (2014)
- ↑ 5,0 5,1 Image Style Transfer Using Convolutional Neural Networks Leon A. Gatys, Alexander S. Ecker, Matthias Bethge (2016)
- ↑ 6,00 6,01 6,02 6,03 6,04 6,05 6,06 6,07 6,08 6,09 6,10 Stable and Controllable Neural Texture Synthesis and Style Transfer Using Histogram Losses Eric Risser, Pierre Wilmot, Connelly Barnes (2017)
- ↑ https://en.wikipedia.org/wiki/Histogram_matching
- ↑ Understanding Deep Image Representations by Inverting Them Aravindh Mahendran, Andrea Vedaldi (2015)
- ↑ 9,0 9,1 Perceptual Losses for Real-Time Style Transfer and Super-Resolution Justin Johnson, Alexandre Alahi, Li Fei-Fei (2016)
- ↑ Visual Attribute Transfer through Deep Image Analogy Jing Liao, Yuan Yao, Lu Yuan, Gang Hua, Sing Bing Kang (2017)
- ↑ 11,0 11,1 11,2 https://arxiv.org/pdf/1804.03189.pdf Fujun Luan, Sylvain Paris, Eli Shechtman, Kavita Bala (2018)
- ↑ https://github.com/luanfujun/deep-painterly-harmonization/blob/a33a9a70366b6baff1cc0291f857b5895b271fc1/neural_gram.lua#L349
- ↑ https://www.researchgate.net/profile/Eli_Shechtman/publication/220184392_PatchMatch_A_Randomized_Correspondence_Algorithm_for_Structural_Image_Editing/links/02e7e520897b12bf0f000000.pdf Connelly Barnes, Eli Shechtman, Adam Finkelstein, Dan B Goldman (2009)
- ↑ [https://github.com/luanfujun/deep-painterly-harmonization/blob/a33a9a70366b6baff1cc0291f857b5895b271fc1/neural_paint.lua#L470 код функции $noise$.
- ↑ https://en.wikipedia.org/wiki/Lenna#/media/File:Lenna_(test_image).png
- ↑ https://image-net.org/papers/imagenet_cvpr09.pdf J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. FeiFei. Imagenet: A large-scale hierarchical image database
- ↑ https://en.wikipedia.org/wiki/Limited-memory_BFGS Limited-memory BFGS - Wikipedia

