Участник:Fad Oleg — различия между версиями
Fad Oleg (обсуждение | вклад) (→Полнота стандартного базиса) |
Fad Oleg (обсуждение | вклад) |
||
| (не показана 21 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | == Представление булевых функций == | ||
| + | |||
| + | Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций <tex>\Sigma = \{f_1,\ldots,f_n\}</tex>. Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре <tex>\Sigma</tex>, который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы: | ||
| + | * Как построить по данной функции представляющую её формулу? | ||
| + | * Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию? | ||
| + | ** В частности: существует ли способ приведения произвольной формулы к эквивалентной её ''канонической'' форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают? | ||
| + | * Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это? | ||
| + | |||
| + | Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций. | ||
| + | |||
| + | === Дизъюнктивная нормальная форма (ДНФ) === | ||
| + | |||
| + | {{main|ДНФ}} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Дизъюнктивная нормальная форма (ДНФ)''' (англ. ''disjunctive normal form, DNF'') {{---}} нормальная форма, в которой [[Определение булевой функции|булева функция]] задана как дизъюнкция некоторого числа простых конъюнктов. | ||
| + | }} | ||
| + | Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ. | ||
| + | |||
| + | '''Примеры ДНФ:''' | ||
| + | |||
| + | <tex>f(x,y,z) = (x \land y) \lor (y \land \neg {z})</tex>. | ||
| + | |||
| + | <tex>f(x,y,z,t,m) = (x \land z) \lor (y \land x \land \neg{t}) \lor (x \land \neg {m}) </tex>. | ||
| + | |||
| + | === Конъюнктивная нормальная форма (КНФ) === | ||
| + | |||
| + | {{main|КНФ}} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Конъюнктивная нормальная форма, КНФ''' (англ. ''conjunctive normal form, CNF'') {{---}} нормальная форма, в которой [[Определение булевой функции|булева функция]] имеет вид конъюнкции нескольких простых дизъюнктов. | ||
| + | }} | ||
| + | Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ. | ||
| + | |||
| + | '''Пример КНФ:''' | ||
| + | |||
| + | <tex>f(x,y,z) = (x \lor y) \land (y \lor \neg{z})</tex> | ||
| + | |||
| + | <tex>f(x,y,z,t) = (x \lor t) \land (y \lor \neg{t}) \land (\neg{t} \lor \neg{z}) \land (\neg{x} \lor \neg{y} \lor z)</tex> | ||
| + | |||
| + | <tex>f(x,y,z,t,m) = (x \lor m \lor \neg{y}) \land (y \lor \neg{t}) \land (y \lor t \lor \neg{x})</tex> | ||
| + | |||
| + | === Полином Жегалкина === | ||
| + | |||
| + | {{main|Полином Жегалкина}} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Полином Жегалкина''' (англ. ''Zhegalkin polynomial'') {{---}} полином с коэффициентами вида <tex>0</tex> и <tex>1</tex>, где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. | ||
| + | }} | ||
| + | Полином Жегалкина имеет следующий вид: | ||
| + | |||
| + | <tex>P = a_{000\ldots000} \oplus a_{100\ldots0} x_1 \oplus a_{010\ldots0} x_2 \oplus \ldots \oplus a_{00\ldots01} x_n \oplus a_{110\ldots0} x_1 x_2 \oplus \ldots \oplus a_{00\ldots011} x_{n-1} x_n \oplus \ldots \oplus a_{11\ldots1} x_1 x_2 \ldots x_n </tex> | ||
| + | |||
| + | С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: <tex>\bigl\langle \wedge, \oplus, 1 \bigr\rangle</tex>, который, в свою очередь, по [[Теорема Поста о полной системе функций|теореме Поста]] является полным. | ||
| + | |||
| + | '''Примеры:''' | ||
| + | |||
| + | <tex>f(x_1,x_2) = 1 \oplus x_1 \oplus x_1 x_2 </tex> | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3) = x_1 \oplus x_1 x_2 \oplus x_2 x_3 </tex> | ||
| + | |||
| + | <tex>f(x_1,x_2,x_3,x_4) = 1 \oplus x_1 \oplus x_4 \oplus x_1 x_2 \oplus x_1 x_4 \oplus x_2 x_4 \oplus x_1 x_2 x_4 </tex> | ||
| + | |||
| + | ===Тождественные функции. Выражение функций друг через друга=== | ||
| + | |||
| + | {{Определение | ||
| + | |definition = '''Тождественные функции''' — функции, которые при любых одинаковых аргументах принимают равные значения. | ||
| + | }} | ||
| + | Приведение тождественной функции есть '''выражение булевой функции через другие'''. | ||
| + | |||
| + | Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие. | ||
| + | {{Пример | ||
| + | |example=Выразим следующие функции через систему функций <tex>\{\land, \lor, \lnot \} </tex>. | ||
| + | |||
| + | <tex> x \oplus y = \left ( x \land \lnot y \right ) \lor \left ( \lnot x \land y \right ) = \left ( x \lor \lnot y \right ) \land \left ( \lnot x \lor y \right )</tex> | ||
| + | |||
| + | <tex> x \downarrow y = \lnot \left ( x \lor y \right) = \lnot x \land \lnot y</tex> | ||
| + | |||
| + | <tex>\langle x, y, z \rangle = \left ( x \land y \right ) \lor \left ( y \land z \right ) \lor \left ( x \land z \right ) = \left ( x \lor y \right ) \land \left ( y \lor z \right ) \land \left ( x \lor z \right )</tex> | ||
| + | }} | ||
| + | === Подстановка одной функции в другую === | ||
| + | |||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Подстановкой''' (англ. ''substitution'') функции <tex>g</tex> в функцию <tex>f</tex> называется замена <tex>i</tex>-того аргумента функции <tex>f</tex> значением функции <tex>g</tex>: | ||
| + | |||
| + | <center><tex>h(x_{1}, \ldots, x_{n+m-1}) = f(x_{1}, \ldots, x_{i-1}, g(x_{i}, \ldots, x_{i+m-1}), x_{i+m}, \ldots, x_{n+m-1})</tex></center> | ||
| + | }} | ||
| + | Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя. | ||
| + | |||
| + | При подстановке функции <tex>g</tex> вместо <tex>i</tex>-того аргумента функции <tex>f</tex>, результирующая функция <tex>h</tex> будет принимать аргументы, которые можно разделить на следующие блоки: | ||
| + | |||
| + | {| | ||
| + | |1. <tex> x_{1}, \ldots, x_{i-1}</tex> | ||
| + | |{{---}} аргументы функции <tex>f</tex> до подставленного значения функции <tex>g</tex> | ||
| + | |- | ||
| + | |2. <tex> x_{i}, \ldots, x_{i+m-1} </tex> | ||
| + | |{{---}} используются как аргументы для вычисления значения функции <tex>g(y_{1}, \ldots, y_{m})</tex> | ||
| + | |- | ||
| + | |3. <tex> x_{i+m}, \ldots, x_{n+m-1} </tex> | ||
| + | |{{---}} аргументы функции <tex>f</tex> после подставленного значения функции <tex>g</tex> | ||
| + | |} | ||
| + | {{Пример | ||
| + | |example=Исходные функции: | ||
| + | #<tex> f(a,b) = a \vee b </tex> | ||
| + | #<tex> g(a) = \neg a </tex> | ||
| + | |||
| + | <tex> h(a,b) = f(a,g(b)) = a \vee \neg b </tex> {{---}} подстановка функции <tex>g</tex> вместо второго аргумента функции <tex>f</tex>. В данном примере при помощи подстановки мы получили функцию <tex>h(a,b)=a \leftarrow b</tex>. | ||
| + | }} | ||
| + | === Отождествление переменных === | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Отождествлением переменных''' (англ. ''identification of variables'') называется подстановка <tex>i</tex>-того аргумента функции <tex>f</tex> вместо <tex>j</tex>-того аргумента: | ||
| + | |||
| + | <center><tex>h(x_{1}, \ldots, x_{j-1}, x_{j+1}, \ldots, x_{n}) = f(x_{1}, \ldots, x_{i}, \ldots, x_{j-1}, x_{i}, x_{j+1}, \ldots, x_{n})</tex></center> | ||
| + | }} | ||
| + | Таким образом, при отождествлении <tex>c</tex> переменных мы получаем функцию <tex>h</tex> с количеством аргументов <tex>n-c+1</tex>. | ||
| + | {{Пример | ||
| + | |example=<tex> f(a,b) = a \vee b </tex> {{---}} исходная функция | ||
| + | |||
| + | <tex> h(a) = a \vee a </tex> {{---}} функция с отождествленными первым и вторым аргументами | ||
| + | |||
| + | Очевидно, в данном примере мы получили функцию <tex>P_{1}</tex> {{---}} проектор единственного аргумента. | ||
| + | }} | ||
| + | === Схемы из функциональных элементов === | ||
| + | {{main|Реализация булевой функции схемой из функциональных элементов}} | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Схема из функциональных элементов, логическая схема''' (англ. ''logic diagram'') {{---}} размеченный ориентированный граф без циклов, в некотором базисе <tex>B</tex>, в котором: | ||
| + | |||
| + | 1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); | ||
| + | |||
| + | 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса <tex>B</tex>). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса <tex>B</tex>. | ||
| + | }} | ||
| + | Отождествление переменных осуществляется при помощи ветвления проводников. | ||
| + | |||
| + | Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию. | ||
| + | |||
| + | '''Некоторые логические элементы:''' | ||
| + | |||
| + | {| class = "wikitable" border = "1" | ||
| + | !-align="center" |И | ||
| + | !-align="center" |ИЛИ | ||
| + | !-align="center" |НЕ | ||
| + | !Штрих Шеффера | ||
| + | !Стрелка Пирса | ||
| + | |- | ||
| + | |[[Image:AND_logic_element.png]] | ||
| + | |[[Image:OR_logic_element.png]] | ||
| + | |[[Image:NOT_logic_element.png]] | ||
| + | |[[Image:NAND_logic_element.png]] | ||
| + | |[[Image:NOR_logic_element.png]] | ||
| + | |} | ||
| + | |||
==Стандартный базис== | ==Стандартный базис== | ||
| Строка 7: | Строка 161: | ||
}} | }} | ||
| − | + | Если рассматривать множество бинарных булевых функций <tex>P_2(2)</tex>, то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы <tex> 0 </tex> с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания: | |
<tex> x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) </tex> | <tex> x \leftrightarrow y = \left ( x \rightarrow y \right ) \land \left ( y \rightarrow x \right ) </tex> | ||
| Строка 14: | Строка 168: | ||
<tex> 0 = x \land \lnot x </tex> | <tex> 0 = x \land \lnot x </tex> | ||
| + | |||
| + | Функции <tex> \mid \ и \downarrow</tex> являются отрицаниями функций <tex> \land \ и \ \lor</tex> соответственно. | ||
| + | |||
| + | <tex> x \mid y = \lnot \left ( x \land y \right )</tex> | ||
| + | |||
| + | <tex> x \downarrow y = \lnot \left ( x \lor y \right )</tex> | ||
| + | |||
| + | Тождественность функций можно доказать с помощью таблицы истинности. | ||
| + | |||
| + | '''Пример:''' | ||
| + | |||
| + | Выразим через стандартный базис обратную импликацию <tex> \left (x \leftarrow y \right ) </tex>. | ||
| + | |||
| + | <tex>x \leftarrow y = \lnot x \rightarrow \lnot y = x \lor \lnot y </tex> | ||
==Полнота стандартного базиса== | ==Полнота стандартного базиса== | ||
| Строка 19: | Строка 187: | ||
{{Утверждение | {{Утверждение | ||
|statement = Стандартный базис является [[Полные системы функций. Теорема Поста о полной системе функций|полной системой булевых функций]] | |statement = Стандартный базис является [[Полные системы функций. Теорема Поста о полной системе функций|полной системой булевых функций]] | ||
| − | |proof = Данное утверждение - следствие [[СДНФ|теоремы об СДНФ]]. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. | + | |proof = Данное утверждение - следствие [[СДНФ|теоремы об СДНФ]]. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше. |
}} | }} | ||
| − | '''Замечание:''' | + | '''Замечание:''' |
| + | |||
| + | По [[Множества|закону де Моргана]]: | ||
<tex> x \land y = \lnot \left (\lnot x \lor \lnot y \right ) </tex> | <tex> x \land y = \lnot \left (\lnot x \lor \lnot y \right ) </tex> | ||
| Строка 34: | Строка 204: | ||
<tex> \{ \lor , \lnot \} </tex> (дизъюнктивный базис Буля) | <tex> \{ \lor , \lnot \} </tex> (дизъюнктивный базис Буля) | ||
| − | == | + | ==Теоремы о числе функций в базисе== |
| + | {{Теорема | ||
| + | |statement = Максимально возможное число булевых функций в безызбыточном базисе — четыре. | ||
| + | |proof = Рассмотрим произвольный безызбыточный базис <tex> X</tex>. Тогда по [[Полные системы функций. Теорема Поста о полной системе функций|теореме Поста]] <tex>X</tex> содержит следующие функции (не обязательно различные): | ||
| + | |||
| + | <tex>f_0 \notin T_0, f_1 \notin T_1, f_s \notin S, f_m \notin M, f_l \notin L</tex>, где <tex> T_0, T_1, S, M, L</tex> — классы Поста. | ||
| + | |||
| + | Значит, так как <tex>X</tex> — безызбыточный базис, а система <tex>\{f_0, f_1, f_s, f_m, f_l \}</tex> — полная, то <tex>\left | X \right | \le 5</tex> | ||
| + | |||
| + | Рассмотрим <tex>f_0</tex>. Возможны два случая: | ||
| + | |||
| + | 1. <tex> f_0(1, 1, \ldots, 1) = 0 </tex>, тогда <tex>f_0</tex> также не сохраняет единицу и немонотонная, т.е. | ||
| + | |||
| + | <tex> f_0 = f_1 = f_m </tex>. Значит, <tex>\left | X \right | \le 3</tex>. | ||
| + | |||
| + | 2. <tex> f_0(1, 1, \ldots, 1) = 1 </tex>, тогда <tex>f_0</tex> несамодвойственная, т.е. | ||
| + | |||
| + | <tex> f_0 = f_s </tex>. Значит, <tex>\left | X \right | \le 4</tex>. | ||
| + | }} | ||
| + | |||
{{Теорема | {{Теорема | ||
| − | |statement = | + | |statement= Для любого числа <tex>k, 1 \le k \le 4 </tex> найдётся базис <tex> X</tex>, что <tex>\left | X \right | = k</tex>. |
| − | |proof = | + | |proof=Приведём примеры базисов для каждого <tex>k</tex>: |
| − | <tex> | + | |
| + | <tex>k = 1 \Rightarrow X = \{ \downarrow \}</tex>; | ||
| + | |||
| + | <tex>k = 2 \Rightarrow X = \{ \lnot, \land \}</tex>; | ||
| + | |||
| + | <tex>k = 3 \Rightarrow X = \{ \land, \oplus, 1\}</tex>; | ||
| + | |||
| + | <tex>k = 4 \Rightarrow X = \{ 0, 1, x\land y, x\oplus y\oplus z\}</tex>; | ||
| + | |||
| + | Докажем, что последняя система является базисом: | ||
| + | |||
| + | <tex> 0 \notin T_1</tex>; | ||
| + | |||
| + | <tex> 1 \notin T_0</tex>; | ||
| − | + | <tex> x\land y \notin L\ и\ S</tex>; | |
| − | + | <tex> x\oplus y\oplus z \notin M</tex> | |
| − | + | (доказывается с помощью таблицы истинности). | |
}} | }} | ||
Текущая версия на 16:22, 27 июня 2021
Содержание
Представление булевых функций
Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре , который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:
- Как построить по данной функции представляющую её формулу?
- Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
- В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
- Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
Дизъюнктивная нормальная форма (ДНФ)
| Определение: |
| Дизъюнктивная нормальная форма (ДНФ) (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция задана как дизъюнкция некоторого числа простых конъюнктов. |
Любая булева формула благодаря использованию закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в ДНФ.
Примеры ДНФ:
.
.
Конъюнктивная нормальная форма (КНФ)
| Определение: |
| Конъюнктивная нормальная форма, КНФ (англ. conjunctive normal form, CNF) — нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов. |
Любая булева формула с помощью использования закона двойного отрицания, закона де Моргана и закона дистрибутивности может быть записана в КНФ.
Пример КНФ:
Полином Жегалкина
| Определение: |
| Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. |
Полином Жегалкина имеет следующий вид:
С помощью полинома Жегалкина можно выразить любую булеву функцию, так как он строится из следующего набора функций: , который, в свою очередь, по теореме Поста является полным.
Примеры:
Тождественные функции. Выражение функций друг через друга
| Определение: |
| Тождественные функции — функции, которые при любых одинаковых аргументах принимают равные значения. |
Приведение тождественной функции есть выражение булевой функции через другие.
Запись булевой функции в ДНФ, КНФ, а также выражение с помощью полинома Жегалкина — способы выражения одних булевых функций через другие.
| Пример: |
| Выразим следующие функции через систему функций .
|
Подстановка одной функции в другую
| Определение: |
| Подстановкой (англ. substitution) функции в функцию называется замена -того аргумента функции значением функции :
|
Допускается также не только подстановка одной функции в другую, но и подстановка функции в саму себя.
При подстановке функции вместо -того аргумента функции , результирующая функция будет принимать аргументы, которые можно разделить на следующие блоки:
| 1. | — аргументы функции до подставленного значения функции |
| 2. | — используются как аргументы для вычисления значения функции |
| 3. | — аргументы функции после подставленного значения функции |
| Пример: |
| Исходные функции:
|
Отождествление переменных
| Определение: |
| Отождествлением переменных (англ. identification of variables) называется подстановка -того аргумента функции вместо -того аргумента:
|
Таким образом, при отождествлении переменных мы получаем функцию с количеством аргументов .
| Пример: |
| — исходная функция
— функция с отождествленными первым и вторым аргументами Очевидно, в данном примере мы получили функцию — проектор единственного аргумента. |
Схемы из функциональных элементов
| Определение: |
| Схема из функциональных элементов, логическая схема (англ. logic diagram) — размеченный ориентированный граф без циклов, в некотором базисе , в котором:
1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные); 2. в каждую из остальных вершин входит одно или более ребер (зависит от выбранного базиса ). Такие вершины называются функциональными элементами и реализуют какую-либо булеву функцию из базиса . |
Отождествление переменных осуществляется при помощи ветвления проводников.
Чтобы осуществить подстановку одной функции в другую нужно выход логического элемента, который реализует первую функцию, направить на вход логического элемента, который реализует вторую функцию.
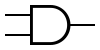
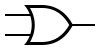
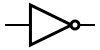
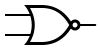
Некоторые логические элементы:
| И | ИЛИ | НЕ | Штрих Шеффера | Стрелка Пирса |
|---|---|---|---|---|
|
|
|

|
|
Стандартный базис
| Определение: |
| Стандартный базис — система булевых функций: |
Если рассматривать множество бинарных булевых функций , то для выражения любой булевой функции данного множества (кроме стрелки Пирса и штриха Шеффера) через стандартный базис достаточно выразить тождественные функции для эквиваленции, импликации и константы с использованием функций, принадлежащих стандартному базису, т. к. все остальные операции можно выразить через данные 3 функции с помощью отрицания:
Функции являются отрицаниями функций соответственно.
Тождественность функций можно доказать с помощью таблицы истинности.
Пример:
Выразим через стандартный базис обратную импликацию .
Полнота стандартного базиса
| Утверждение: |
Стандартный базис является полной системой булевых функций |
| Данное утверждение - следствие теоремы об СДНФ. Если рассмотреть функцию, не равную тождественному нулю, то она представима в виде СДНФ, в которой используются функции стандартного базиса. Способ выражения тождественного нуля через функции стандартного базиса уже был описан выше. |
Замечание:
Следовательно, стандартный базис является избыточным, в то время как безызбыточными являются подмножества системы:
(конъюнктивный базис Буля)
(дизъюнктивный базис Буля)
Теоремы о числе функций в базисе
| Теорема: |
Максимально возможное число булевых функций в безызбыточном базисе — четыре. |
| Доказательство: |
|
Рассмотрим произвольный безызбыточный базис . Тогда по теореме Поста содержит следующие функции (не обязательно различные): , где — классы Поста. Значит, так как — безызбыточный базис, а система — полная, то Рассмотрим . Возможны два случая: 1. , тогда также не сохраняет единицу и немонотонная, т.е. . Значит, . 2. , тогда несамодвойственная, т.е. . Значит, . |
| Теорема: |
Для любого числа найдётся базис , что . |
| Доказательство: |
|
Приведём примеры базисов для каждого : ; ; ; ; Докажем, что последняя система является базисом: ; ; ; (доказывается с помощью таблицы истинности). |
Источники
Полные системы булевых функций — Википедия
Категория: Дискретная математика и алгоритмы
Категория: Булевы функции