Оценка качества в задачах классификации — различия между версиями
Melmon (обсуждение | вклад) м (→Различные виды агрегации Precision и Recall: Добавила графики линий уровня) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 4 участников) | |||
| Строка 5: | Строка 5: | ||
* '''FN''' — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу. | * '''FN''' — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу. | ||
| − | Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное | + | Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное число объектов класса 0 (для бинарного случая 0/1) может выражаться как <math>\text{TP₀ + FN₀ = FP₁ + TN₁}</math> |
'''Confusion matrix''' ('''матрица ошибок / несоответствий / потерь, CM''') | '''Confusion matrix''' ('''матрица ошибок / несоответствий / потерь, CM''') | ||
| − | — квадратная матрица размера k × k, где <tex> | + | [[Файл:F_scores_сomputing.png|thumb|right|150px|Вычисление TP, FP, FN по CM]] |
| + | — квадратная матрица размера k × k, где <tex>\text{CM}_{t,c}</tex> — число объектов класса <math>t</math>, | ||
которые были квалифицированны как класс <math>c</math>, а <math>k</math> — число классов. Значения ячеек CM могут быть вычислены по формуле: | которые были квалифицированны как класс <math>c</math>, а <math>k</math> — число классов. Значения ячеек CM могут быть вычислены по формуле: | ||
| − | <tex>CM(y, \hat{y})_{t,c} = | + | <tex>\text{CM}(y, \hat{y})_{t,c} = |
| − | \displaystyle\sum_{i = 1}^{n}[(y_i = t) ∧ (\hat{y_i} = c)]</tex>, где <tex>y_i</tex> | + | \displaystyle\sum_{i = 1}^{n}[(y_i = t) ∧ (\hat{y_i} = c)]</tex>, где <tex>y_i</tex> — реальный класс объекта, а <tex>\hat{y_i}</tex> — предсказанный. |
Для бинарного случая: | Для бинарного случая: | ||
| Строка 53: | Строка 54: | ||
|} | |} | ||
В этом случае TP, TN, FP и FN считаются относительно некоторого класса <math>(i)</math> следующим образом: | В этом случае TP, TN, FP и FN считаются относительно некоторого класса <math>(i)</math> следующим образом: | ||
| − | : <tex> | + | : <tex>\text{TP}_i = T_i</tex> |
| − | : <tex> | + | : <tex>\text{FP}_i = \sum\limits_{c \in \text{Classes}} \text{F}_{i,c}</tex> |
| − | : <tex> | + | : <tex>\text{FN}_i = \sum\limits_{c \in \text{Classes}} \text{F}_{c,i}</tex> |
| − | : <tex> | + | : <tex>\text{TN}_i = \text{All - TP}_i - \text{FP}_i - \text{FN}_i</tex> |
= Простые оценки = | = Простые оценки = | ||
* '''Accuracy''' — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов. | * '''Accuracy''' — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов. | ||
| − | : <tex>Acc = \dfrac{TP + TN}{TP + TN + FP + FN}</tex> | + | : <tex>\text{Acc} = \dfrac{\text{TP + TN}}{\text{TP + TN + FP + FN}}</tex> |
* '''Recall''' — (полнота, '''sensitivity''', '''TPR''' (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса. | * '''Recall''' — (полнота, '''sensitivity''', '''TPR''' (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса. | ||
| − | : <tex>Recall = \dfrac{TP}{TP + FN}</tex> | + | : <tex>\text{Recall} = \dfrac{\text{TP}}{\text{TP + FN}}</tex> |
* '''Precision''' — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор. | * '''Precision''' — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор. | ||
| − | : <tex> | + | : <tex>\text{Precision} = \dfrac{\text{TP}}{\text{TP + FP}}</tex> |
* '''Specificity''' — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно '''не''' относит объекты к классу. | * '''Specificity''' — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно '''не''' относит объекты к классу. | ||
| − | : <tex> | + | : <tex>\text{Specificity} = \dfrac{\text{TN}}{\text{FP + TN}}</tex> |
* '''Fall-out''' — ('''FPR''' (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу. | * '''Fall-out''' — ('''FPR''' (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу. | ||
| − | : <tex>FPR = \dfrac{FP}{FP + TN}</tex> | + | : <tex>\text{FPR} = \dfrac{\text{FP}}{\text{FP + TN}}</tex> |
Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации): | Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации): | ||
* '''Precision''' | * '''Precision''' | ||
| − | : <tex> | + | : <tex>\text{Precision}_W = \dfrac{\sum\limits_{i = 1}^{k} \dfrac{T_i P_i}{C_i}}{\text{All}}</tex> |
* '''Recall''' | * '''Recall''' | ||
| − | : <tex> | + | : <tex>\text{Recall}_W = \dfrac{\sum\limits_{i = 1}^{k} T_i}{\text{All}}</tex> |
= Различные виды агрегации Precision и Recall = | = Различные виды агрегации Precision и Recall = | ||
| + | |||
| + | ''Примеры и картинки взяты из лекций курса «Введение в машинное обучение»<ref>https://web.archive.org/web/20220226120201/https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie</ref> К.В. Воронцова'' | ||
'''Арифметическое среднее:''' | '''Арифметическое среднее:''' | ||
[[Файл:EX1.png|thumb|145px|Линии уровня для среднего арифметического]] | [[Файл:EX1.png|thumb|145px|Линии уровня для среднего арифметического]] | ||
| − | : < | + | : <math>A = \dfrac{1}{2} (\text{precision + recall})</math> |
* Если precision = 0.05, recall = 1, то A = 0.525 | * Если precision = 0.05, recall = 1, то A = 0.525 | ||
| Строка 92: | Строка 95: | ||
[[Файл:EX2.png|thumb|145px|Линии уровня для минимума]] | [[Файл:EX2.png|thumb|145px|Линии уровня для минимума]] | ||
| − | : <tex>M = min(precision, recall)</tex> | + | : <tex>\text{M = min(precision, recall)}</tex> |
* Если precision = 0.05, recall = 1, то M = 0.05 | * Если precision = 0.05, recall = 1, то M = 0.05 | ||
| Строка 104: | Строка 107: | ||
[[Файл:EX3.png|thumb|145px|Линии уровня для F-меры]] | [[Файл:EX3.png|thumb|145px|Линии уровня для F-меры]] | ||
| − | : <tex>F = \dfrac{2 | + | : <tex>\text{F} = \dfrac{2 \cdot \text{precision} \cdot \text{recall}}{\text{precision + recall}}</tex> |
* Если precision = 0.05, recall = 1, то F = 0.1. | * Если precision = 0.05, recall = 1, то F = 0.1. | ||
| Строка 112: | Строка 115: | ||
Является наиболее точным усреднением, учитывает оба показателя. | Является наиболее точным усреднением, учитывает оба показателя. | ||
| − | = | + | '''Геометрическое среднее, или Индекс Фоулкса–Мэллова (Fowlkes–Mallows index)''' |
| − | + | : <math> \text{FM} = \sqrt{ \dfrac{\text{TP}}{\text{TP + FP}} \cdot \dfrac{\text{TP}}{\text{TP + FN}} }</math> | |
| + | Менее строгая мера. | ||
| − | Для наглядной оценки качества алгоритма применяется [https://ru.wikipedia.org/wiki/ROC-кривая ROC кривая]. Кривая строится на плоскости, определённой '''TPR''' (по оси ординат) и '''FPR''' (по оси абсцисс). | + | = F-мера = |
| + | |||
| + | Для общей оценки качества классификатора часто используют F₁-меру. Оригинально она вычисляется для позитивного класса случая бинарной классификации, обобщается с помощью приниципа «один против всех» (описан подробнее ниже, для многоклассовой классификации). F₁-мера — среднее гармоническое между precision и recall: | ||
| + | : <tex>\text{F}_1 = \left ( \dfrac{\text{precision}^{-1} + \text{recall}^{-1}}{2} \right )^{-1} = 2 \cdot \dfrac{\text{precision} \cdot \text{recall}}{\text{precision + recall}}</tex> | ||
| + | |||
| + | Среднее гармоническое '''взвешенное''' F<sub>β</sub> (F<sub>1</sub>-мера — частный случай F<sub>β</sub>-меры для β = 1). | ||
| + | F<sub>β</sub> измеряет эффективность классификатора учитывая recall в β раз более важным чем precision: | ||
| + | : <tex>\text{F}_β = (1 + β^2) \dfrac{\text{Precision} \cdot \text{Recall}}{β^2 \cdot \text{Precision + Recall}}</tex> | ||
| + | |||
| + | '''F-мера для многоклассовой классификации. Три вида усреднения''' | ||
| + | [[Файл:F_scores.png|thumb|400px|Принцип усреднения различных F-мер для нескольких классов]] | ||
| + | [[Файл:F_scores_сomputing.png|thumb|left|150px|Вычисление TP, FP, FN для многоклассовой классификации]] | ||
| + | |||
| + | Для вычисления F-меры (и других) метрик в рамках многоклассовой классификации используется подход «один против всех»: каждый класс ровно один раз становится «положительным», | ||
| + | а остальные — отрицательным (пример вычисления изображён на матрице). | ||
| + | |||
| + | Таким образом, в зависимости от этапа вычисления, на котором производится усреднение, можно вычислить micro-average, macro-average и average F-меры (логика вычисления изображена на схеме справа). | ||
| + | Микро- и макро-: | ||
| + | : <tex>\text{F} = 2 \cdot \dfrac{\text{precision} \cdot \text{recall}}{\text{precision + recall}}</tex>, | ||
| + | |||
| + | где для micro-average precision и recall вычислены из усреднённых TP, FP, FN; | ||
| + | |||
| + | для macro-average precision и recall вычислены из усреднённых precision<sub>i</sub>, recall<sub>i</sub>; | ||
| + | |||
| + | Усреднённая: | ||
| + | : <math>\text{F} = \dfrac{1}{k} \displaystyle\sum_{i = 0}^{k} {\text{F}_1score_i}</math>, | ||
| + | где <math>i</math> — индекс класса, а <math>k</math> — число классов. | ||
| + | |||
| + | = ROC-кривая = | ||
| + | [[Файл:ROC.png|thumb|300px|ROC-кривая; оранжевым показан идеальный алгоритм, фиолетовым — типичный, а синим — худший]] | ||
| + | |||
| + | Для наглядной оценки качества алгоритма применяется [https://ru.wikipedia.org/wiki/ROC-кривая ROC-кривая]. Кривая строится на плоскости, определённой '''TPR''' (по оси ординат) и '''FPR''' (по оси абсцисс). | ||
| + | |||
| + | Для построении графика используется мягкая классификация: вместо того, чтобы чётко отнести объект к классу, классификатор возвращает вероятности принадлежности объекта к различным классам. Эта уверенность сравнивается с порогом (какой уверенности «достаточно», чтобы отнести объект к положительному классу). В зависимости от значения этого порога меняются значения TPR и FPR. | ||
Алгоритм построения кривой: | Алгоритм построения кривой: | ||
| Строка 133: | Строка 170: | ||
Для численной оценки алгоритма по ROC-кривой используется значение площади под ней ('''AUC''', area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5. | Для численной оценки алгоритма по ROC-кривой используется значение площади под ней ('''AUC''', area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5. | ||
| + | |||
| + | С другой стороны, для построения ROC-кривой не обязательно пересчитывать TPR и FPR. | ||
| + | |||
| + | Существует '''альтернативный алгоритм построения ROC-кривой'''. | ||
| + | |||
| + | # сортируем объекты по уверенности классификатора в их принадлежности к положительному классу | ||
| + | # начинаем в точке (0, 0) | ||
| + | # последовательно продолжаем кривую вверх: | ||
| + | #* для каждого «отрицательного» объекта вверх | ||
| + | #* для каждого «положительного» — вправо. | ||
| + | |||
| + | Корректность алгоритма обосновывается тем, что с изменением предсказания для одного объекта в зависимости от его класса меняется либо TPR, либо FPR (значение второго параметра остаётся прежним). Ниже описана другая логика, подводящая к алгоритму выше. | ||
| + | |||
| + | [[Файл:ROC_Algo_Alt_Ex1.png|thumb|left|210px|График Accuracy для идеальной классификации]] | ||
| + | [[Файл:ROC_Ex1.png|thumb|right|170px|ROC-кривая для идеальной классификации]] | ||
| + | [[Файл:ROC_Algo_Alt_Ex2.png|thumb|left|210px|График Accuracy для неидеальной классификации]] | ||
| + | [[Файл:ROC_Ex2.png|thumb|right|170px|ROC-кривая для неидеальной классификации]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Напомним, что мы работаем с мягкой классификацией. | ||
| + | |||
| + | Рассмотрим примеры (графики accuracy, цветом указан реальный класс объекта: красный — положительный, синий — отрицательный). | ||
| + | Отсортируем наши объекты по возрастанию уверенности классификатора в принадлежности объекта к положительному классу. Допустим, что объекты находятся на равном (единичном) расстоянии друг от друга. | ||
| + | |||
| + | Начнём перебирать «границу раздела»: если граница в нуле — мы решаем относить все объекты к положительному классу, тогда accuracy = 1/2. | ||
| + | Последовательно сдвигаем границу по единичке вправо: | ||
| + | * если реальный класс объекта, оказавшегося теперь по другую сторону границы — отрицательный, то accuracy увеличивается, так как мы «угадали» класс объекта, решив относить объекты левее границы к отрицательному классу; | ||
| + | * если же реальный класс объекта — положительный, accuracy уменьшается (по той же логике) | ||
| + | |||
| + | Таким образом, на графиках слева, видно, что: | ||
| + | * на графике идеальной классификации точность в 100% достигается, неидеальной — нет; | ||
| + | * площадь под графиком accuracy идеального классификатора больше, чем аналогичная площадь для неидеального. | ||
| + | |||
| + | Заметим, что, повернув график на 45 градусов, мы получим ROC-кривые для соответствующих классификаторов (графикам accuracy слева соответствуют ROC-кривые справа). Так объясняется альтернативный алгоритм построения ROC-кривой. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
= Precision-Recall кривая = | = Precision-Recall кривая = | ||
| Строка 139: | Строка 219: | ||
'''Обоснование: Чувствительность к соотношению классов.''' | '''Обоснование: Чувствительность к соотношению классов.''' | ||
| − | Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм <math>a(x)</math>, идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь | + | Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм <math>a(x)</math>, идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь «плохой» алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. |
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм <math>b(x)</math>, помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95. | Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм <math>b(x)</math>, помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95. | ||
| − | '''Precison-recall (PR) кривая.''' | + | '''Precison-recall (PR) кривая.''' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает '''площадь под PR-кривой''' (англ. '''Area Under the Curve — AUC-PR''') | |
| − | |||
| − | |||
| − | + | = Источники = | |
| − | : | + | * Coursera: https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie |
| − | + | * [[Оценка качества в задачах классификации и регрессии]] | |
| + | * Лекции А. Забашта | ||
| + | * Лекции Е. А. Соколова | ||
| + | * [http://bazhenov.me/blog/2012/07/21/classification-performance-evaluation.html Оценка классификатора (точность, полнота, F-мера)] | ||
Текущая версия на 19:22, 4 сентября 2022
Общие понятия
- TP — true positive: классификатор верно отнёс объект к рассматриваемому классу.
- TN — true negative: классификатор верно утверждает, что объект не принадлежит к рассматриваемому классу.
- FP — false positive: классификатор неверно отнёс объект к рассматриваемому классу.
- FN — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу.
Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное число объектов класса 0 (для бинарного случая 0/1) может выражаться как
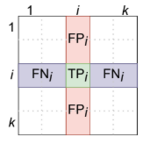
Confusion matrix (матрица ошибок / несоответствий / потерь, CM)
— квадратная матрица размера k × k, где — число объектов класса , которые были квалифицированны как класс , а — число классов. Значения ячеек CM могут быть вычислены по формуле: , где — реальный класс объекта, а — предсказанный.
Для бинарного случая:
| Принадлежит классу (P) | Не принадлежит классу (N) | |
|---|---|---|
| Предсказана принадлежность классу | TP | FP |
| Предсказано отсутствие принадлежности к классу | FN | TN |
Для многоклассовой классификации матрица несоответствий строится по тому же принципу:
| Предсказанный класс | Класс 1 (C₁) | Класс 2 (C₂) | Класс 3 (C₃) |
|---|---|---|---|
| 1 (P₁) | T₁ | F₁₂ | F₁₃ |
| 2 (P₂) | F₂₁ | T₂ | F₂₃ |
| 3 (P₃) | F₃₁ | F₃₂ | T₃ |
В этом случае TP, TN, FP и FN считаются относительно некоторого класса следующим образом:
Простые оценки
- Accuracy — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов.
- Recall — (полнота, sensitivity, TPR (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса.
- Precision — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор.
- Specificity — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно не относит объекты к классу.
- Fall-out — (FPR (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу.
Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации):
- Precision
- Recall
Различные виды агрегации Precision и Recall
Примеры и картинки взяты из лекций курса «Введение в машинное обучение»[1] К.В. Воронцова
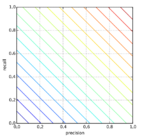
Арифметическое среднее:
- Если precision = 0.05, recall = 1, то A = 0.525
- Если precision = 0.525, recall = 0.525, то A = 0.525.
- Первый классификатор — константный, не имеет смысла.
- Второй классификатор показывает неплохое качество.
Таким образом, взятие среднего арифметического не является показательным.
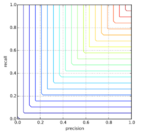
Минимум:
- Если precision = 0.05, recall = 1, то M = 0.05
- Если precision = 0.525, recall = 0.525, то M = 0.525.
То есть, довольно неплохо отражает качество классификатора, не завышая его.
- Если precision = 0.2, recall = 1, то M = 0.2.
- Если precision = 0.2, recall = 0.3, то M = 0.2.
Но не отличает классификаторы с разными неминимальными показателями.
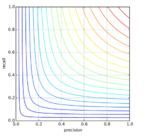
Гармоническое среднее, или F-мера:
- Если precision = 0.05, recall = 1, то F = 0.1.
- Если precision = 0.525, recall = 0.525, то F = 0.525.
- Если precision = 0.2, recall = 1, то F = 0.33.
- Если precision = 0.2, recall = 0.3, то F = 0.24.
Является наиболее точным усреднением, учитывает оба показателя.
Геометрическое среднее, или Индекс Фоулкса–Мэллова (Fowlkes–Mallows index)
Менее строгая мера.
F-мера
Для общей оценки качества классификатора часто используют F₁-меру. Оригинально она вычисляется для позитивного класса случая бинарной классификации, обобщается с помощью приниципа «один против всех» (описан подробнее ниже, для многоклассовой классификации). F₁-мера — среднее гармоническое между precision и recall:
Среднее гармоническое взвешенное Fβ (F1-мера — частный случай Fβ-меры для β = 1). Fβ измеряет эффективность классификатора учитывая recall в β раз более важным чем precision:
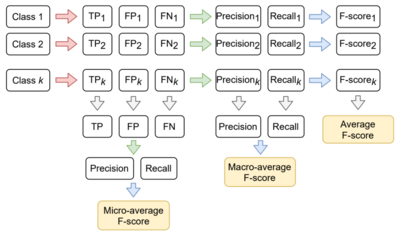
F-мера для многоклассовой классификации. Три вида усреднения
Для вычисления F-меры (и других) метрик в рамках многоклассовой классификации используется подход «один против всех»: каждый класс ровно один раз становится «положительным», а остальные — отрицательным (пример вычисления изображён на матрице).
Таким образом, в зависимости от этапа вычисления, на котором производится усреднение, можно вычислить micro-average, macro-average и average F-меры (логика вычисления изображена на схеме справа). Микро- и макро-:
- ,
где для micro-average precision и recall вычислены из усреднённых TP, FP, FN;
для macro-average precision и recall вычислены из усреднённых precisioni, recalli;
Усреднённая:
- ,
где — индекс класса, а — число классов.
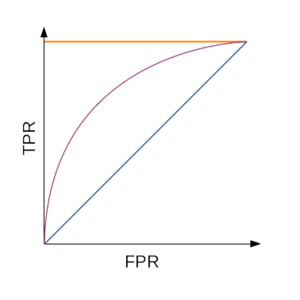
ROC-кривая
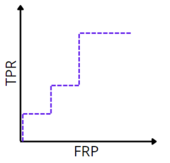
Для наглядной оценки качества алгоритма применяется ROC-кривая. Кривая строится на плоскости, определённой TPR (по оси ординат) и FPR (по оси абсцисс).
Для построении графика используется мягкая классификация: вместо того, чтобы чётко отнести объект к классу, классификатор возвращает вероятности принадлежности объекта к различным классам. Эта уверенность сравнивается с порогом (какой уверенности «достаточно», чтобы отнести объект к положительному классу). В зависимости от значения этого порога меняются значения TPR и FPR.
Алгоритм построения кривой:
- Запустить классификатор на тестовой выборке
- Отсортировать результаты по уверенности классификатора в принадлежности объекта к классу
- Пока не кончились элементы:
- Взять объект с максимальной уверенностью
- Сравнить метку с реальной
- Пересчитать TPR и FPR на взятых объектах
- Поставить точку, если обе характеристики не NaN / ±∞
- Построить кривую по точкам
Таким образом: число точек не превосходит число объектов идеальному алгоритму соответствует ROC-кривая, проходящая через точку худшему алгоритму (например, монетке) соответствует прямая TPR = FPR.
Для численной оценки алгоритма по ROC-кривой используется значение площади под ней (AUC, area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5.
С другой стороны, для построения ROC-кривой не обязательно пересчитывать TPR и FPR.
Существует альтернативный алгоритм построения ROC-кривой.
- сортируем объекты по уверенности классификатора в их принадлежности к положительному классу
- начинаем в точке (0, 0)
- последовательно продолжаем кривую вверх:
- для каждого «отрицательного» объекта вверх
- для каждого «положительного» — вправо.
Корректность алгоритма обосновывается тем, что с изменением предсказания для одного объекта в зависимости от его класса меняется либо TPR, либо FPR (значение второго параметра остаётся прежним). Ниже описана другая логика, подводящая к алгоритму выше.
Напомним, что мы работаем с мягкой классификацией.
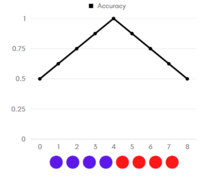
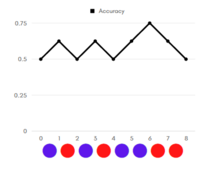
Рассмотрим примеры (графики accuracy, цветом указан реальный класс объекта: красный — положительный, синий — отрицательный). Отсортируем наши объекты по возрастанию уверенности классификатора в принадлежности объекта к положительному классу. Допустим, что объекты находятся на равном (единичном) расстоянии друг от друга.
Начнём перебирать «границу раздела»: если граница в нуле — мы решаем относить все объекты к положительному классу, тогда accuracy = 1/2. Последовательно сдвигаем границу по единичке вправо:
- если реальный класс объекта, оказавшегося теперь по другую сторону границы — отрицательный, то accuracy увеличивается, так как мы «угадали» класс объекта, решив относить объекты левее границы к отрицательному классу;
- если же реальный класс объекта — положительный, accuracy уменьшается (по той же логике)
Таким образом, на графиках слева, видно, что:
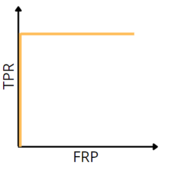
- на графике идеальной классификации точность в 100% достигается, неидеальной — нет;
- площадь под графиком accuracy идеального классификатора больше, чем аналогичная площадь для неидеального.
Заметим, что, повернув график на 45 градусов, мы получим ROC-кривые для соответствующих классификаторов (графикам accuracy слева соответствуют ROC-кривые справа). Так объясняется альтернативный алгоритм построения ROC-кривой.
Precision-Recall кривая
Обоснование: Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь «плохой» алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
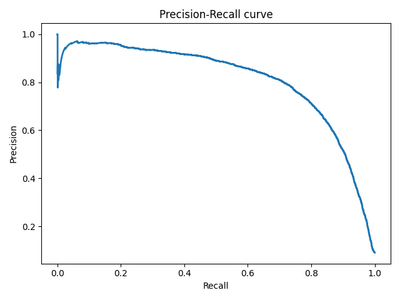
Precison-recall (PR) кривая.
Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
Источники
- Coursera: https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie
- Оценка качества в задачах классификации и регрессии
- Лекции А. Забашта
- Лекции Е. А. Соколова
- Оценка классификатора (точность, полнота, F-мера)