Операции анализа с функциональными рядами — различия между версиями
Smolcoder (обсуждение | вклад) м (→Пункт 2) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 24 промежуточные версии 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == Пункт 1 == | + | [[Равномерная сходимость функционального ряда|<<]] [[Степенные ряды|>>]] |
| + | __TOC__ | ||
| + | |||
| + | == Пункт 1. Коммутируемость суммы и предельного перехода == | ||
Из арифметики пределов функций хорошо известно равенство: | Из арифметики пределов функций хорошо известно равенство: | ||
| − | <tex>\lim \limits_{x \to a} \sum \limits_{k = 0}^{n} f_k(x) = \sum\limits_{k = 0}^{n} \lim \limits_{x \to a} f_k(x)</tex> | + | <tex>\lim \limits_{x \to a} \sum \limits_{k = 0}^{n} f_k(x) = \sum\limits_{k = 0}^{n} \lim \limits_{x \to a} f_k(x)</tex>. |
| + | |||
Возникает вопрос, правда ли, что | Возникает вопрос, правда ли, что | ||
| − | <tex>\lim\limits_{x \to a} \sum\limits_{k = 0}^{\infty} f_k(x) = \sum\limits_{k = 0}^{\infty} \lim\limits_{x \to a} f_k(x)</tex> | + | <tex>\lim\limits_{x \to a} \sum\limits_{k = 0}^{\infty} f_k(x) = \sum\limits_{k = 0}^{\infty} \lim\limits_{x \to a} f_k(x)</tex>? |
| + | |||
Обсуждаемое равенство {{---}} частный случай важного вопроса матанализа, имеющий отношение к перестановке местами | Обсуждаемое равенство {{---}} частный случай важного вопроса матанализа, имеющий отношение к перестановке местами | ||
двух операций предельного перехода, что коротко записывается так: | двух операций предельного перехода, что коротко записывается так: | ||
<tex>\lim \limits_{x \to a} \lim \limits_{y \to b} f(x,y) = \lim \limits_{y \to b} \lim \limits_{x \to a} f(x,y)</tex> | <tex>\lim \limits_{x \to a} \lim \limits_{y \to b} f(x,y) = \lim \limits_{y \to b} \lim \limits_{x \to a} f(x,y)</tex> | ||
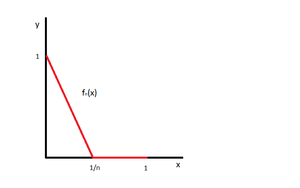
В общем случае это не так. Реанимируем пример, описанный выше и убедимся, что написанное неравенство не верно. | В общем случае это не так. Реанимируем пример, описанный выше и убедимся, что написанное неравенство не верно. | ||
| + | |||
[[file:picture1.png|300px]] | [[file:picture1.png|300px]] | ||
<tex>\lim \limits_{n \to \infty} \lim \limits_{x \to 0} f_n(x) = 1</tex> , так как <tex>\lim \limits_{x \to 0} f_n(x) = 1</tex> | <tex>\lim \limits_{n \to \infty} \lim \limits_{x \to 0} f_n(x) = 1</tex> , так как <tex>\lim \limits_{x \to 0} f_n(x) = 1</tex> | ||
| − | <tex>\lim \limits_{ | + | <tex>\lim \limits_{x \to 0} \lim \limits_{n \to \infty} f_n(x) = 0</tex> , так как <tex>\lim \limits_{n \to \infty} f_n(x) = 0</tex> |
Значит, в данном случае равенство не верно. | Значит, в данном случае равенство не верно. | ||
{{Теорема | {{Теорема | ||
| − | |statement=Пусть на множестве <tex>E</tex> заданы функции <tex>f_n</tex>, <tex> | + | |statement= |
| − | <tex>\forall n \in \mathbb{N} \exists \lim \limits_{x \to a} f_n( | + | Пусть на множестве <tex>E</tex> заданы функции <tex>f_n</tex>, <tex>a</tex> {{---}} предельная точка этого множества и |
| + | <tex>\forall n \in \mathbb{N}\ \exists\ \lim \limits_{x \to a} f_n(x)</tex>. Тогда если <tex>\sum \limits_{n = 0}^{\infty} f_n</tex> - равномерно | ||
сходится на <tex>E</tex>, то выполняется равенство : | сходится на <tex>E</tex>, то выполняется равенство : | ||
| − | <tex>\lim \limits_{x \to a} \sum \limits_{n = 0}^{\infty} = \sum \limits_{n = 0}^{\infty} \ | + | <tex>\lim \limits_{x \to a} \sum \limits_{n = 0}^{\infty} f_n(x) = \sum \limits_{n = 0}^{\infty} \lim\limits_{x \to a} f_n(x)</tex> |
| − | |proof=Пусть <tex>A_n = \lim \limits_{x \to a} f_n(x)</tex>. Прежде всего установим, что <tex>\sum \limits_{n = 1}^{\infty} A_n < + \infty</tex>. | + | |proof= |
| + | Пусть <tex>A_n = \lim \limits_{x \to a} f_n(x)</tex>. Прежде всего установим, что <tex>\sum \limits_{n = 1}^{\infty} A_n < + \infty</tex>. | ||
Так как функциональный ряд сходится равномерно, то по критерию Коши равномерной сходимости: | Так как функциональный ряд сходится равномерно, то по критерию Коши равномерной сходимости: | ||
<tex>\forall \varepsilon > 0 \quad \exists N : \forall m \ge n > N \quad \forall x \in E \Rightarrow |\sum \limits_{k = n}^{m} f_k(x)| \le \varepsilon</tex>. | <tex>\forall \varepsilon > 0 \quad \exists N : \forall m \ge n > N \quad \forall x \in E \Rightarrow |\sum \limits_{k = n}^{m} f_k(x)| \le \varepsilon</tex>. | ||
| Строка 28: | Строка 36: | ||
конечное число слагаемых, то по арифметике пределов можно перейти к пределу при | конечное число слагаемых, то по арифметике пределов можно перейти к пределу при | ||
<tex>x \to a \Rightarrow |\sum \limits_{k = n}^{m} A_k| < \varepsilon</tex>. Здесь <tex>\varepsilon</tex> - произвольно, следовательно по критерию Коши | <tex>x \to a \Rightarrow |\sum \limits_{k = n}^{m} A_k| < \varepsilon</tex>. Здесь <tex>\varepsilon</tex> - произвольно, следовательно по критерию Коши | ||
| − | сходимости числового ряда, этот ряд сходится | + | сходимости числового ряда, этот ряд сходится. |
| − | этого будем использовать введеное ранее понятие остатка ряда, которое без изменения переносится на сходящиеся | + | Докажем теперь равенство из условия. Для этого будем использовать введеное ранее понятие остатка ряда, |
| + | которое без изменения переносится на сходящиеся | ||
функциональные ряды. | функциональные ряды. | ||
<tex>f(x) = \sum \limits_{k = 1}^{\infty} f_k(x)</tex>, <tex>A = \sum \limits_{k = 1}^{\infty} A_k</tex>, | <tex>f(x) = \sum \limits_{k = 1}^{\infty} f_k(x)</tex>, <tex>A = \sum \limits_{k = 1}^{\infty} A_k</tex>, | ||
| − | <tex>f(x) = | + | <tex>f(x) = S_n(x) + R_n(x)</tex> , где <tex>R_n(x) = \sum \limits_{k = n + 1}^{\infty} f_k(x) </tex> |
| − | Аналогично : <tex>A = S_n + R_n</tex>, где <tex>R_n = \sum \limits_{k = n + 1}^{\infty}</tex> | + | Аналогично : <tex>A = S_n + R_n</tex>, где <tex>R_n = \sum \limits_{k = n + 1}^{\infty} A_k </tex> |
Надо доказать, что <tex>\lim \limits_{x \to a} f(x) = A</tex>. Составляем модуль разности : <tex>|f(x) - A| = </tex> | Надо доказать, что <tex>\lim \limits_{x \to a} f(x) = A</tex>. Составляем модуль разности : <tex>|f(x) - A| = </tex> | ||
| − | вставляем остатки <tex>= |S_n(x) + R_n(x) - S_n - R_n| \le |S_n(x) - S_n| + |R_n(x) | + | вставляем остатки <tex>= |S_n(x) + R_n(x) - S_n - R_n| \le |S_n(x) - S_n| + |R_n(x)| + |R_n|</tex> |
В силу сходимости ряда из пределов <tex>R_n \to 0</tex>, а в силу равномерной сходимости функционального ряда | В силу сходимости ряда из пределов <tex>R_n \to 0</tex>, а в силу равномерной сходимости функционального ряда | ||
| − | <tex>R_n \stackrel{E}{\rightrightarrows} 0</tex>. Отсюда ясно, что | + | <tex> R_n(x) \stackrel{E}{\rightrightarrows} 0 </tex>. Отсюда ясно, что |
| − | <tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \quad \forall x \in E \Rightarrow |R_n| < \varepsilon \ | + | <tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \quad \forall x \in E \Rightarrow |R_n| < \varepsilon, \ |R_n(x)| < \varepsilon </tex>. |
| + | |||
Тогда из предыдущего неравенства, подставляя туда <tex>n_0 = N + 1</tex>, | Тогда из предыдущего неравенства, подставляя туда <tex>n_0 = N + 1</tex>, | ||
получаем : <tex>|f(x) - A| \le |S_{n_0}(x) - S_{n_0}| + 2\varepsilon</tex>. Первое слагамое справа состоит из конечного | получаем : <tex>|f(x) - A| \le |S_{n_0}(x) - S_{n_0}| + 2\varepsilon</tex>. Первое слагамое справа состоит из конечного | ||
числа слагаемых, поэтому по арифметике пределов : | числа слагаемых, поэтому по арифметике пределов : | ||
<tex>\lim \limits_{x \to a} S_{n_0}(x) = S_{n_0}</tex>. Значит, для уже существующего | <tex>\lim \limits_{x \to a} S_{n_0}(x) = S_{n_0}</tex>. Значит, для уже существующего | ||
| − | <tex>\varepsilon > 0 \quad \exists \delta > 0 : 0 < |x - | + | <tex>\varepsilon > 0 \quad \exists \delta > 0 : 0 < |x - a| < \delta \Rightarrow |S_{n_0}(x) - S_{n_0}| < \varepsilon</tex>. Финально получаем : |
<tex>\forall \varepsilon > 0 \quad \exists \delta > 0 : 0 < |x - a| < \delta \Rightarrow |f(x) - A| < 3\varepsilon</tex>. | <tex>\forall \varepsilon > 0 \quad \exists \delta > 0 : 0 < |x - a| < \delta \Rightarrow |f(x) - A| < 3\varepsilon</tex>. | ||
Поэтому по определению предела все установлено. | Поэтому по определению предела все установлено. | ||
}} | }} | ||
| − | == Пункт 2 == | + | Следствие из этой теоремы: |
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Равномерно сходящийся на <tex> [a; b] </tex> ряд из непрерывных на этом отрезке функций непрерывен на <tex> [a; b] </tex>. | ||
| + | |proof= | ||
| + | Можно применить только что доказанную теорему к каждой точке <tex> x_0 </tex> из <tex> [a; b] </tex>, полагая <tex> A_n = f_n(x_0) </tex>. | ||
| + | }} | ||
| + | |||
| + | == Пункт 2. Коммутируемость суммы и интеграла == | ||
| + | В этом пункте будет приведено условие, при котором можно записать: | ||
| + | |||
| + | <tex> \int\limits_{a}^{b} \sum\limits_{n = 1}^{\infty} f_{n}(x)dx = | ||
| + | \sum\limits_{n = 1}^{\infty} \int\limits_{a}^{b} f_{n}(x)dx </tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
Заметим, что для суммы конечного числа слагаемых это утверждение верно по линейности интеграла. | Заметим, что для суммы конечного числа слагаемых это утверждение верно по линейности интеграла. | ||
| + | |||
{{Теорема | {{Теорема | ||
| − | |statement= <tex>f_{n} | + | |statement= |
| − | f | + | Пусть <tex> f_{n} </tex> интегрируема и равномерно сходится к <tex> f </tex> на <tex> [a; b] </tex>. Тогда <tex> f </tex> тоже интегрируема, и |
| + | <tex> \lim \limits_{n \to \infty} \int\limits_{a}^{b} f_{n} = \int\limits_{a}^{b}f </tex>. | ||
|proof= | |proof= | ||
| − | 1) Прежде всего установим интегрируемость <tex>f</tex>. Для этого необходимо проверить | + | 1) Прежде всего, установим интегрируемость <tex>f</tex>. Для этого необходимо проверить |
| − | <tex>w(f, \tau) \ | + | <tex>w(f, \tau) \to 0</tex> при <tex>\operatorname{rang} \tau \to 0</tex>. |
| + | |||
По определению, <tex>w(g, [c, d]) = \sup\limits_{x',x'' \in [c,d]} |g(x'') - g(x')|</tex> | По определению, <tex>w(g, [c, d]) = \sup\limits_{x',x'' \in [c,d]} |g(x'') - g(x')|</tex> | ||
<tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \quad \forall x \in [a, b] \quad |f_n(x) - f(x)| < \varepsilon</tex> , что следует из равномерной сходимости. | <tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \quad \forall x \in [a, b] \quad |f_n(x) - f(x)| < \varepsilon</tex> , что следует из равномерной сходимости. | ||
| − | <tex>\forall \tau : a = x_0 < x_1 < | + | <tex>\forall \tau : a = x_0 < x_1 < \dots < x_p = b \quad \forall x', x'' \in [x_k, x_{k+1}] : \\ : |f(x'') - f(x')| \le |f_n(x'') - f_n(x')| + |f_n(x'')-f(x'')| + |f_n(x')-f(x')| \quad \forall n > N</tex> |
В этом случае по выбору <tex>N</tex>, можно написать : | В этом случае по выбору <tex>N</tex>, можно написать : | ||
| − | <tex>|f(x'')-f(x')| | + | <tex>|f(x'') - f(x')| \le |f_n(x'')-f_n(x')| + 2\varepsilon</tex> |
| − | <tex>|f_n(x'')-f_n(x')| | + | <tex>|f_n(x'') - f_n(x')| \le w(f_n, [x_k, x_{k+1}])</tex> |
| − | <tex>f(x'')-f(x') | + | <tex>|f(x'') - f(x')| \le w(f_n, [x_k, x_{k+1}]) + 2\varepsilon</tex> |
В этом неравенстве справа число, переменная есть только слева, поэтому можно перейти к <tex>\sup</tex> по <tex>x', x''</tex>, что | В этом неравенстве справа число, переменная есть только слева, поэтому можно перейти к <tex>\sup</tex> по <tex>x', x''</tex>, что | ||
приводит к неравенству : | приводит к неравенству : | ||
| − | <tex>w(f, [x_k, x_{k+1}]) | + | <tex>w(f, [x_k, x_{k+1}]) \le w(f_n, [x_k, x_{k+1}]) + 2\varepsilon</tex>. |
| + | |||
| + | Это неравенство верно для любого текущего отрезка, лишь бы | ||
выполнялось, что <tex>n > N</tex>. Домножим каждое на <tex>\Delta x_k</tex> и сложим : | выполнялось, что <tex>n > N</tex>. Домножим каждое на <tex>\Delta x_k</tex> и сложим : | ||
| − | <tex>w(f, \tau) | + | <tex>w(f, \tau) \le w(f_{n}, \tau) + 2\varepsilon \underbrace{\sum\limits_{k = 1}^{n - 1}\Delta x_k}_{(b - a)} </tex> |
| − | |||
Подставив в это неравенство <tex>n_0 = N+1</tex>, получим : | Подставив в это неравенство <tex>n_0 = N+1</tex>, получим : | ||
| − | <tex>w(f, \tau) | + | <tex>w(f, \tau) \le w(f_{n_0}, \tau) + 2(b - a)\varepsilon</tex>, функция <tex>f_{n_0} \in \mathcal{R}\left( a, b \right)</tex>. |
| − | Неравенство выполняется для любого <tex>\tau</tex>, значит для уже существующего <tex>\varepsilon | + | |
| − | rang \tau < \delta \Rightarrow w(f_{n_0} < \varepsilon | + | Неравенство выполняется для любого <tex>\tau</tex>, значит для уже существующего разбиения: |
| − | <tex>\varepsilon</tex> - произвольно, отсюда <tex>w(f, \tau) \to 0</tex> при <tex>rang \tau \to 0</tex>. Значит, | + | |
| − | <tex>f \in \mathcal{R}\left ( a, b \right)</tex> | + | <tex>\forall \varepsilon > 0\ \exists \delta > 0 : |
| + | \operatorname{rang} \tau < \delta \Rightarrow w(f_{n_0}, \tau) < \varepsilon \Rightarrow w(f, \tau) < (1 + 2(b - a))\varepsilon</tex>. Здесь | ||
| + | <tex>\varepsilon</tex> - произвольно, отсюда <tex>w(f, \tau) \to 0</tex> при <tex> \operatorname{rang} \tau \to 0</tex>. | ||
| + | |||
| + | Значит, <tex>f \in \mathcal{R}\left ( a, b \right)</tex>. | ||
2) В силу <tex>f_{n} \stackrel{[a, b]}{\rightrightarrows} f \quad \forall \varepsilon > 0 \quad \exists N : \forall n > N | 2) В силу <tex>f_{n} \stackrel{[a, b]}{\rightrightarrows} f \quad \forall \varepsilon > 0 \quad \exists N : \forall n > N | ||
и \forall x \in [a, b] \quad |f_n(x) - f(x)| < \varepsilon</tex> | и \forall x \in [a, b] \quad |f_n(x) - f(x)| < \varepsilon</tex> | ||
| − | |||
| − | <tex>|\int\limits_{a}^{b} f_n - \int\limits_{a}^{b} f| = |\int\ | + | Все функции интегрируемы, в силу этого факта и линейности интеграла можно писать следующее : |
| + | |||
| + | <tex>|\int\limits_{a}^{b} f_n(x) dx - \int\limits_{a}^{b} f(x) dx| = |\int\limits_{a}^{b} (f_n(x) - f(x))dx| \le \int\limits_{a}^{b} |f_n(x) - f(x)| dx \le | ||
(b-a)\varepsilon</tex> | (b-a)\varepsilon</tex> | ||
| − | Таким образом, <tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \Rightarrow |\int\limits_{a}^{b} f_n - \int\limits_{a}^{b} f| | + | Таким образом, <tex>\forall \varepsilon > 0 \quad \exists N : \forall n > N \Rightarrow |\int\limits_{a}^{b} f_n(x) dx - \int\limits_{a}^{b} f(x) dx| \le (b -a)\varepsilon</tex>. |
По определению предела приходим к нужному. | По определению предела приходим к нужному. | ||
}} | }} | ||
| + | |||
| + | Следствие из этой теоремы: | ||
{{Утверждение | {{Утверждение | ||
|statement = | |statement = | ||
| − | Пусть функциональный ряд состоит из <tex>f_n \in \mathcal{R}\left[ a, b \right ]</tex> и равномерно сходится на | + | Пусть функциональный ряд состоит из <tex>f_n \in \mathcal{R}\left[ a, b \right ]</tex> и равномерно сходится на этом отрезке. |
| − | этом отрезке | + | Тогда сумма ряда будет интегрируемой функцией, и будет выполняться: |
<tex>\int\limits_{a}^{b} \sum\limits_{n = 1}^{\infty} f_{n}(x)dx = | <tex>\int\limits_{a}^{b} \sum\limits_{n = 1}^{\infty} f_{n}(x)dx = | ||
| Строка 116: | Строка 145: | ||
}} | }} | ||
| − | ==Пункт 3== | + | ==Пункт 3. Коммутируемость суммы и дифференцирования. == |
| − | Здесь будут установлены условия, при которых можно записать : <tex>(\ | + | Здесь будут установлены условия, при которых можно записать : <tex>(\sum\limits_{n = 1}^{\infty} f_n(x))' = \sum\limits_{n = 1}^{\infty}f_n'(x)</tex> |
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Пусть на <tex> | + | Пусть на <tex> \langle a, b\rangle </tex> задан функциональный ряд <tex>\sum\limits_{n = 1}^{\infty} f_n</tex>, <tex>\exists c \in \langle a, b \rangle, \sum\limits_{n = 1}^{\infty}f_n(c)</tex> - сходится. |
| + | Пусть также <tex>\exists f_n'</tex> - непрерывна на <tex>\langle a, b \rangle</tex> и | ||
<tex>\sum\limits_{n = 1}^{\infty} f_n'</tex> - равномерно сходится на <tex>\langle a, b\rangle</tex>, тогда на <tex>\langle a, b \rangle</tex> выполняется : | <tex>\sum\limits_{n = 1}^{\infty} f_n'</tex> - равномерно сходится на <tex>\langle a, b\rangle</tex>, тогда на <tex>\langle a, b \rangle</tex> выполняется : | ||
| − | <tex>(\ | + | <tex>(\sum\limits_{n = 1}^{\infty} f_n(x))' = \sum\limits_{n = 1}^{\infty}f_n'(x)</tex>. |
|proof= | |proof= | ||
| − | Пусть <tex>g(x) = \sum\limits_{n = 1}^{\infty}f_n'(x)</tex>. | + | Пусть <tex>g(x) = \sum\limits_{n = 1}^{\infty}f_n'(x)</tex>. |
| − | |||
| − | <tex> | + | Ряд из <tex>f_n'</tex> - равномерно сходится, следовательно <tex>g</tex> непрерывна на <tex>\langle a, b \rangle </tex>, тогда по теореме о почленном интегрировании функцию можно записать в виде: |
| − | \ | ||
| − | Так как <tex>\sum\limits_{n = 1}^{\infty}f_n(c)</tex> - сходится, а <tex>\sum\limits_{n = 1}^{\infty}(f_n(x)-f_n(c))</tex> - | + | <tex> \int\limits_{c}^{x}g(t)dt = \sum\limits_{n = 1}^{\infty} \int\limits_{c}^{x}f_n'(t)dt = |
| − | сходится по последнему равенству, то по линейности рядов записав <tex>f_n(x)=(f_n(x)-f_n( | + | \sum\limits_{n=1}^{\infty}(f_n(x)-f_n(c)) </tex> |
| + | |||
| + | Так как <tex>\sum\limits_{n = 1}^{\infty}f_n(c)</tex> - сходится, а <tex>\sum\limits_{n = 1}^{\infty}(f_n(x) - f_n(c))</tex> - | ||
| + | сходится по последнему равенству, то по линейности рядов, записав <tex>f_n(x)=(f_n(x) - f_n(c)) + f_n(c)</tex>, получим, что | ||
<tex>\sum\limits_{n = 1}^{\infty}f_n(x)</tex> - сходится. Для всех <tex>f(x)</tex> получаем | <tex>\sum\limits_{n = 1}^{\infty}f_n(x)</tex> - сходится. Для всех <tex>f(x)</tex> получаем | ||
<tex>\int\limits_{c}^{x}g(t)dt = f(x)-\sum\limits_{n = 1}^{\infty}f_n(c)</tex> | <tex>\int\limits_{c}^{x}g(t)dt = f(x)-\sum\limits_{n = 1}^{\infty}f_n(c)</tex> | ||
| − | Функция слева дифференцируема, тогда по теореме Барроу, | + | Функция слева дифференцируема, тогда, по теореме Барроу, производная есть у функции справа : <tex>g(x) = f'(x)</tex>, что совпадает с тем, что надо было доказать. |
| − | совпадает с тем, что надо было доказать. | ||
}} | }} | ||
| + | |||
| + | [[Равномерная сходимость функционального ряда|<<]] [[Степенные ряды|>>]] | ||
| + | [[Категория:Математический анализ 1 курс]] | ||
Текущая версия на 19:41, 4 сентября 2022
Содержание
Пункт 1. Коммутируемость суммы и предельного перехода
Из арифметики пределов функций хорошо известно равенство: .
Возникает вопрос, правда ли, что ?
Обсуждаемое равенство — частный случай важного вопроса матанализа, имеющий отношение к перестановке местами двух операций предельного перехода, что коротко записывается так: В общем случае это не так. Реанимируем пример, описанный выше и убедимся, что написанное неравенство не верно.
, так как
, так как
Значит, в данном случае равенство не верно.
| Теорема: |
Пусть на множестве заданы функции , — предельная точка этого множества и
. Тогда если - равномерно сходится на , то выполняется равенство : |
| Доказательство: |
|
Пусть . Прежде всего установим, что . Так как функциональный ряд сходится равномерно, то по критерию Коши равномерной сходимости: . Так как написанное неравенство выполняется для , а под знаком модуля стоит конечное число слагаемых, то по арифметике пределов можно перейти к пределу при . Здесь - произвольно, следовательно по критерию Коши сходимости числового ряда, этот ряд сходится. Докажем теперь равенство из условия. Для этого будем использовать введеное ранее понятие остатка ряда, которое без изменения переносится на сходящиеся функциональные ряды. , , , где Аналогично : , где Надо доказать, что . Составляем модуль разности : вставляем остатки В силу сходимости ряда из пределов , а в силу равномерной сходимости функционального ряда . Отсюда ясно, что . Тогда из предыдущего неравенства, подставляя туда , получаем : . Первое слагамое справа состоит из конечного числа слагаемых, поэтому по арифметике пределов : . Значит, для уже существующего . Финально получаем : . Поэтому по определению предела все установлено. |
Следствие из этой теоремы:
| Утверждение: |
Равномерно сходящийся на ряд из непрерывных на этом отрезке функций непрерывен на . |
| Можно применить только что доказанную теорему к каждой точке из , полагая . |
Пункт 2. Коммутируемость суммы и интеграла
В этом пункте будет приведено условие, при котором можно записать:
Заметим, что для суммы конечного числа слагаемых это утверждение верно по линейности интеграла.
| Теорема: |
Пусть интегрируема и равномерно сходится к на . Тогда тоже интегрируема, и
. |
| Доказательство: |
|
1) Прежде всего, установим интегрируемость . Для этого необходимо проверить при . По определению, , что следует из равномерной сходимости. В этом случае по выбору , можно написать :
В этом неравенстве справа число, переменная есть только слева, поэтому можно перейти к по , что приводит к неравенству : . Это неравенство верно для любого текущего отрезка, лишь бы выполнялось, что . Домножим каждое на и сложим :
Подставив в это неравенство , получим : , функция . Неравенство выполняется для любого , значит для уже существующего разбиения: . Здесь - произвольно, отсюда при . Значит, . 2) В силу Все функции интегрируемы, в силу этого факта и линейности интеграла можно писать следующее :
Таким образом, . По определению предела приходим к нужному. |
Следствие из этой теоремы:
| Утверждение: |
Пусть функциональный ряд состоит из и равномерно сходится на этом отрезке.
Тогда сумма ряда будет интегрируемой функцией, и будет выполняться: |
| Для доказательства в качестве в теореме необходимо использовать частичные суммы функционального ряда. |
Пункт 3. Коммутируемость суммы и дифференцирования.
Здесь будут установлены условия, при которых можно записать :
| Теорема: |
Пусть на задан функциональный ряд , - сходится.
Пусть также - непрерывна на и - равномерно сходится на , тогда на выполняется : . |
| Доказательство: |
|
Пусть . Ряд из - равномерно сходится, следовательно непрерывна на , тогда по теореме о почленном интегрировании функцию можно записать в виде:
Так как - сходится, а - сходится по последнему равенству, то по линейности рядов, записав , получим, что - сходится. Для всех получаем Функция слева дифференцируема, тогда, по теореме Барроу, производная есть у функции справа : , что совпадает с тем, что надо было доказать. |