О замене переменной в интеграле многих переменных — различия между версиями
Sementry (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 6 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
Как обычно, будем рассматривать функцию двух переменных. | Как обычно, будем рассматривать функцию двух переменных. | ||
| Строка 17: | Строка 15: | ||
<tex>\frac{\Delta S}{\Delta\alpha\Delta r} = r + \frac12\Delta r</tex> | <tex>\frac{\Delta S}{\Delta\alpha\Delta r} = r + \frac12\Delta r</tex> | ||
| − | <tex>\Delta \alpha, \Delta r \to 0 \Rightarrow \frac{\Delta S}{\Delta\alpha \Delta r} \to | + | <tex>\Delta \alpha, \Delta r \to 0 \Rightarrow \frac{\Delta S}{\Delta\alpha \Delta r} \to r</tex> |
Или, <tex>\Delta S \approx r\Delta\alpha\Delta r</tex>. | Или, <tex>\Delta S \approx r\Delta\alpha\Delta r</tex>. | ||
| Строка 58: | Строка 56: | ||
КАРТИНКА[<tex> P \in E_P </tex> преобразованием T переходит в <tex> P' \in E_P' </tex>] | КАРТИНКА[<tex> P \in E_P </tex> преобразованием T переходит в <tex> P' \in E_P' </tex>] | ||
| − | <tex>\forall\varepsilon > 0\ \exists \delta > 0 : \operatorname{diam} E_P < \delta \Rightarrow \left|\frac{|E_p|}{|E'_P|} - r \right| < \varepsilon</tex> | + | <tex>\forall\varepsilon > 0\ \exists \delta > 0 : \operatorname{diam} E_P < \delta \Rightarrow \left|\frac{|E_p|}{|E'_P|} - r \right| < \varepsilon, \forall P \subset \Pi</tex> |
| − | Рассмотрим квадрируемую фигуру <tex>E</tex>. <tex>E = \bigcup\limits_{j = 1}^p E_j</tex>, <tex>|E| = \sum\limits_{j = 1}^p |E_j|</tex> | + | Рассмотрим квадрируемую фигуру <tex>E</tex>. <tex>E = \bigcup\limits_{j = 1}^p E_j</tex>; |
| + | <tex>E_i \cap E_j = \varnothing, \forall i \ne j</tex>; | ||
| + | <tex>|E| = \sum\limits_{j = 1}^p |E_j|</tex> | ||
<tex>|E_j| = r_j|E'_j| + \alpha_j |E'_j|</tex>, где <tex>\alpha_j</tex> {{---}} бесконечно малое. | <tex>|E_j| = r_j|E'_j| + \alpha_j |E'_j|</tex>, где <tex>\alpha_j</tex> {{---}} бесконечно малое. | ||
| Строка 71: | Строка 71: | ||
Тогда первое слагаемое {{---}} интегральная сумма, а второе стремится к нулю. Тогда | Тогда первое слагаемое {{---}} интегральная сумма, а второе стремится к нулю. Тогда | ||
| − | <tex>E = \iint\limits_{E'}rd\alpha dr + 0 = \iint\limits_{E'} rd\alpha dr</tex> | + | <tex>|E| = \iint\limits_{E'}rd\alpha dr + 0 = \iint\limits_{E'} rd\alpha dr</tex> |
Пример. | Пример. | ||
| Строка 98: | Строка 98: | ||
В $OXY$ элементарная клетка {{---}} прямоугольник. | В $OXY$ элементарная клетка {{---}} прямоугольник. | ||
| − | + | <tex dpi =150>\frac{|E_{uv}|}{|E'_{uv}|} = \frac{|E_{uv}|}{\Delta u\Delta v}</tex> | |
Соединим отрезками вершины клетки, получим четырёхугольник, который примерно параллелограмм, и вычислим его площадь. | Соединим отрезками вершины клетки, получим четырёхугольник, который примерно параллелограмм, и вычислим его площадь. | ||
| Строка 104: | Строка 104: | ||
Можно действовать по-другому: построить касательные к линиям уровня в точках пересечения, нормировать их, получить паралелограмм и считать его площадь. | Можно действовать по-другому: построить касательные к линиям уровня в точках пересечения, нормировать их, получить паралелограмм и считать его площадь. | ||
| − | Эти попытки связаны с тем, что хочется понять, что будет аналогом | + | Эти попытки связаны с тем, что хочется понять, что в общем случае будет аналогом коэффициентом <tex>r</tex> в полярных координатах. |
| + | |||
| + | <tex> K_u</tex> - касательные. | ||
$\overline K_u = (x_v'; y_v')$ {{---}} касательный вектор к линии уровня $l_u$ | $\overline K_u = (x_v'; y_v')$ {{---}} касательный вектор к линии уровня $l_u$ | ||
| Строка 122: | Строка 124: | ||
$ S = |J(u, v)|\Delta u \Delta v$. | $ S = |J(u, v)|\Delta u \Delta v$. | ||
| − | Для $p \in E_p$, $\frac{|E_p|}{|E_p'|} \xrightarrow[diam | + | Для $p \in E_p$, $\frac{|E_p|}{|E_p'|} \xrightarrow[diam E'_p \rightarrow 0]{}{|J(u, v)|}$, получившийся предел называется якобианом преобразования. |
В итоге получаем $|E| = \iint\limits_{E}dxdy = \iint\limits_{E'}|J(u, v)|dudv$ | В итоге получаем $|E| = \iint\limits_{E}dxdy = \iint\limits_{E'}|J(u, v)|dudv$ | ||
<Сюда можно впилить долгий монолог о сложности понятия площади поверхности> | <Сюда можно впилить долгий монолог о сложности понятия площади поверхности> | ||
| + | Собственно вот он: | ||
| + | Анри Картан - плоскость - линейное многообразие(Подход снимает вопрос образа триангуляции) | ||
| + | |||
| + | <tex>S \begin {cases} | ||
| + | x &= x(u, v)\\ | ||
| + | y &= y(u, v)\\ | ||
| + | z &= z(u, v)\\ | ||
| + | \end {cases} </tex> | ||
| + | <tex>(u,v) \in E \subset \mathbb R</tex> | ||
| + | Площадь <tex>S \stackrel{def}= \iint\limits_{E} \sqrt{(\frac{D(x; y)}{D(u;v)})^2+(\frac{D(x; z)}{D(u;v)})^2+(\frac{D(y; z)}{D(u;v)})}^2dudv=</tex> | ||
| + | <tex>=\iint\limits_{E'}|J(u, v)|dudv</tex>; где <tex>\frac{D(x,y)}{D(u,v)}=\begin {vmatrix} | ||
| + | x_u' & x_v' \\ | ||
| + | y_u' & y_v' \\ | ||
| + | \end {vmatrix} | ||
| + | </tex> | ||
| + | |||
{{Теорема | {{Теорема | ||
| Строка 151: | Строка 169: | ||
$E$ - квадрируема, значит, сумма площадей параллелограммов(а в образе - прямоугольников) на границе будет сколь угодно малой при устремлении ранга разбиения к нулю. Значит, можно принебречь суммой этих групп слагаемых в соответствующих интегральных суммах. | $E$ - квадрируема, значит, сумма площадей параллелограммов(а в образе - прямоугольников) на границе будет сколь угодно малой при устремлении ранга разбиения к нулю. Значит, можно принебречь суммой этих групп слагаемых в соответствующих интегральных суммах. | ||
| − | Рассмотрим кусочек интегральной суммы, $f(p_i)|E_i| | + | Рассмотрим кусочек интегральной суммы, $f(p_i)|E_i|$. Как мы ранее установили, $|E_i| = \iint\limits{E_i'}|J(u, v)|dudv$. |
| − | Пусть | + | Пусть <tex>p_i=(x_i, y_i)</tex>,<tex>p_i'=(u_i,v_i)</tex>, |
| + | <tex>\begin{cases} | ||
| + | x_i & = x_i(u_i, v_i)\\ | ||
| + | y_i & = y_i(u_i, v_i)\\ | ||
| + | \end{cases}</tex>; | ||
| + | <tex>p_i'</tex>-образ точки <tex>p_i</tex>/ | ||
| + | Если писать интегральные суммы для образа, то текущее слагаемоеЖ | ||
| − | $ | + | $f(x(u_i, v_i), y(u_i, v_i)) |J(u_i, v_i)|\Delta u_i \Delta v_i$. |
| − | Сравним с | + | Сравним с 2 слагаемых: |
| − | + | <tex>| f(x_i, y_i)||E_i| - f(x(u_i, v_i), y(u_i, v_i)) |J(u_i, v_i)|\Delta u_i \Delta v_i | =</tex> | |
| − | + | <tex>= |f(x_i, y_i)| \iint \limits_{E_i'}|J(u, v)|dudv - |J(u_i, v_i)|\Delta u_i \Delta v_i | \le</tex> | |
| − | (так как | + | (так как $\Delta u_i \Delta v_i = \iint\limits_{E_i'}dudv$.) |
| + | Преобразование координат гладкое <tex> \Rightarrow </tex><tex>J</tex> - непрерывная функция; всё множество компактно <tex>\Rightarrow</tex> <tex>f</tex> равномерно непрерывна <tex>\Rightarrow </tex> | ||
| + | <tex>rang~ \tau < \delta, \forall E_i' ||J(u, v)|-|J(u_i, v_i)|| \le \varepsilon \Rightarrow </tex> | ||
| − | $\le f(x_i, y_i) \iint\ | + | $\le f(x_i, y_i) \iint\limits_{E_i'} \left| |J(u, v)| - |J(u_i, v_i)| \right|dudv \le$ |
| − | ( | + | <tex>\iint \limits_{E_i'}||J(u, v)| - |J(u_i, v_i)||\Delta u_i \Delta v_i | \le</tex> |
| − | $\le \varepsilon | | + | $\le \varepsilon |E_i'|$ |
| − | Это выполняется для любого $\varepsilon > 0$, значит, теорема доказана. | + | Тогда для интеграла по всей $E$ имеем: |
| + | |||
| + | $\left| \sum\limits_{i=1}^n f(p_i)|E_i| - \sum\limits_{i=1}^n f(x(u_i, v_i), y(u_i, v_i)) |J(u_i, v_i)|\Delta u_i \Delta v_i \right| \le $ | ||
| + | |||
| + | $ \le \varepsilon \sum\limits_{i=1}^n |E'_i| = \varepsilon \sum\limits_{i=1}^n |E'| $. | ||
| + | |||
| + | Это выполняется для любого $\varepsilon > 0$, значит в пределе <tex>\iint\limits_{E}f(x, y)dxdy = \iint\limits_{E'}f(x(u, v), y(u, v))|J(u, v)|dudv</tex>, а следовательно теорема доказана. | ||
}} | }} | ||
| − | + | В теории интеграла Лебега будет установлена более общая теорема(Фубини) | |
</wikitex> | </wikitex> | ||
| + | |||
| + | [[Категория:Математический анализ 1 курс]] | ||
Текущая версия на 19:07, 4 сентября 2022
Как обычно, будем рассматривать функцию двух переменных.
[Тут какое-то невнятно написанное предложение про мотивацию]
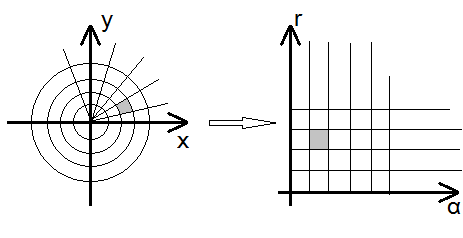
Площадь сектора . Пусть эта формула нам известна. (рис 1)
КАРТИНКА КАРТИНКА[Окружности радиуса и с общим центром. Также нарисован угол , площать - площадь сегмента, окраниченного двумя окружностями и углом.]
,
Или, .
Рассмотрим полярные координаты.
Рассмотрим линии уровня. — ГМТ, для каждой из которых значение радиуса одно и то же и равно . Аналогично, — ГМТ, для каждой из которых
Меняя в и и , покрываем плоскость сетью окружностей и лучей.
Если на написанную систему соотношений смотреть как на преобразование плоскости и смотреть образы и , в силу их определений это будет сеть вертикалей и горизонталей.
Если заштриховать фигуру, границы которой — эти линии, то её образ будет прямоугольником. При обозначении его площади за получаем предел выше. Тогда этот предел — коэффициент искажения элементарной площади при переходе из одной системы осей в другую.
Прямоугольник под действим переходит в , причём ().
Итак, первый этап завершён. Найдена плотность(коэффициент искажения).
На втором этапе мы заинтегрируем эту плотность и придём к формуле , которая будет базовой формулой для того, что бы научиться заменять переменные в двойных интегралах.
Будем считать, что мы знаем, что если есть , — образ, то , где . Это стремление равномерно по положению точки в пределах прямоугольника. (рис 5)
КАРТИНКА[ преобразованием T переходит в ]
Рассмотрим квадрируемую фигуру . ;
;
, где — бесконечно малое.
По равномерной непрерывности, при , .
Тогда первое слагаемое — интегральная сумма, а второе стремится к нулю. Тогда
Пример. КАРТИНКА[Круг под действием преобразования переходит в прямоугольник.]
Плошадь круга.
Общий случай
<wikitex> Пусть $\begin{cases} x & = x(u, v)\\ y & = y(u, v)\\ \end{cases}$;
где $(x, y)$ — прямоугольные координаты, $(u, v)$ — криволинейные.
$l_u$, $l_v$ — линии уровня(координатные линии) в $OXY$.
КАРТИНКА КАРТИНКА[Кривые линии уровня и переход их под действием преобразования в стандартные линии уровня для плоскости.]
Рассмотрим элементарную клетку получвшейся криволинейной сети.
КАРТИНКА КАРТИНКА[в безобразии из предыдущей пары картинок рассматриваем элементарную клетку $E_{uv}$, зажатую между соседними линиями]
В $OXY$ элементарная клетка — прямоугольник.
Соединим отрезками вершины клетки, получим четырёхугольник, который примерно параллелограмм, и вычислим его площадь.
Можно действовать по-другому: построить касательные к линиям уровня в точках пересечения, нормировать их, получить паралелограмм и считать его площадь.
Эти попытки связаны с тем, что хочется понять, что в общем случае будет аналогом коэффициентом в полярных координатах.
- касательные.
$\overline K_u = (x_v'; y_v')$ — касательный вектор к линии уровня $l_u$
$\overline K_v = (x_u'; y_u')$ — касательный вектор к линии уровня $l_v$
$K_u\Delta v, K_v\Delta u$ - элементарные приращения, приблизительно образующие $E_{uv}$. Построим на них параллелограмм, его площадь:
$P(u, v) = \begin{pmatrix} x_u' & y_u' \\ x_v' & y_v' \\ \end{pmatrix} $
$J(u, v) = det(P(u, v))$;
$ S = |J(u, v)|\Delta u \Delta v$.
Для $p \in E_p$, $\frac{|E_p|}{|E_p'|} \xrightarrow[diam E'_p \rightarrow 0]{}{|J(u, v)|}$, получившийся предел называется якобианом преобразования.
В итоге получаем $|E| = \iint\limits_{E}dxdy = \iint\limits_{E'}|J(u, v)|dudv$
<Сюда можно впилить долгий монолог о сложности понятия площади поверхности> Собственно вот он: Анри Картан - плоскость - линейное многообразие(Подход снимает вопрос образа триангуляции)
Площадь ; где
| Теорема (Замена переменных интегрирования в двойном интеграле): |
Пусть дан закон преобразования переменных,
$\begin{cases} x & = x(u, v)\\ y & = y(u, v)\\ \end{cases}$; $E$ - квадрируемая фигура в $Oxy$, якобиан преобразования определен так же, как и ранее. Пусть $f: E \rightarrow \mathbb R$. Тогда выполняется $ |
| Доказательство: |
|
Если всё делать строго, мы утонем в некоторой дифференицальной геометрии. Будем всё делать нестрого. Покроем плоскость сетью координатных линий с малыми шагами, в результате $E$ будет разбиваться на части элементарными криволинейными параллелограммами. Перейдем к образу: КАРТИНКА КАРТИНКА[переход к образу, все так же, как и для фигуры Е ранее] Каждая прямоугольная клетка справа является образом элементарного криволинейного параллелограмма слева. $E$ - квадрируема, значит, сумма площадей параллелограммов(а в образе - прямоугольников) на границе будет сколь угодно малой при устремлении ранга разбиения к нулю. Значит, можно принебречь суммой этих групп слагаемых в соответствующих интегральных суммах. Рассмотрим кусочек интегральной суммы, $f(p_i) |
В теории интеграла Лебега будет установлена более общая теорема(Фубини) </wikitex>