Поиск с помощью золотого сечения — различия между версиями
(Новая страница: «{{В разработке}} '''Поиск с помощью золотого сечения''' (''Golden section search'') - это улучшение наивной…») |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 54 промежуточные версии 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Поиск с помощью золотого сечения''' (англ. ''Golden section search'') {{---}} это улучшение наивной реализации [[Троичный поиск|троичного поиска]], служащего для нахождения минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации). | |
| − | '''Поиск с помощью золотого сечения''' (''Golden section search'') - это улучшение наивной реализации троичного поиска, | ||
==Алгоритм== | ==Алгоритм== | ||
| − | + | ===Обоснование=== | |
| + | Рассмотрим одну итерацию алгоритма [[Троичный поиск|троичного поиска]]. Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана. | ||
| + | |||
| + | [[Файл:new_seg.gif|right|450px|Старая точка x1 уже делит отрезок в нужном отношении, поэтому нет необходимости вычислять ее заново (красным отмечены новые значения точек).]] | ||
| + | |||
| + | Для этого нам потребуется, чтобы одновременно выполнялись равенства: | ||
| + | |||
| + | <tex> \dfrac{a + b}{c} = \dfrac{b + c}{a} = \varphi </tex> | ||
| + | |||
| + | Расстояние от <tex>l</tex> до <tex>x1 = a + b - c = a' </tex>, от <tex>x2 </tex> до <tex> r = b = c'</tex>, от <tex>х1 </tex> до <tex> х2 = c - b = b'</tex>. Т.е. если мы подставим <tex>a', b', c'</tex> в старое соотношение <tex> \dfrac{a + b}{c} </tex>, то получится <tex> \dfrac {a + b - c + c - b}{b} = \dfrac{a}{b}</tex>. | ||
| + | |||
| + | <tex> \dfrac{a}{b} = \varphi </tex> | ||
| + | |||
| + | <tex> \dfrac{c}{b} = \varphi </tex> | ||
| + | |||
| + | Где <tex> \varphi </tex> {{---}} это некоторое отношение, в котором мы делим отрезок (точки <tex>x_1</tex> и <tex>x_2</tex> разбивают отрезок симметрично). | ||
| + | |||
| + | Тогда: | ||
| + | |||
| + | <tex> a + b = \varphi c, a = \varphi b, c = \varphi b</tex>, откуда получаем <tex> \varphi + 1 = \varphi^2 \Rightarrow \varphi = \dfrac{1 + \sqrt{5}}{2}</tex> (тот корень уравнения, который меньше нуля, по понятным причинам отбросили). | ||
| + | |||
| + | Это число совпадает с золотым сечением. Отсюда название метода. | ||
| + | |||
| + | ===Свойства золотого сечения=== | ||
| + | Для реализации алгоритма нам потребуется найти <tex> a </tex> и <tex> a + b </tex>. Если <tex> L </tex> {{---}} длина исследуемого отрезка, тогда: | ||
| + | |||
| + | <tex> \left(\dfrac{b + c}{a} = \varphi;\; b + c = L - a \right) \Rightarrow</tex> | ||
| + | |||
| + | <tex> a = \dfrac{L}{\varphi + 1} </tex> | ||
| + | |||
| + | <tex> a + b = L - c = L - a = L - \dfrac{L}{\varphi + 1}</tex> | ||
| + | |||
| + | Заметим, что в силу того, что <tex>\varphi</tex> {{---}} золотое сечение, то <tex>\dfrac{1}{\varphi + 1} = 2 - \varphi</tex>. | ||
| + | |||
| + | ===Итоговый алгоритм выбора границ=== | ||
| + | Формально для поиска минимума (для максимума {{---}} делается аналогично) функции <tex> f </tex> делаем следующее: | ||
| + | |||
| + | :'''Шаг 1''': | ||
| + | ::Определяем границы поиска <tex>l</tex> и <tex>r</tex>, затем устанавливаем текущее разбиение: | ||
| + | ::<tex>x_1 = l + \dfrac{r - l}{\varphi + 1}</tex> | ||
| + | ::<tex>x_2 = r - \dfrac{r - l}{\varphi + 1}</tex> | ||
| + | ::и вычислим функцию на них: <tex>f_1 = f(x_1), f_2 = f(x_2)</tex> | ||
| + | |||
| + | :'''Шаг 2''': | ||
| + | :: если <tex>f_1 < f_2</tex>, тогда | ||
| + | ::: <tex>r = x_2</tex> | ||
| + | ::: <tex>x_2 = x_1, f_2 = f_1</tex> | ||
| + | ::: <tex>x_1 = l + \dfrac{r - l}{\varphi + 1},\; f_1 = f(x_1)</tex> | ||
| + | :: иначе: | ||
| + | ::: <tex>l = x_1</tex> | ||
| + | ::: <tex>x_1 = x_2, f_1 = f_2</tex> | ||
| + | ::: <tex>x_2 = r - \dfrac{r - l}{\varphi + 1},\; f_2 = f(x_2)</tex> | ||
| + | :'''Шаг 3''': | ||
| + | :: если точность <tex>|r - l| < \varepsilon</tex> нас устраивает, тогда останавливаемся, и искомая точка <tex>x = \dfrac{l + r}{2}</tex>, иначе назад к шагу 2 | ||
| + | |||
===Псевдокод=== | ===Псевдокод=== | ||
| + | '''double''' goldenSectionSearch(f: '''double -> double''', l: '''double''', r: '''double''', eps: '''double'''): | ||
| + | phi = (1 + sqrt(5)) / 2 | ||
| + | resphi = 2 - phi | ||
| + | x1 = l + resphi * (r - l) | ||
| + | x2 = r - resphi * (r - l) | ||
| + | f1 = f(x1) | ||
| + | f2 = f(x2) | ||
| + | '''do''' | ||
| + | '''if''' f1 < f2 | ||
| + | r = x2 | ||
| + | x2 = x1 | ||
| + | f2 = f1 | ||
| + | x1 = l + resphi * (r - l) | ||
| + | f1 = f(x1) | ||
| + | '''else''' | ||
| + | l = x1 | ||
| + | x1 = x2 | ||
| + | f1 = f2 | ||
| + | x2 = r - resphi * (r - l) | ||
| + | f2 = f(x2) | ||
| + | '''while''' abs(r - l) < eps | ||
| + | '''return''' (x1 + x2) / 2 | ||
| + | |||
| + | ===Ошибки псевдокода=== | ||
| + | 1. Используются вычислительно-неустойчивые формулы. | ||
| + | 2. Учитывается только абсолютная длина отрезка. | ||
| + | Подробнее: | ||
| + | http://mech.math.msu.su/~iliagri/zip/sem2book.pdf | ||
| + | |||
| + | ==Время работы== | ||
| + | Так как на каждой итерации мы считаем одно значение функции и уменьшаем область поиска в <tex> \varphi </tex> раз, пока <tex> r - l > \varepsilon</tex>, | ||
| + | то время работы алгоритма составит | ||
| + | <tex> \log_{\varphi}\left(\dfrac{r - l}{\varepsilon}\right)</tex>. | ||
| + | |||
| + | Если удельный вес вычисления функции <tex> f </tex> достаточно большой, тогда получим ускорение работы по сравнению с неулучшенным [[Троичный поиск|троичным поиском]] (<tex> \log_{\varphi}\left(\dfrac{r - l}{\varepsilon}\right)</tex> против <tex>2 \log_{\frac32} \left(\dfrac{r - l}{\varepsilon}\right)</tex>. | ||
| + | За счет этого достигается выигрыш в производительности, т.к. каждый новый отрезок в <tex>\approx 1.618 </tex> раз короче предыдущего (против <tex>1.5</tex> у троичного поиска) и сходится он в <tex>\log_{\frac32} \left(\dfrac{1 + \sqrt{5}}{2}\right) \approx 1.1868 </tex> быстрее, чем в троичном поиске, соответственно, в <tex> \approx 2.3736 </tex> раза меньше вычислений. | ||
| − | == | + | ==См также== |
| + | *[[Троичный поиск]] | ||
| + | *[[Целочисленный двоичный поиск]] | ||
| + | ==Источники информации== | ||
| + | *[http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B7%D0%BE%D0%BB%D0%BE%D1%82%D0%BE%D0%B3%D0%BE_%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F Википедия {{---}} Метод золотого сечения] | ||
| + | *[http://en.wikipedia.org/wiki/Golden_section_search Wikipedia {{---}} Golden section search] | ||
| − | + | [[Категория:Дискретная математика и алгоритмы]] | |
| − | [ | + | [[Категория:Алгоритмы поиска]] |
Текущая версия на 19:05, 4 сентября 2022
Поиск с помощью золотого сечения (англ. Golden section search) — это улучшение наивной реализации троичного поиска, служащего для нахождения минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации).
Алгоритм
Обоснование
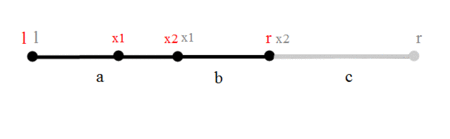
Рассмотрим одну итерацию алгоритма троичного поиска. Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана.
Для этого нам потребуется, чтобы одновременно выполнялись равенства:
Расстояние от до , от до , от до . Т.е. если мы подставим в старое соотношение , то получится .
Где — это некоторое отношение, в котором мы делим отрезок (точки и разбивают отрезок симметрично).
Тогда:
, откуда получаем (тот корень уравнения, который меньше нуля, по понятным причинам отбросили).
Это число совпадает с золотым сечением. Отсюда название метода.
Свойства золотого сечения
Для реализации алгоритма нам потребуется найти и . Если — длина исследуемого отрезка, тогда:
Заметим, что в силу того, что — золотое сечение, то .
Итоговый алгоритм выбора границ
Формально для поиска минимума (для максимума — делается аналогично) функции делаем следующее:
- Шаг 1:
- Определяем границы поиска и , затем устанавливаем текущее разбиение:
- и вычислим функцию на них:
- Шаг 2:
- если , тогда
- иначе:
- если , тогда
- Шаг 3:
- если точность нас устраивает, тогда останавливаемся, и искомая точка , иначе назад к шагу 2
Псевдокод
double goldenSectionSearch(f: double -> double, l: double, r: double, eps: double):
phi = (1 + sqrt(5)) / 2
resphi = 2 - phi
x1 = l + resphi * (r - l)
x2 = r - resphi * (r - l)
f1 = f(x1)
f2 = f(x2)
do
if f1 < f2
r = x2
x2 = x1
f2 = f1
x1 = l + resphi * (r - l)
f1 = f(x1)
else
l = x1
x1 = x2
f1 = f2
x2 = r - resphi * (r - l)
f2 = f(x2)
while abs(r - l) < eps
return (x1 + x2) / 2
Ошибки псевдокода
1. Используются вычислительно-неустойчивые формулы. 2. Учитывается только абсолютная длина отрезка. Подробнее: http://mech.math.msu.su/~iliagri/zip/sem2book.pdf
Время работы
Так как на каждой итерации мы считаем одно значение функции и уменьшаем область поиска в раз, пока , то время работы алгоритма составит .
Если удельный вес вычисления функции достаточно большой, тогда получим ускорение работы по сравнению с неулучшенным троичным поиском ( против .
За счет этого достигается выигрыш в производительности, т.к. каждый новый отрезок в раз короче предыдущего (против у троичного поиска) и сходится он в быстрее, чем в троичном поиске, соответственно, в раза меньше вычислений.