Префикс-функция — различия между версиями
| Строка 14: | Строка 14: | ||
<tex>\pi</tex>(i) = k | <tex>\pi</tex>(i) = k | ||
} | } | ||
| + | *'''Корректность работы''' | ||
| + | [[Файл:Prefix1.jpg|center]] | ||
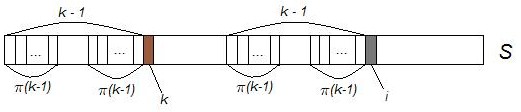
| + | Как видно из рисунка, при совпадении символов <tex>S[k]</tex> и <tex>S[i]</tex> длина наибольшего общего префикса увеличивается на 1. В случае, когда символы <tex>S[k]</tex> и <tex>S[i]</tex> не совпадают, <tex>pi(k-1)</tex> - следующая по максимальности длина потенциального наибольшего общего префикса | ||
| + | |||
*'''Время работы''' | *'''Время работы''' | ||
| − | Сперва отметим очевидный из определения факт: <tex>\pi(k + 1) - \pi(k) \leq 1</tex> для любого <tex>k</tex>. В самом деле, в противном случае <tex>\pi(k)</tex> не максимально. | + | Сперва отметим очевидный из определения факт: <tex>\pi(k + 1) - \pi(k) \leq 1</tex> для любого <tex>k</tex>. В самом деле, в противном случае <tex>\pi(k)</tex> не максимально. |
| − | Теперь рассмотрим произвольную итерацию внешнего цикла <tex>for</tex>. Возможно одно из трёх: | + | Теперь рассмотрим произвольную итерацию внешнего цикла <tex>for</tex>. Возможно одно из трёх: |
| − | + | 1) <tex>s[i] = s[k]</tex>. Тогда значение <tex>k</tex> увеличивается на 1, цикл <tex>while</tex> не итерируется | |
| − | + | 2) <tex>k = 0</tex> <tex>\&</tex> <tex>s[i] \ne s[k]</tex>. Тогда значение <tex>k</tex> не изменяется, цикл <tex>while</tex> не итерируется | |
| − | + | 3) <tex>while</tex> итерируется хотя бы раз. При каждой итерации <tex>while</tex> значение <tex>k</tex> может, очевидно, лишь уменьшаться, при этом, в силу отмеченного выше очевидного наблюдения, общее число итераций <tex>while</tex> для всех итераций <tex>for</tex> не превышает <tex>n</tex> | |
| − | Таким образом, общее время работы - <tex>O(n)</tex>. | + | Таким образом, общее время работы - <tex>O(n)</tex>. |
Версия 20:24, 27 июня 2011
Определение
Префикс-функцией цепочки называется функция
Алгоритм вычисления
- Псевдокод
k = 0 (0) = 0 for (i = 1 .. (n - 1)) { while (k > 0 && s[i] s[k]) k = (k - 1) if (s[i] == s[k]) k = k + 1 (i) = k }
- Корректность работы
Как видно из рисунка, при совпадении символов и длина наибольшего общего префикса увеличивается на 1. В случае, когда символы и не совпадают, - следующая по максимальности длина потенциального наибольшего общего префикса
- Время работы
Сперва отметим очевидный из определения факт: для любого . В самом деле, в противном случае не максимально. Теперь рассмотрим произвольную итерацию внешнего цикла . Возможно одно из трёх: 1) . Тогда значение увеличивается на 1, цикл не итерируется 2) . Тогда значение не изменяется, цикл не итерируется 3) итерируется хотя бы раз. При каждой итерации значение может, очевидно, лишь уменьшаться, при этом, в силу отмеченного выше очевидного наблюдения, общее число итераций для всех итераций не превышает Таким образом, общее время работы - .