Алгоритм Флойда — различия между версиями
AVasilyev (обсуждение | вклад) |
AVasilyev (обсуждение | вклад) |
||
| Строка 30: | Строка 30: | ||
=== Код (окончательный) === | === Код (окончательный) === | ||
| − | Утверждается, что можно избавиться от одной размерности в массиве <tex> d </tex>, т.е. использовать двумерный массив <tex>d_{uv}</tex>. В процессе работы алгоритма поддерживается инвариант <tex>\rho(u, v) \le d_{uv} \le d_{uv}^i</tex>, а | + | Утверждается, что можно избавиться от одной размерности в массиве <tex> d </tex>, т.е. использовать двумерный массив <tex>d_{uv}</tex>. В процессе работы алгоритма поддерживается инвариант <tex>\rho(u, v) \le d_{uv} \le d_{uv}^{(i)}</tex>, а, поскольку, после выполнения работы алгоритма <tex> \rho(u, v) == d_{uv}^{(i)} </tex>, то тогда будет выполняться и <tex> \rho(u, v) == d_{uv} </tex>. |
| + | |||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | В течение работы алгоритма Флойда выполняются неравенства: <tex>\rho(u, v) \le d_{uv} \le d_{uv}^{(i)}</tex>. | ||
| + | |proof= | ||
| + | |||
| + | После инициализации все неравенства, очевидно, выполняются. Далее, массив <tex> d </tex> может измениться только в строчке 5. Докажем оба неравенства по индукции по итерациям алгоритма: | ||
| + | |||
| + | # <tex> \rho(u, v) \le d_{uv} </tex>. Рассмотрим два случая: | ||
| + | #* Значение <tex> d_{uv} </tex> изменилось. Тогда <tex> d_{uv} = d_{ui} + d_{iv} \ge \rho(u, i) + \rho(i, v) \ge \rho(u, v) </tex> (по индукционному предположению и неравенству треугольника для <tex> \rho </tex>). | ||
| + | #* Значение <tex> d_{uv} </tex> не изменилось. Тогда неравенство выполняется автоматически по индукционному предположению. | ||
| + | # <tex> d_{uv} \le d_{uv}^{(i)} </tex>. Аналогично рассмотрим два случая: | ||
| + | #* Значение <tex> d_{uv}^{(i)} </tex> изменилось. Тогда <tex> d_{uv}^{(i)} \ge d_{ui}^{(i-1)} + d_{iv}^{(i-1)} \ge d_{ui}^{(i)} + d_{iv}^{(i)} \ge d_{ui} + d_{uv} \ge d_{uv} </tex>, по индукционному предположению и тому факту, что <tex> d_{uv}^{(i)} </tex> невозрастает с ростом <tex> i </tex>. | ||
| + | #* В ином случае всё очевидно: <tex> d_{uv}^{(i)} = d_{uv}^{(i - 1)} \ge d_{uv} </tex>, и неравенство тривиально. | ||
| + | |||
| + | }} | ||
# Инициализация | # Инициализация | ||
| − | d = w | + | <tex dpi = "105"> d = w </tex> |
# Основная часть | # Основная часть | ||
for i in {1..n}: | for i in {1..n}: | ||
for u in {1..n}: | for u in {1..n}: | ||
for v in {1..n}: | for v in {1..n}: | ||
| − | + | <tex dpi = "105"> d_{uv} = min(d_{uv}, d_{ui} + d_{iv}) </tex> | |
| − | + | Данная реализация работает за время <tex> \Theta(n^3) </tex>, но требует уже <tex> \Theta(n^2) </tex> памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении <tex> \Theta </tex> весьма мала. | |
=== Пример работы === | === Пример работы === | ||
| Строка 81: | Строка 97: | ||
== Вывод кратчайшего пути == | == Вывод кратчайшего пути == | ||
| − | Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив <tex> | + | Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив <tex>next_{uv}</tex>, в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из <tex>u</tex> в <tex>v</tex> по кратчайшему пути. |
=== Модифицированный алгоритм === | === Модифицированный алгоритм === | ||
| Строка 94: | Строка 110: | ||
if (d[u][i] + d[i][v]) < d[u][v]: | if (d[u][i] + d[i][v]) < d[u][v]: | ||
d[u][v] = d[u][i] + d[i][v] | d[u][v] = d[u][i] + d[i][v] | ||
| − | + | next[u][v] = next[u][i] | |
# Вывод кратчайшего пути | # Вывод кратчайшего пути | ||
| Строка 102: | Строка 118: | ||
c = u | c = u | ||
while c != v: | while c != v: | ||
| − | + | print c | |
| − | c = | + | c = next[c][v] |
| − | + | print v | |
[[Файл:Floyd_path.png]] | [[Файл:Floyd_path.png]] | ||
Версия 04:30, 1 ноября 2011
Алгоритм Флойда (алгоритм Флойда–Уоршелла) — алгоритм нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а в случае, когда такой цикл есть, позволяет найти хотя бы один такой цикл. Этот алгоритм работает в течение времени и использует памяти. Разработан в 1962 году.
Содержание
Алгоритм
Постановка задачи
Дан взвешенный ориентированный граф ; , в котором вершины пронумерованы от до . Требуется найти матрицу кратчайших расстояний , в которой элемент либо равен длине кратчайшего пути из в , либо равен , если вершина не достижима из .
Описание
Обозначим длину кратчайшего пути между вершинами и , содержащего, помимо и , только вершины из множества как , .
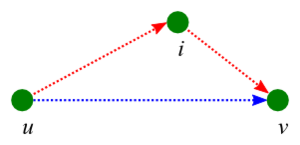
На каждом шаге алгоритма, мы будем брать очередную вершину (пусть её номер — ) и для всех пар вершин и вычислять . То есть, если кратчайший путь из в , содержащий только вершины из множества , проходит через вершину , то кратчайшим путем из в является кратчайший путь из в , объединенный с кратчайшим путем из в . В противном случае, когда этот путь не содержит вершины , кратчайший путь из в , содержащий только вершины из множества является кратчайшим путем из в , содержащим только вершины из множества .
Код (в первом приближении)
# Инициализация # Основная часть for i in {1..n}: for u in {1..n}: for v in {1..n}:
В итоге получаем, что матрица и является искомой матрицей кратчайших путей, поскольку содержит в себе длины кратчайших путей между всеми парами вершин, имеющих в качестве промежуточных вершин вершины из множества , что есть попросту все вершины графа. Такая реализация работает за времени и использует памяти.
Код (окончательный)
Утверждается, что можно избавиться от одной размерности в массиве , т.е. использовать двумерный массив . В процессе работы алгоритма поддерживается инвариант , а, поскольку, после выполнения работы алгоритма , то тогда будет выполняться и .
| Утверждение: |
В течение работы алгоритма Флойда выполняются неравенства: . |
|
После инициализации все неравенства, очевидно, выполняются. Далее, массив может измениться только в строчке 5. Докажем оба неравенства по индукции по итерациям алгоритма:
|
# Инициализация # Основная часть for i in {1..n}: for u in {1..n}: for v in {1..n}:
Данная реализация работает за время , но требует уже памяти. В целом, алгоритм Флойда очень прост, и, поскольку в нем используются только простые операции, константа, скрытая в определении весьма мала.
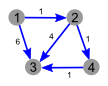
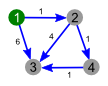
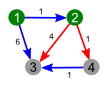
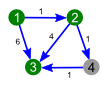
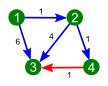
Пример работы
 |
 |
 |
 |
|
Вывод кратчайшего пути
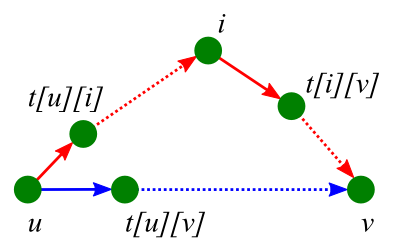
Алгоритм Флойда легко модифицировать таким образом, чтобы он возвращал не только длину кратчайшего пути, но и сам путь. Для этого достаточно завести дополнительный массив , в котором будет храниться номер вершины, в которую надо пойти следующей, чтобы дойти из в по кратчайшему пути.
Модифицированный алгоритм
# Инициализация
d = w
t[u][v] = v если есть ребро uv
# Основная часть
for i in {1..n}:
for u in {1..n}:
for v in {1..n}:
if (d[u][i] + d[i][v]) < d[u][v]:
d[u][v] = d[u][i] + d[i][v]
next[u][v] = next[u][i]
# Вывод кратчайшего пути
def get_shortest_path(u, v):
if d[u][v] == inf:
raise NoPath # Из u в v пути нет
c = u
while c != v:
print c
c = next[c][v]
print v
Литература
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)