Конфигурация

<wikitex>

Эта статья находится в разработке!

Общие определения(R^d)

Определение:

Гиперплоскостью(англ. hyperplane) в $\mathbb{R}^d$ называется его подпространство размерности $\mathbb{R}^{d - 1}$.

Определение:

Конфигурацией(англ. arrangement) $\mathcal{A}(\mathcal{H})$ называется разбиение $\mathbb{R}^d$ в связные открытые(топологически) ячейки размерностей $0, 1 \dots d $ множеством $\mathcal{H}$ гиперплоскостей в $ \mathbb{R}^d$.

Определение:

Ячейкой(англ. cell) размерности $d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в $R^d$, не пересекаемая ни одной гиперплоскостью в $\mathcal{H}$. Ячейкой размерности $k$, где $0 \le k < d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в пересечении гиперплоскостей подмножества $\mathcal{S} \in \mathcal{H}$, которая не пересекается ни одной гиперплоскостью из множества $\mathcal{H} \setminus \mathcal{S}$. TODO: БИДА, сложно обобщить на ограниченные гиперплоскости, спросить у Ковалёва

Определение:

Вершина(англ. vertex) — ячейка размерности 0. Ребро(англ. edge) — ячейка размерности 1. Грань(англ. face) — ячейка размерности 2. Сторона(англ. facet) — ячейка размерности d-1.

Обобщения

В общем случае, не обязательно требовать, чтобы $\mathcal{S}$ было множеством гиперплоскостей. Накладывая некоторые ограничения на поверхности( TODO: возможно, лучше употребить термин «гиперповерхности», но в англ. литературе это surfaces), можно также добиться корректных конфигураций.

К примеру, в $\mathbb{R}^2$ вместо линий(гиперплоскости в $\mathbb{R}^2$) можно брать монотонные по x(то есть каждая параллельная оси y линия пересекает её не более, чем в 1 точке) Жордановы дуги(англ. x-monotonic Jordan arcs), причём такие что максимально количество взаимопересечений каждой пары дуг такого множества — заранее фиксированная константа. Засчёт этого ограничения отсеиваются такие пары дуг как, например, $y = \sin(x)$ и $y = \cos(x)$. А вот пару дуг $y = \cos(x)$ и $y = x^2$ можно взять.

Плоскость(R^2)

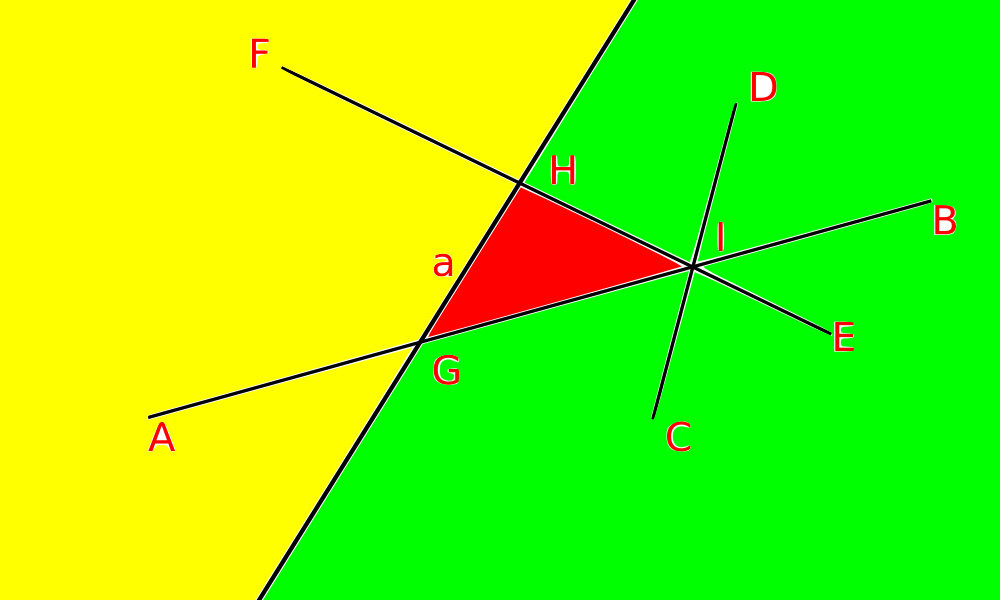
Разрешим ограничивать гиперплоскости — то есть введём лучи и отрезки. Тогда ячейками размерности 0 также считаются точки, ограничивающие их.

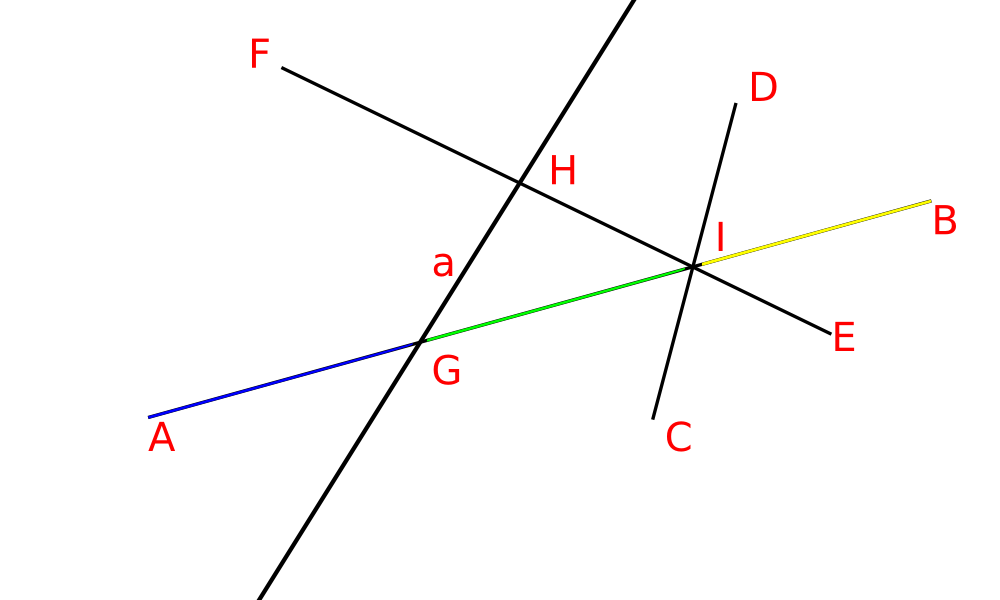
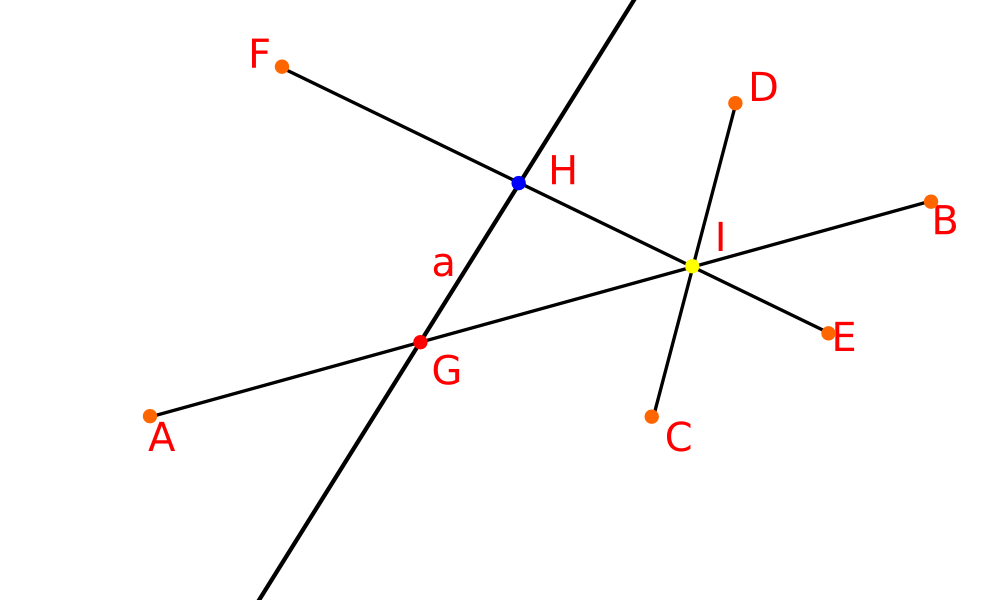
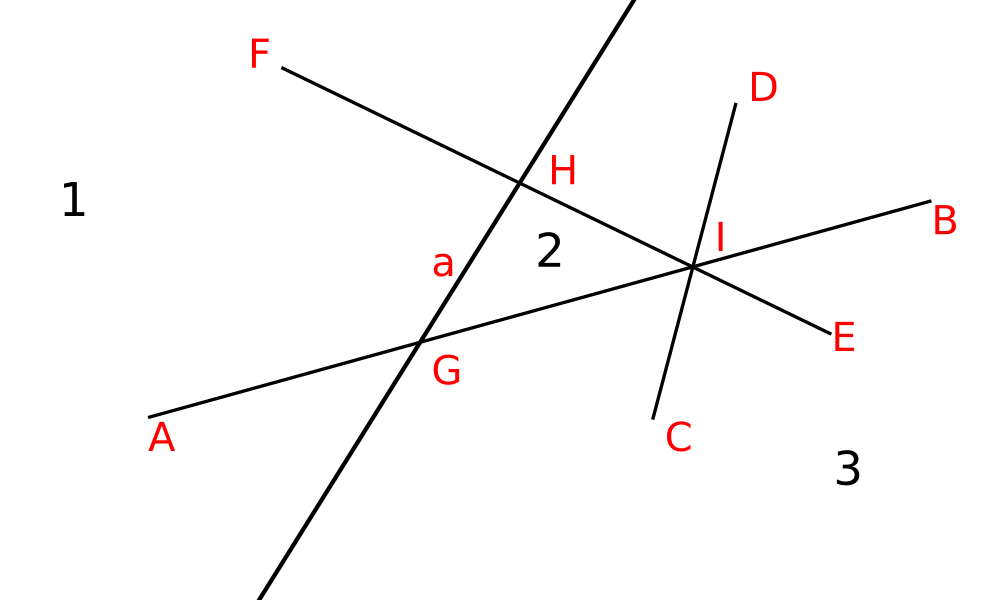
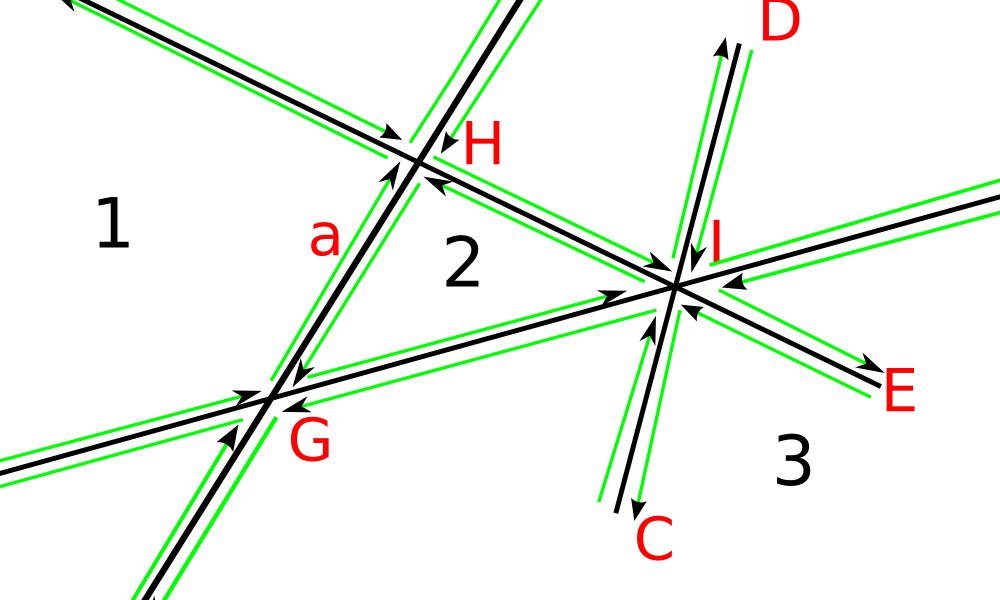
Пример

Возьмём $\mathcal{H} = \{AB, CD, EF, a\}$.

Цветами выделены ячейки размерности 2. Жёлтая и зелёная ячейки не ограничены, красная — ограничена.

Взяв множество S с единственным отрезком AB, получим три ячейки размерности 1. Взяв за множество S поочерёдно CD, EF и a, получим остальные ячейки размерности 1.

Взяв поочерёдно за множество S множества {a, EF}, {a, AB}, {AB, CD, EF}, получим ячейки G, H и I размерности 0. Как было замечено, точки A, B, C, D, E, F — также ячейки размерности 0 как органичивающие отрезки.

Представления конфигураций

Определение:

Пусть $c_1$ - ячейка размерности $k_1$, а $c_2$ — ячейка размерности $k_2$ в конфигурации $\mathcal{A}(\mathcal{S})$. Если $k_2 = k_1 + 1$ и $c_1$ ограничивает $c_2$, то $c_1$ — подъячейка(англ. subcell) $c_2$, а $c_2$ — надъячейка(англ. supercell) $c_1$. Если $c_1$ — подъячейка или надъячейка для $c_2$, то говорят что они смежны(англ. incident).

Иногда удобно вводить ячейку размерности -1 — она является подъячейкой любой ячейки размерности 0, и ячейку размерности d+1 — она является надъячейкой любой ячейки размерности d.

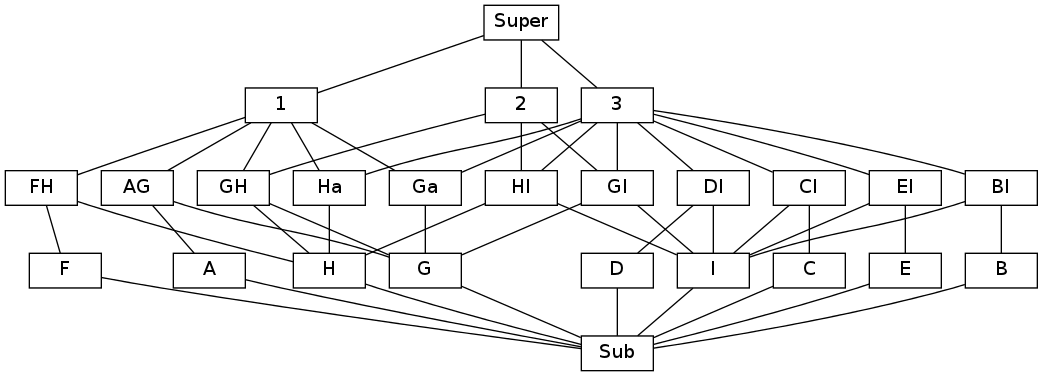
Граф смежности

Граф смежности(англ. incidence graph) конфигурации $\mathcal{A}(\mathcal{S})$ — граф, в котором множество вершин состоит из всех ячеек(в том числе и ячейки размерности -1 и d+1), а ребро между вершинами существует если ячейки, им соответствующие, смежны. Для конфигурации $n$ гиперплоскостей в пространстве $\mathbb{R}^n$ оценкой на количество вершин является $O(n^d)$.

Пример

Пример конфигурации. Номерами обозначены ячейки размерности 2.

Граф смежности для этой конфигурации. Ячейка Super — ячейка размерности d+1, Sub — размерности -1

Скелет

Скелетом(англ. skeleton) называется множество всех вершин и рёбер в конфигурации. Естественным образом он представляется в виде графа. Он позволяет пройтись по всей конфигурации.( TODO: вроде больше ничего полезного).

Пример

В качестве примера выделить второй и третий снизу слои графа из примера для графа смежности.

РСДС(R^2)

Заметим, что на плоскости можно выделить определённый порядок обхода рёбер и позже использовать эту информацию. Граф смежности же не учитывает порядок рёбер и направление. Для того, чтобы поддерживать этот порядок, используется рёберный список двойной связности, РСДС(англ. doubly-connecned edge list, DCEL).

РСДС можно обобщить в cell-tuple structure для произвольной размерности. Она позволяет относительно просто представить информацию о смежности ячеек и порядке обхода конфигурации. Также для $\mathbb{R}^3$ существует похожая структура данных Quad-edge

Представление

Для удобства каждое ребро разбивается на два ориентированных полуребра(half-edges). Каждое полуребро принадлежит только одной грани — той, которая окажется слева если идти по направлению полуребра(т.е. при обходе грани против часовой стрелки). РСДС в общем случае содержит запись о каждой грани, полуребре и вершине конфигурации. Рассмотрим каждый список в отдельности:

1. Список граней содержит данные о грани(например, номер) и указатель на произвольное полуребро, принадлежащее ей.
2. Список полурёбер содержит данные о полуребре, его близнеце(twin edge) — противоположном направленному полуребру(оно не всегда существует, если его нет, будем хранить null), следующем(next) и предыдущем(previous) полуребру в порядке обхода грани, указатели на вершины начала(origin) и конца(destination) и соответствующую ему грань.
3. Список вершин содержит данные о вершине, её координаты и указатель на любое полуребро с началом в ней.

С помощью такого списка можно за линейное время находить все рёбра, ограничивающие данную грань в порядке обхода против часовой стрелки и получить координаты вершин, ограничивающих её.

Стоит заметить, что если нам не нужна дополнительная информация о гранях и вершинах, можно и вовсе не строить таблицы для них.

Пример

Пример конфигурации. Номерами обозначены грани.

Стрелками обозначены полурёбра.

Построим часть РСДС для данной конфигурации.

Список граней Грань Полуребро 1 GH 2 IH 3 EI

Список полурёбер Полуребро Близнец Следующее Предыдущее Начало Конец Грань … … … … … … … GI IG IH HG G I 2 … … … … … … … IC null CI EI I C 3 … … … … … … …

Список вершин Вершина Координаты Полуребро … … … H … HI C … CI … … …

Источники

• Goodman J.E., O'Rourke J. Handbook of discrete and computational geometry. p. 537, 2004, 2nd edition.
• Wikipedia — Doubly connected edge list

</wikitex>