Существенно неоднозначные языки — различия между версиями
(→Неоднозначные грамматики) |
(→Существенно неоднозначные языки) |
||
| Строка 21: | Строка 21: | ||
Возьмем k и рассмотрим слово <tex>0^k 1^k 2^{k+k!}</tex>. | Возьмем k и рассмотрим слово <tex>0^k 1^k 2^{k+k!}</tex>. | ||
| − | Пометим первые k нулей, по [[Лемма Огдена|лемме Огдена]] данное слово можно разбить на 5 частей: <tex>0^k1^k2^{k+k!}= | + | Пометим первые k нулей, по [[Лемма Огдена|лемме Огдена]] данное слово можно разбить на 5 частей: <tex>0^k1^k2^{k+k!}=uvxнz</tex>. |
Понятно, что <tex>v</tex> состоит полностью из нулей, а <tex>x</tex> состоит полностью из единиц, а также длины <tex>v</tex> и <tex>x</tex> равны, так как иначе при накачке мы можем получить слово, не принадлежащее языку. | Понятно, что <tex>v</tex> состоит полностью из нулей, а <tex>x</tex> состоит полностью из единиц, а также длины <tex>v</tex> и <tex>x</tex> равны, так как иначе при накачке мы можем получить слово, не принадлежащее языку. | ||
| Строка 29: | Строка 29: | ||
[[Файл:tree2.png]] | [[Файл:tree2.png]] | ||
| − | Теперь рассмотрим слово <tex>0^{k+k!} 1^k 2^k</tex>, в котором отмечены все двойки. Аналогичными рассуждениями мы получаем, что слово <tex>q</tex> принадлежит языку, а также существует нетерминал <tex>B<tex> такой, что с помощью него можно породить слово <tex>q</tex>. | + | Теперь рассмотрим слово <tex>0^{k+k!} 1^k 2^k</tex>, в котором отмечены все двойки. Аналогичными рассуждениями мы получаем, что слово <tex>q</tex> принадлежит языку, а также существует нетерминал <tex>B</tex> такой, что с помощью него можно породить слово <tex>q</tex>. |
[[Файл:tree3.png]] | [[Файл:tree3.png]] | ||
Версия 19:35, 22 ноября 2011
Неоднозначные грамматики
Неоднозначной грамматикой называется грамматика, которая может породить некоторое слово более чем одним способом (то есть для строки есть более одного дерева разбора).
Пример:
Рассмотрим грамматику и выводимое слово . Его можно вывести двумя способами:
Эта грамматика неоднозначна.
Существенно неоднозначные языки
Язык называется существенно неоднозначным, если он может быть порождён только неоднозначными грамматиками.
Пример такого языка: , где либо , либо
Докажем, что для любой грамматики имеет хотя бы 2 дерева разбора в грамматике .
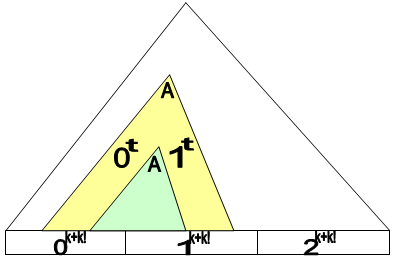
Возьмем k и рассмотрим слово .
Пометим первые k нулей, по лемме Огдена данное слово можно разбить на 5 частей: .
Понятно, что состоит полностью из нулей, а состоит полностью из единиц, а также длины и равны, так как иначе при накачке мы можем получить слово, не принадлежащее языку.
Пусть , тогда возьмём слово . По лемме Огдена слово принадлежит языку, а также существует нетерминал такой, что с помощью него можно породить слово .
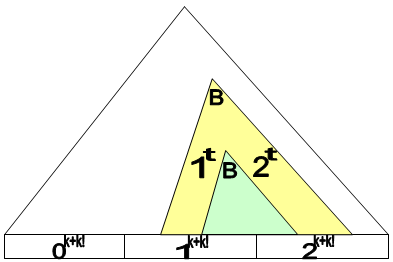
Теперь рассмотрим слово , в котором отмечены все двойки. Аналогичными рассуждениями мы получаем, что слово принадлежит языку, а также существует нетерминал такой, что с помощью него можно породить слово .
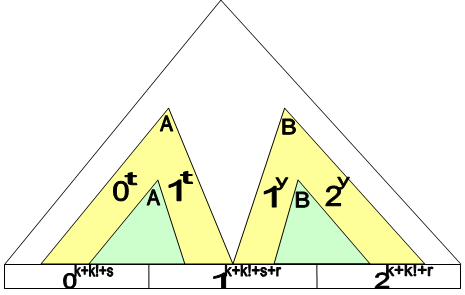
Очевидно, что поддеревья, соответствующие и - разные деревья и одно не является потомком другого.
Пусть в этих двух случай дерево разбора было одно и тоже, то оно порождает слово вида , которое не принадлежит языку.
В результате мы имеем 2 дерева разбора для одного слова. Значит язык существенно не однозначен.