Лемма Огдена — различия между версиями
Rost (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Для каждой [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно-свободный грамматики]] <tex>\Gamma =\langle \Sigma, N, S \in N, P \subset N^{+}\times (\Sigma\cup N)^{*}\rangle</tex> существует такое <tex>n</tex>, что для любого слова <tex>\omega \in L(\Gamma)</tex>, длины не менее <tex>n</tex>, и для любых выделенных в <tex>\omega</tex> не менее <tex>n</tex> позиций | + | Для каждой [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно-свободный грамматики]] <tex>\Gamma =\langle \Sigma, N, S \in N, P \subset N^{+}\times (\Sigma\cup N)^{*}\rangle</tex> существует такое <tex>n</tex>, что для любого слова <tex>\omega \in L(\Gamma)</tex>, длины не менее <tex>n</tex>, и для любых выделенных в <tex>\omega</tex> не менее <tex>n</tex> позиций <tex>\omega</tex> может быть представлено в виде <tex>\omega=uvxyz</tex>, причем: |
| − | # x содержит выделенную позицию | + | # <tex>x</tex> содержит выделенную позицию |
# либо <tex>u</tex> и <tex>v</tex>, либо <tex>y</tex> и <tex>z</tex> обе содержат выделенные позиции; | # либо <tex>u</tex> и <tex>v</tex>, либо <tex>y</tex> и <tex>z</tex> обе содержат выделенные позиции; | ||
# <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций; | # <tex>vxy</tex> содержат не более <tex>n</tex> выделенных позиций; | ||
| Строка 11: | Строка 11: | ||
Пусть <tex>v_1</tex> — корень <tex>T</tex>, а <tex>v_{i + 1}</tex> — сын <tex>v_i</tex>, который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то <tex>v_{i + 1}</tex> самый правый из них). Рассмотрим <tex>v_1, v_2, ..., v_p</tex> — путь от корня до листа. | Пусть <tex>v_1</tex> — корень <tex>T</tex>, а <tex>v_{i + 1}</tex> — сын <tex>v_i</tex>, который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то <tex>v_{i + 1}</tex> самый правый из них). Рассмотрим <tex>v_1, v_2, ..., v_p</tex> — путь от корня до листа. | ||
| − | Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. | + | Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Докажем по индукции, что если среди <tex>v_1, v_2, ..., v_i</tex> вершин есть <tex>k</tex> ветвящихся, то <tex>v_{i + 1}</tex> имеет хотя бы <tex>l^{2m + 3 - k}</tex> выделенных потомков. <br>База индукции: <tex>i = 0</tex>. Тогда <tex>k = 0</tex> и <tex>v_1</tex> имеет по крайне мере <tex>n</tex> выделенных потомков, поскольку является корнем. <br>Индукционный переход. Если <tex>v_i</tex> не является ветвящейся вершиной, то <tex>v_{i + 1}</tex> имеет такое же число ветвящихся потомков как и <tex>v_i</tex>. Если <tex>v_i</tex> — ветвящаяся вершина, то <tex>v_{i + 1}</tex> имеет не более чем в <tex>l</tex> раз меньшее число выделенных потомков. |
Поскольку <tex>v_1</tex> имеет хотя бы <tex>n = l^{2m + 3}</tex> выделенных потомков, то <tex>v_1, v_2, ..., v_p</tex> содержит по крайне мере <tex>2m + 3</tex> ветвящиеся вершин. Заметим, что <tex>v_p</tex> — лист, поэтому <tex>p > 2m + 3</tex>. | Поскольку <tex>v_1</tex> имеет хотя бы <tex>n = l^{2m + 3}</tex> выделенных потомков, то <tex>v_1, v_2, ..., v_p</tex> содержит по крайне мере <tex>2m + 3</tex> ветвящиеся вершин. Заметим, что <tex>v_p</tex> — лист, поэтому <tex>p > 2m + 3</tex>. | ||
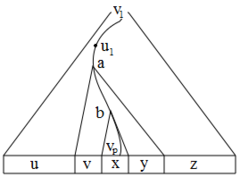
| − | [[Файл:derivation_tree_T.png|240px|thumb|left|Дерево вывода <tex>T</tex>]]Будем называть <tex>v_i</tex> левой ветвящейся вершиной, если ее сын, не принадлежащий пути <tex>v_1, v_2, ..., v_p</tex>, имеет выделенного потомка лежащего слева от <tex>v_p</tex>. В противном случае назовем <tex>v_i</tex> правой ветвящейся вершиной. Рассмотрим последние <tex>2m + 3</tex> вершины | + | [[Файл:derivation_tree_T.png|240px|thumb|left|Дерево вывода <tex>T</tex>]]Будем называть <tex>v_i</tex> левой ветвящейся вершиной, если ее сын, не принадлежащий пути <tex>v_1, v_2, ..., v_p</tex>, имеет выделенного потомка лежащего слева от <tex>v_p</tex>. В противном случае назовем <tex>v_i</tex> правой ветвящейся вершиной. Рассмотрим последние <tex>2m + 3</tex> вершины, принадлежащие пути <tex>v_1, v_2, ..., v_p</tex>. Предположим, что хотя бы <tex>m + 2</tex> вкршины левые ветвящиеся (случай, когда хотя бы <tex>m + 2</tex> вершины правые ветвящиеся, разбирается аналогично). Пусть <tex>u_1, u_2, ..., u_{m + 2}</tex> — последние <tex>m + 2</tex> левые ветвящиеся вершины. Поскольку <tex>m = |N|</tex>, то среди них можно найти как минимум две вершины, соответствующие одному нетерминалу. Обозначим эти вершины <tex>a</tex> и <tex>b</tex>, причем <tex>b</tex> потомок <tex>a</tex>. Тогда на рисунке показано как представить <tex>\omega</tex> в требуемом виде. |
| − | Условие (1) выполнено, поскольку <tex>x</tex> содержит выделенную вершину, а именно <tex>v_p</tex>. Очевидно, что условие(4) выполнено в силу предложенного разбиения <tex>\omega</tex>. Кроме того, <tex>u</tex> содержит выделенную вершину, а именно потомка некоторого сына вершины <tex>u_1</tex>. Аналогично выделенный потомок некоторого сына вершины <tex>a</tex> содержится в <tex>v</tex>. Таким образом, условие (2) выполнено. Поскольку между <tex>v_p</tex> и <tex>a</tex> не более <tex>2m + 3</tex> вершин, то вершина <tex>a</tex> имеет не более <tex>n</tex> выделенных потомков, поэтому условие (3) выполнено. | + | Условие (1) выполнено, поскольку <tex>x</tex> содержит выделенную вершину, а именно <tex>v_p</tex>. Очевидно, что условие (4) выполнено в силу предложенного разбиения <tex>\omega</tex>. Кроме того, <tex>u</tex> содержит выделенную вершину, а именно потомка некоторого сына вершины <tex>u_1</tex>. Аналогично выделенный потомок некоторого сына вершины <tex>a</tex> содержится в <tex>v</tex>. Таким образом, условие (2) выполнено. Поскольку между <tex>v_p</tex> и <tex>a</tex> не более <tex>2m + 3</tex> вершин, то вершина <tex>a</tex> имеет не более <tex>n</tex> выделенных потомков, поэтому условие (3) выполнено. |
}} | }} | ||
Версия 06:46, 9 декабря 2011
| Лемма: |
Для каждой контекстно-свободный грамматики существует такое , что для любого слова , длины не менее , и для любых выделенных в не менее позиций может быть представлено в виде , причем:
|
| Доказательство: |
|
Введем следующие обозначения: и — длина самой длинной правой части правила из . Тогда в качестве возьмем . Рассмотрим дерево разбора для произвольного слова , у которого . В силу выбора в будет по крайне мере один путь от корня до листа длины, не менее . Произвольным образом выделим в не менее позиций. Соответствующие этим позициям листья дерева будем называть выделенными. Пусть — корень , а — сын , который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то самый правый из них). Рассмотрим — путь от корня до листа. Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Докажем по индукции, что если среди вершин есть ветвящихся, то имеет хотя бы выделенных потомков. Поскольку имеет хотя бы выделенных потомков, то содержит по крайне мере ветвящиеся вершин. Заметим, что — лист, поэтому . Будем называть левой ветвящейся вершиной, если ее сын, не принадлежащий пути , имеет выделенного потомка лежащего слева от . В противном случае назовем правой ветвящейся вершиной. Рассмотрим последние вершины, принадлежащие пути . Предположим, что хотя бы вкршины левые ветвящиеся (случай, когда хотя бы вершины правые ветвящиеся, разбирается аналогично). Пусть — последние левые ветвящиеся вершины. Поскольку , то среди них можно найти как минимум две вершины, соответствующие одному нетерминалу. Обозначим эти вершины и , причем потомок . Тогда на рисунке показано как представить в требуемом виде.
|