Реализация вычитания сумматором — различия между версиями
Alex z (обсуждение | вклад) |
Alex z (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Что бы реализовать вычитание [[Каскадный сумматор|каскадным]] или [[Двоичный каскадный сумматор|двоичным каскадным сумматором]], нужно сложить на нём уменьшаемое с противоположным по знаку вычитаемым, так же как и при вычитании обычных чисел. Тогда полученная сумма будет разностью данных чисел. | Что бы реализовать вычитание [[Каскадный сумматор|каскадным]] или [[Двоичный каскадный сумматор|двоичным каскадным сумматором]], нужно сложить на нём уменьшаемое с противоположным по знаку вычитаемым, так же как и при вычитании обычных чисел. Тогда полученная сумма будет разностью данных чисел. | ||
| − | <tex> \large x - y = x +(-y)</tex> | + | <tex> \large x - y = x + (-y)</tex> |
Инверсия знака записанного в двоичном виде числа происходит точно так же, как и в [[Представление целых чисел: прямой код, код со сдвигом, дополнительный код#Дополнительный код|дополнительном коде]]. | Инверсия знака записанного в двоичном виде числа происходит точно так же, как и в [[Представление целых чисел: прямой код, код со сдвигом, дополнительный код#Дополнительный код|дополнительном коде]]. | ||
| Строка 52: | Строка 52: | ||
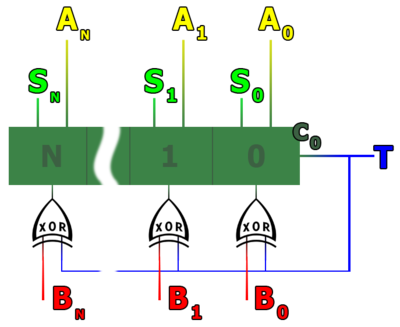
!<math> \mathbf {\color{Blue}T} </math> | !<math> \mathbf {\color{Blue}T} </math> | ||
|бит отвечающий за знак операции | |бит отвечающий за знак операции | ||
| − | + | '''T''' подключён к '''C<small>0</small>''' | |
| − | '''T''' подключён к '''C<small>0</small>''' | ||
|<center>'''0''' если <tex> \large S = A + B</tex><br />'''1''' если <tex> \large S = A - B</tex></center> | |<center>'''0''' если <tex> \large S = A + B</tex><br />'''1''' если <tex> \large S = A - B</tex></center> | ||
|- | |- | ||
| Строка 59: | Строка 58: | ||
|[[Сумматор|блоки]] [[Каскадный сумматор|каскадного]] или [[Двоичный каскадный сумматор|двоичного каскадного]] сумматора | |[[Сумматор|блоки]] [[Каскадный сумматор|каскадного]] или [[Двоичный каскадный сумматор|двоичного каскадного]] сумматора | ||
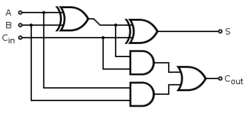
|[[Файл:Full_Adder.png|250px|Блок сумматор]] | |[[Файл:Full_Adder.png|250px|Блок сумматор]] | ||
| + | |- | ||
| + | !<math> \mathbf {\color{Black}\mbox{C}_\mathrm{0}} </math> | ||
| + | |Изначально ненужный бит в сумматоре, | ||
| + | однако он [[Реализация вычитания сумматором#Оптимизация|полезен при вычитании]]. | ||
| + | | | ||
| + | В последующих блоках | ||
| + | в бит переноса подаётся | ||
| + | старший разряд | ||
| + | предыдущего суммирования. | ||
|} | |} | ||
|[[Файл:Arithmometer_SUM_SUB.png|400px|Арифмометр]] | |[[Файл:Arithmometer_SUM_SUB.png|400px|Арифмометр]] | ||
Версия 20:44, 22 декабря 2011
Содержание
Преобразование чисел для вычитания сумматором
Что бы реализовать вычитание каскадным или двоичным каскадным сумматором, нужно сложить на нём уменьшаемое с противоположным по знаку вычитаемым, так же как и при вычитании обычных чисел. Тогда полученная сумма будет разностью данных чисел.
Инверсия знака записанного в двоичном виде числа происходит точно так же, как и в дополнительном коде.
Данное число нужно инвертировать и прибавить к нему единицу.
Например число будет записано как , так как , а
Оптимизация
Очевидно, что такой подход к вычитанию сумматором не оптимален, так как придётся вносить в схему последовательно 2 сумматора или блок памяти, для запоминания промежуточных действий таких как, сложение с единицей. Что бы упростить вычисления нужно воспользоваться лишним битом переноса в сумматоре, в который посылают ноль, и послать в него единицу при вычитании и ноль при суммировании. Вместо того что бы инвертировать вычитаемое число, можно сделать XOR бита первого переноса с каждым битом вычитаемого числа. Таким образом, можно посылать в полученный арифмометр числа точно так же как и при сложении, только первый бит переноса будет отвечать за знак операции: 0-сложение 1-вычитание.
Пример реализации вычитания сумматором
| Условные обозначения | Изображение арифмометра | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|