Эргодическая марковская цепь — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Эргодическая''' [Марковская цепь|марковская цепь]] {{---}} марковская цепь, целиком состоящая из одного эргодического класса. | + | '''Эргодическая''' [[Марковская цепь|марковская цепь]] {{---}} марковская цепь, целиком состоящая из одного эргодического класса. |
}} | }} | ||
Версия 05:40, 17 января 2012
| Определение: |
| Эргодическая марковская цепь — марковская цепь, целиком состоящая из одного эргодического класса. |
Эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (цикл) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают.
называется эргодической, если существует дискретное распределение (называемое эргодическим) , такое что и
- (вероятность оказаться в -ом состоянии, выйдя из -ого, через переходов).
Содержание
Стационарный режим
Эргодические марковские цепи описываются сильно связным графом. Это означает, что в такой системе возможен переход из любого состояния в любое состояние за конечное число шагов.
Для эргодических цепей при достаточно большом времени функционирования () наступает стационарный режим, при котором вероятности состояний системы не зависят от времени и не зависят от распределения вероятностей в начальный момент времени, т.е. .
Для определения стационарных вероятностей нахождения системы в состоянии нужно составить систему линейных однородных алгебраических уравнений с неизвестными:
, где
Можно заметить, что так как все свободные члены равны нулю, система имеет бесконечное число решений. Однако, у нас есть дополнительные условия на решение: и . Следующая теорема утверждает единственность решения такой системы.
Основная теорема об эргодических распределениях
| Теорема (Основная теорема об эргодических распределениях): |
Пусть - цепь Маркова с дискретным пространством состояний и матрицей переходных вероятностей . Тогда эта цепь является эргодической тогда и только тогда, когда она
Эргодическое распределение тогда является единственным решением системы:
|
Пример
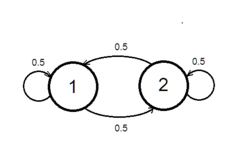
Рассмотрим эксперимент по бросанию честной монеты. Тогда соответствующая этому эксперименту марковская цепь будет иметь 2 состояния. Состояние меняется на противоположное, при бросании монеты, с вероятностью .
Рассмотрим матрицу, следующего вида: . Такая матрица является стохастической, а, значит, корректно определяет марковскую цепь. Такая цепь является эргодической, так как существует эргодическое распределение , такое что .
Примечания
- ↑
Пусть — цепь Маркова с тремя состояниями , и её матрица переходных вероятностей имеет вид
Ссылки
Литература
Дж. Кемени, Дж. Снелл "Конечные цепи Маркова" - Издательство "Наука", 1970 г - 129 c.