Трапецоидная карта — различия между версиями
Shagal (обсуждение | вклад) |
|||
| Строка 4: | Строка 4: | ||
Мы можем найти по карте наше местоположение и сказать в какой области мы находимся. | Мы можем найти по карте наше местоположение и сказать в какой области мы находимся. | ||
| + | Области задаются отрезками. | ||
| − | + | '''Формальная постановка задачи''' | |
| − | + | Есть множество отрезков на плоскости. | |
| + | Есть запрос (точка q), на выход подается область заданная какими-то отрезками в которой находится q. | ||
| + | |||
| + | ==Структура данных== | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | + | *''Геометрическая'' | |
| − | + | У нас есть множество отрезков ограничееных оболочкой R(это не выпуклая оболочка, а просто мнимая граница плоскости за которую не вылезают отрезки) | |
| − | + | ||
| + | Мы договариваемся что никакие две точки не лежат на одной вертикале(в противном случаи все еще противнее) | ||
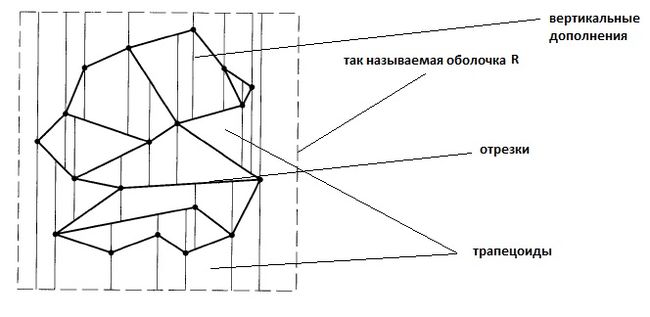
| − | + | ''Трапецоидная карта'' множества отрезков S - это эти отрезки + из кажой точки выпущены два луча, вверх и вниз до первого пересечения с другим отрезком или с оболочкой R. | |
| − | + | {{Лемма | |
| − | + | |statement= Любой face трапецоидной карты ограничен одним или двумя вертикальными отрезками и обязательно двумя не вертикальными отрезками. | |
| − | + | }} | |
| + | [[Файл:Trapazoidmapshagal.jpg|650px|thumb|right|трапецоидная карта]] | ||
| + | |||
Именно отсюда берется название стрктуры, так как любой face либо трапеция, либо треугольник. | Именно отсюда берется название стрктуры, так как любой face либо трапеция, либо треугольник. | ||
| − | Введем обозначения для навигации по карте. | + | |
| − | + | ||
| − | + | Введем обозначения для навигации по карте. | |
| − | + | ||
| − | + | *левая граница(leftp) - точка определяющая левуюы сторону трапецоида или в случаи треугольника просто являющаяся левой вершиной. | |
| + | |||
| + | *правая граница(rightp) - аналогично левой только справа. | ||
| + | |||
| + | *верхний отрезок(top) и нижний отрезок(bottom) - отрезки ограничивающие трапецоид сверху и снизу. | ||
| + | |||
| + | *трапецоиды называются смежными, если имеют общую вертикальную границу. | ||
| + | |||
| + | *пусть <tex>\Delta_1 и \Delta_2</tex> смежны и либо top(<tex>\Delta_1</tex>) = top(<tex>\Delta_2</tex>), либо bottom(<tex>\Delta_1</tex>) = bottom(<tex>\Delta_2</tex>) | ||
| + | Тогда <tex>\Delta_1</tex>,<tex>\Delta_2</tex> называют либо большими левыми соседями, либо меньшими. | ||
| − | + | Хранить трапецоиды можно в чем угодно. Вместе с самим трапецоидом, стоит хранить leftp, rightp, top и bottom так же следует хранить соседей трапецоида. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Версия 21:41, 15 февраля 2012
Трапецоидная карта - геометрическая структура позволяющая локализоваться на площади за .
Постановка задачи
Предположим, у нас есть наши координаты, и есть карта мира. Мы можем найти по карте наше местоположение и сказать в какой области мы находимся. Области задаются отрезками. Формальная постановка задачи Есть множество отрезков на плоскости. Есть запрос (точка q), на выход подается область заданная какими-то отрезками в которой находится q.
Структура данных
- Геометрическая
У нас есть множество отрезков ограничееных оболочкой R(это не выпуклая оболочка, а просто мнимая граница плоскости за которую не вылезают отрезки)
Мы договариваемся что никакие две точки не лежат на одной вертикале(в противном случаи все еще противнее)
Трапецоидная карта множества отрезков S - это эти отрезки + из кажой точки выпущены два луча, вверх и вниз до первого пересечения с другим отрезком или с оболочкой R.
| Лемма: |
Любой face трапецоидной карты ограничен одним или двумя вертикальными отрезками и обязательно двумя не вертикальными отрезками. |
Именно отсюда берется название стрктуры, так как любой face либо трапеция, либо треугольник.
Введем обозначения для навигации по карте.
- левая граница(leftp) - точка определяющая левуюы сторону трапецоида или в случаи треугольника просто являющаяся левой вершиной.
- правая граница(rightp) - аналогично левой только справа.
- верхний отрезок(top) и нижний отрезок(bottom) - отрезки ограничивающие трапецоид сверху и снизу.
- трапецоиды называются смежными, если имеют общую вертикальную границу.
- пусть смежны и либо top() = top(), либо bottom() = bottom()
Тогда , называют либо большими левыми соседями, либо меньшими.
Хранить трапецоиды можно в чем угодно. Вместе с самим трапецоидом, стоит хранить leftp, rightp, top и bottom так же следует хранить соседей трапецоида.