Идеальное хеширование — различия между версиями
(→Поиск) |
|||
| Строка 1: | Строка 1: | ||
| − | '''Двойное хеширование''' {{---}} метод борьбы с возникающими | + | '''Двойное хеширование''' {{---}} метод борьбы с коллизиями, возникающими при [[Открытое_и_закрытое_хеширование#Закрытое хеширование|закрытом хешировании]], основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы. |
==Принцип двойного хеширования== | ==Принцип двойного хеширования== | ||
| − | При двойном хешировании используются две независимые хеш-функции <tex> h_1(k) </tex> и <tex> h_2(k) </tex>. Пусть <tex> k </tex> это наш ключ, <tex> m </tex> размер нашей таблицы, <tex> \mod m </tex> | + | При двойном хешировании используются две независимые хеш-функции <tex> h_1(k) </tex> и <tex> h_2(k) </tex>. Пусть <tex> k </tex> {{---}} это наш ключ, <tex> m </tex> {{---}} размер нашей таблицы, <tex>n \mod m </tex> {{---}} остаток от деления <tex> n </tex> на <tex> m </tex>, тогда сначала исследуется ячейка с адресом <tex> h_1(k) </tex>, если она уже занята, то рассматривается <tex> (h_1(k) + h_2(k)) \mod m </tex>, затем <tex> (h_1(k) + 2 \cdot h_2(k)) \mod m </tex> и так далее. В общем случае идёт проверка последовательности ячеек <tex> (h_1(k) + i \cdot h_2(k)) \mod m </tex> где <tex> i = (0, 1, \; ... \;, m - 1) </tex> |
| + | |||
| + | Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за <tex>O(1)</tex>, в худшем {{---}} за <tex>O(m)</tex>, что не отличается от обычного [[Открытое_и_закрытое_хеширование#Линейное разрешение коллизий|линейного разрешения коллизий]]. | ||
| + | Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной. | ||
| + | |||
| + | <center> | ||
| + | <tex>\forall x \neq y \; \exists h_1,h_2 : \Pr(h_1(x)=h_1(y))> \Pr((h_1(x)=h_1(y))\cap(h_2(x)=h_2(y)))</tex> | ||
| + | </center> | ||
==Выбор хеш-функций== | ==Выбор хеш-функций== | ||
| Строка 37: | Строка 44: | ||
==Простая реализация== | ==Простая реализация== | ||
| − | + | Пусть у нас есть некоторый объект <tex> item </tex>, в котором определено поле <tex> key </tex>, от которого можно вычислить хеш-функции <tex> h_1(key)</tex> и <tex> h_2(key) </tex> | |
| − | Так же у нас есть таблица <tex> table </tex> величиной <tex> m </tex> состоящая из объектов типа <tex> item </tex>. | + | Так же у нас есть таблица <tex> table </tex> величиной <tex> m </tex>, состоящая из объектов типа <tex> item </tex>. |
===Вставка=== | ===Вставка=== | ||
| − | <pre>insert(item) | + | <pre>insert(item) |
x = h1(item.key) | x = h1(item.key) | ||
y = h2(item.key) | y = h2(item.key) | ||
| − | for (i = 0; i < m; i++) | + | for (i = 0; i < m; i++) |
| − | if | + | if table[x] == null |
table[x] = item | table[x] = item | ||
| − | return | + | return |
| − | + | x = (x + y) mod m | |
| − | x = (x + y) mod m | + | table.resize() //ошибка, требуется увеличить размер таблицы</pre> |
| − | |||
| − | |||
| − | |||
===Поиск=== | ===Поиск=== | ||
| − | <pre>search(key) | + | <pre>search(key) |
x = h1(key) | x = h1(key) | ||
y = h2(key) | y = h2(key) | ||
| − | for (i = 0; i < m; i++) | + | for (i = 0; i < m; i++) |
| − | if | + | if table[x] != null |
| − | if | + | if table[x].key == key |
return table[x] | return table[x] | ||
else | else | ||
return null | return null | ||
| − | x = (x + y) mod m | + | x = (x + y) mod m |
| − | + | return null</pre> | |
| − | return null | ||
| − | |||
==Реализация с удалением== | ==Реализация с удалением== | ||
| Строка 74: | Строка 76: | ||
===Вставка=== | ===Вставка=== | ||
| − | <pre>insert(item) | + | <pre>insert(item) |
x = h1(item.key) | x = h1(item.key) | ||
y = h2(item.key) | y = h2(item.key) | ||
| − | for (i = 0; i < m; i++) | + | for (i = 0; i < m; i++) |
| − | if | + | if table[x] == null || deleted[x] |
table[x] = item | table[x] = item | ||
deleted[x] = false | deleted[x] = false | ||
| − | return | + | return |
| − | + | x = (x + y) mod m | |
| − | x = (x + y) mod m | + | table.resize() //ошибка, требуется увеличить размер таблицы</pre> |
| − | |||
| − | |||
| − | |||
===Поиск=== | ===Поиск=== | ||
| − | <pre>search(key) | + | <pre>search(key) |
x = h1(key) | x = h1(key) | ||
y = h2(key) | y = h2(key) | ||
| − | for (i = 0; i < m; i++) | + | for (i = 0; i < m; i++) |
| − | if | + | if table[x] != null |
| − | if | + | if table[x].key == key && !deleted[x] |
return table[x] | return table[x] | ||
else | else | ||
return null | return null | ||
| − | x = (x + y) mod m | + | x = (x + y) mod m |
| − | + | return null</pre> | |
| − | return null | ||
| − | |||
===Удаление=== | ===Удаление=== | ||
| − | <pre>remove(key) | + | <pre>remove(key) |
x = h1(key) | x = h1(key) | ||
y = h2(key) | y = h2(key) | ||
| − | for (i = 0; i < m; i++) | + | for (i = 0; i < m; i++) |
| − | if | + | if table[x] != null |
| − | if | + | if table[x].key == key |
deleted[x] = true | deleted[x] = true | ||
else | else | ||
return | return | ||
| − | x = (x + y) mod m | + | x = (x + y) mod m</pre> |
| − | |||
| − | |||
==См. также== | ==См. также== | ||
Версия 16:48, 7 мая 2012
Двойное хеширование — метод борьбы с коллизиями, возникающими при закрытом хешировании, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.
Содержание
Принцип двойного хеширования
При двойном хешировании используются две независимые хеш-функции и . Пусть — это наш ключ, — размер нашей таблицы, — остаток от деления на , тогда сначала исследуется ячейка с адресом , если она уже занята, то рассматривается , затем и так далее. В общем случае идёт проверка последовательности ячеек где
Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за , в худшем — за , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.
Выбор хеш-функций
может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, должна возвращать значения:
- не равные
- независимые от
- взаимно простые с величиной хеш-таблицы
Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а возвращает натуральные числа, меньшие . Второй — размер таблицы является степенью двойки, а возвращает нечетные значения.
Например, если размер таблицы равен , то в качестве можно использовать функцию вида
Пример
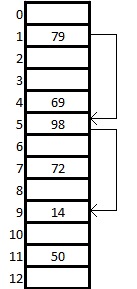
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:
Мы хотим вставить ключ 14. Изначально . Тогда . Но ячейка с индексом 1 занята, поэтому увеличиваем на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При получаем . Ячейка с номером 9 свободна, значит записываем туда наш ключ.
Таким образом, основная особенность двойного хеширования состоит в том, что при различных пара дает различные последовательности ячеек для исследования.
Простая реализация
Пусть у нас есть некоторый объект , в котором определено поле , от которого можно вычислить хеш-функции и
Так же у нас есть таблица величиной , состоящая из объектов типа .
Вставка
insert(item)
x = h1(item.key)
y = h2(item.key)
for (i = 0; i < m; i++)
if table[x] == null
table[x] = item
return
x = (x + y) mod m
table.resize() //ошибка, требуется увеличить размер таблицы
Поиск
search(key)
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++)
if table[x] != null
if table[x].key == key
return table[x]
else
return null
x = (x + y) mod m
return null
Реализация с удалением
Что бы наша хеш-таблица поддерживала удаление, требуется добавить массив типов , равный по величине массиву . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.
Вставка
insert(item)
x = h1(item.key)
y = h2(item.key)
for (i = 0; i < m; i++)
if table[x] == null || deleted[x]
table[x] = item
deleted[x] = false
return
x = (x + y) mod m
table.resize() //ошибка, требуется увеличить размер таблицы
Поиск
search(key)
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++)
if table[x] != null
if table[x].key == key && !deleted[x]
return table[x]
else
return null
x = (x + y) mod m
return null
Удаление
remove(key)
x = h1(key)
y = h2(key)
for (i = 0; i < m; i++)
if table[x] != null
if table[x].key == key
deleted[x] = true
else
return
x = (x + y) mod m
См. также
Литература
- Бакнелл Дж. М. Фундаментальные алгоритмы и структуры данных в Delphi, 2003
- Кнут Д. Э. Искусство программирования, том 3. Сортировка и поиск, 2-е издание, 2000
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение и анализ, 2010
- Седжвик Р. Фундаментальные алгоритмы на C. Части 1-4. Анализ. Структуры данных. Сортировка. Поиск, 2003